高中数学人教A版必修5第三章3.3.1二元一次不等式(组)与平面区域课件(共23张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第三章3.3.1二元一次不等式(组)与平面区域课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 269.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览








文档简介
课件23张PPT。3.3.1 二元一次不等式(组)与平面区域一、引入:一家银行的信贷部计划年初投入25000000元用于企业和个人贷款,希望这笔资金至少可以带来30000元的收益,其中从企业贷款中获益12%,从个人贷款中获益10%,那么信贷部应该如何分配资金呢? 1、建立二元一次不等式模型 (1)把实际问题转化为数学问题: (2)把文字语言转化为符号语言: 资金总数为25000000元 收益为 (3)抽象出数学模型: 选择方式应满足的条件: 设用于企业贷款的资金为x元,用于个人贷款的资金为y元。二、新知探究: 2、二元一次不等式和二元一次不等式组的定义 (1)二元一次不等式: 含有两个未知数,并且未知数的最高次数是1的不等式; (2)二元一次不等式组: 由几个二元一次不等式组成的不等式组; (3)二元一次不等式(组)的解集: 满足二元一次不等式(组)的有序实数对(x,y)构成的集合;(4)二元一次不等式(组)的解集可以看成是直角坐标系内的点构成的集合。 二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 回忆:一元一次不等式(组)的解集所表示的图形
——数轴上的区间。 一元二次不等式的解集——不等式的边界即方程。 思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形? 二、新知探究: (2)探究 特殊:二元一次不等式x – y < 6的解集所表示的图形。 作出x – y = 6的图像——一条直线,
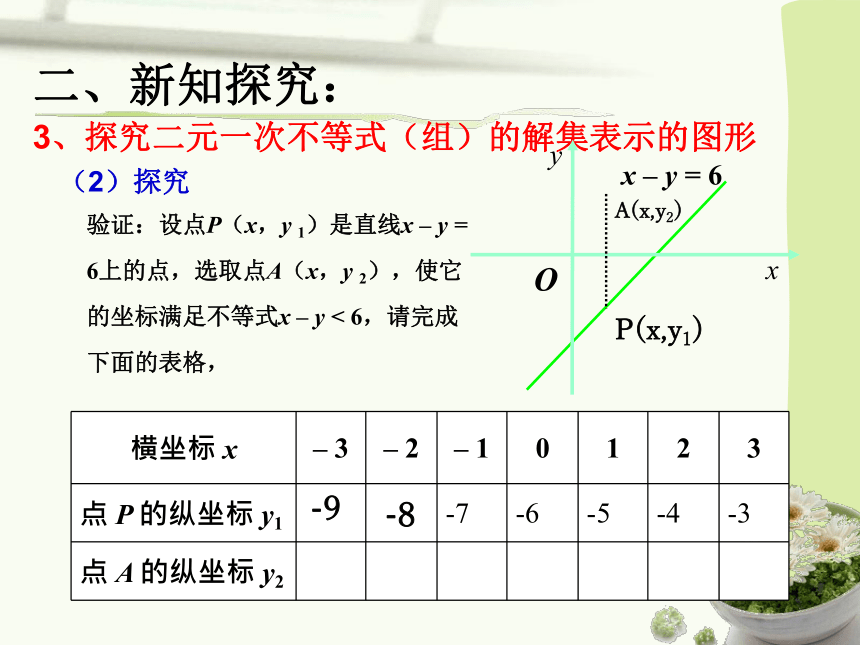
直线把平面分成两部分:左上方区域和右下方区域。 3、探究二元一次不等式(组)的解集表示的图形 左上方区域右下方区域二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 (2)探究 验证:设点P(x,y 1)是直线x – y = 6上的点,选取点A(x,y 2),使它的坐标满足不等式x – y < 6,请完成下面的表格, 二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 结论 在平面直角坐标系中,以二元一次不等式x – y < 6的解为坐标的点都在直线x – y = 6的左上方;反过来,直线x – y = 6左上方的点的坐标都满足不等式x – y < 6。 二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 结论 不等式x – y < 6表示直线x – y = 6左上方的平面区域; 不等式x – y > 6表示直线x – y = 6右下方的平面区域; 直线叫做这两个区域的边界。 二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 从特殊到一般情况: 二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线) 结论一 二元一次不等式表示相应直线的某一侧区域二、新知探究: 4.二元一次不等式表示哪个平面区域的判断方法 直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域,C≠0时,常把原点作为特殊点,C=0时(0,1)(1,0)等。结论二直线定界,特殊点定域。 同侧同号,异侧异号例1:画出不等式 x + 4y < 4表示的平面区域 解:(1)直线定界:先画直线x + 4y – 4 = 0(画成虚线)(2)特殊点定域:取原点(0,0),代入x + 4y - 4,因为 0 + 4×0 – 4 = -4 < 0所以,原点在x + 4y – 4 < 0表示的平面区域内,
不等式x + 4y – 4 < 0表示的区域如图所示。三、例题示范:课堂练习1:(1)画出不等式4x―3y≤12
表示的平面区域(2)画出不等式x≥1
表示的平面区域y < -3x+12
x<2y 的解集。例2、用平面区域表示不等式组解:不等式x-y+5≥0表示
直线x-y+5=0上及右
下方的点的集合,x+y≥0表示直线x+y=0
上及右上方的点的集合,x≤3表示直线x=3上及
左方的点的集合。
x+y=0x-y+5=0x=3所以,不等式所表示的平面区域如图所示35-5x-y+5=0x+y=0x=3变式一:
画出不等式(x+2y+1)(x-y+4)<0
表示的平面区域.变式二:由直线x+y+2=0,x+2y+1=0和
2x+y+1=0围成的三角形(包括边界)
用不等式可表示为例4.画出下列不等式组表示的平面区域:例5练习:你能用平面区域的方法解下列问题吗?(1)点A(1, 2)与点B(2,-1)在直线x+ay-2=0
的两侧,则a的取值范围是____;(2)已知点A(-2, 3),B(1,2),直线y=kx-2与线段AB有交点,则k的取值范围是____。问题3你能求出由不等式组
表示平面区域的面积吗?小结 ⑴ 二元一次不等式表示平面区域:
直线某一侧所有点组成的平面区域。 ⑵ 判定方法:
直线定界,特殊点定域。 ⑶ 二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分。 知识点 数学思想数形结合、化归、集合、分类讨论
——数轴上的区间。 一元二次不等式的解集——不等式的边界即方程。 思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形? 二、新知探究: (2)探究 特殊:二元一次不等式x – y < 6的解集所表示的图形。 作出x – y = 6的图像——一条直线,
直线把平面分成两部分:左上方区域和右下方区域。 3、探究二元一次不等式(组)的解集表示的图形 左上方区域右下方区域二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 (2)探究 验证:设点P(x,y 1)是直线x – y = 6上的点,选取点A(x,y 2),使它的坐标满足不等式x – y < 6,请完成下面的表格, 二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 结论 在平面直角坐标系中,以二元一次不等式x – y < 6的解为坐标的点都在直线x – y = 6的左上方;反过来,直线x – y = 6左上方的点的坐标都满足不等式x – y < 6。 二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 结论 不等式x – y < 6表示直线x – y = 6左上方的平面区域; 不等式x – y > 6表示直线x – y = 6右下方的平面区域; 直线叫做这两个区域的边界。 二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 从特殊到一般情况: 二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线) 结论一 二元一次不等式表示相应直线的某一侧区域二、新知探究: 4.二元一次不等式表示哪个平面区域的判断方法 直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域,C≠0时,常把原点作为特殊点,C=0时(0,1)(1,0)等。结论二直线定界,特殊点定域。 同侧同号,异侧异号例1:画出不等式 x + 4y < 4表示的平面区域 解:(1)直线定界:先画直线x + 4y – 4 = 0(画成虚线)(2)特殊点定域:取原点(0,0),代入x + 4y - 4,因为 0 + 4×0 – 4 = -4 < 0所以,原点在x + 4y – 4 < 0表示的平面区域内,
不等式x + 4y – 4 < 0表示的区域如图所示。三、例题示范:课堂练习1:(1)画出不等式4x―3y≤12
表示的平面区域(2)画出不等式x≥1
表示的平面区域y < -3x+12
x<2y 的解集。例2、用平面区域表示不等式组解:不等式x-y+5≥0表示
直线x-y+5=0上及右
下方的点的集合,x+y≥0表示直线x+y=0
上及右上方的点的集合,x≤3表示直线x=3上及
左方的点的集合。
x+y=0x-y+5=0x=3所以,不等式所表示的平面区域如图所示35-5x-y+5=0x+y=0x=3变式一:
画出不等式(x+2y+1)(x-y+4)<0
表示的平面区域.变式二:由直线x+y+2=0,x+2y+1=0和
2x+y+1=0围成的三角形(包括边界)
用不等式可表示为例4.画出下列不等式组表示的平面区域:例5练习:你能用平面区域的方法解下列问题吗?(1)点A(1, 2)与点B(2,-1)在直线x+ay-2=0
的两侧,则a的取值范围是____;(2)已知点A(-2, 3),B(1,2),直线y=kx-2与线段AB有交点,则k的取值范围是____。问题3你能求出由不等式组
表示平面区域的面积吗?小结 ⑴ 二元一次不等式表示平面区域:
直线某一侧所有点组成的平面区域。 ⑵ 判定方法:
直线定界,特殊点定域。 ⑶ 二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分。 知识点 数学思想数形结合、化归、集合、分类讨论
