人教新课标A版 必修5 第二章 数列›2.2等差数列的前n项课件(共20张PPT)
文档属性
| 名称 | 人教新课标A版 必修5 第二章 数列›2.2等差数列的前n项课件(共20张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 273.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 09:42:25 | ||
图片预览








文档简介
课件20张PPT。等差数列的前n项和 S = a + a + …… + a
【说明】
3.更一般的情形,an= ,d= 知识巩固1. {an}为等差数列 ?2. a、b、c成等差数列 ?an+1- an=dan+1=an+dan= a1+(n-1) dan= kn + b(k、b为常数)am+(n - m) db为a、c 的等差中项AA2b= a+c4.在等差数列{an}中,由 m+n=p+q am+an=ap+aq ? ? ? ? ?5. 在等差数列{an}中a1+an a2+ an-1 a3+ an-2 …===①前100个自然数的和:1+2+3+…+99+100= ;
②前n个奇数的和:1+3+5+…+(2n-2)+(2n-1)= ;
③前n个偶数的和:2+4+6+…+(2n-2)+2n= .
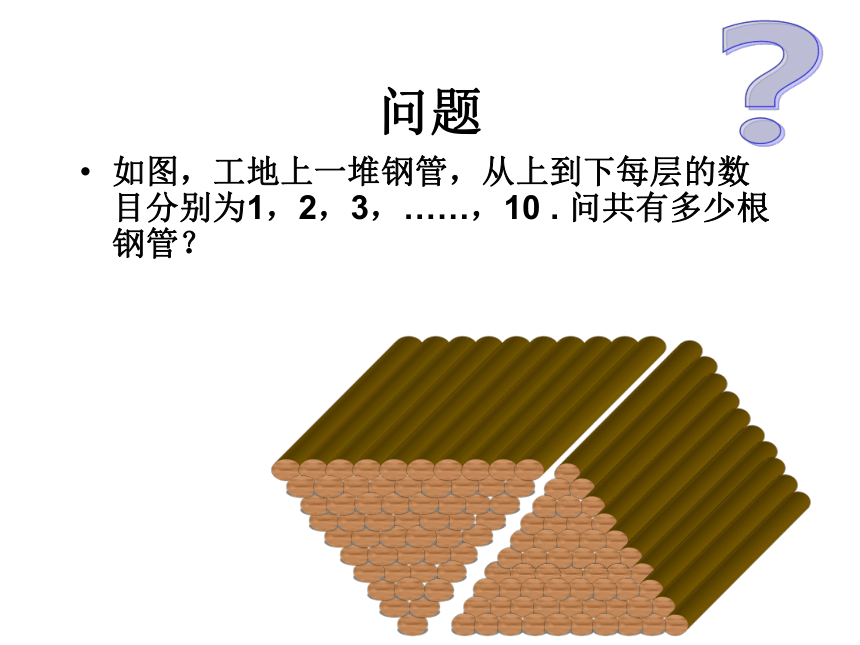
思考:如何求下列和?n2n(n+1)问题如图,工地上一堆钢管,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根钢管??问题如图,工地上一堆钢管,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根钢管??等差数列的前n项和公式的推导由等差数列的前n项和倒
序
相
加 这就是说,等差数列的前n项和等于首末两项的和与项数乘积的一半。公式中代入等差数列的通项公式得到等差数列的前n项和练习11. 根据下列条件,求相应的等差数列 的例1(前n项和公式的应用)解:由题意知,这个V型架自下而上各层的铅笔数成等差数列,记为{an}.答:V型架上共放着7260支铅笔。2如图,一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放1支,最上面一层放120支. 这个V形架上共放了多少支铅笔?对Sn的深入认识an = 4n—14已知一个等差数列an = 4n—14 它是一个关于n的一次函数,它的图象是在一条直线上的若干点。Sn = 2n2-12n它的前n项和是Sn = 2n2-12n 这是一个关于n的二次函数,且二次函数的常数项为0. 反之若一个数列{an},它的前n项和的表达式是关于n的二次函数,且二次函数的常数项为0,则这个数列是等差数列它的图象是抛物线上的若干点。例2.已知数列{an}的前n项和公式为Sn=2n2-30n
(1)这个数列是等差数列吗?求出它的通项公式; (2)求使得Sn最小的序号n的值。解:(1)将n-1代入到数列的前n项和公式,
得Sn-1=2(n-1)2-30(n-1),因此an=Sn-Sn-1=4n-32,(n≥2),当n=1时,a1=S1=2-30=-28,也适合上式,
所以这个数列的通项公式是an=4n-32。例2。前n项和公式的认识,已知前n项和求通项(2)因为 又因为n是正整数,
所以当n=7或=8时,Sn最小,
最小值是-112.小结若为等差数列,则1. 若数列的前n项和为 则数列( )(A)是公差为2的等差数列
(B)是公差为5的等差数列
(C)是公差为10的等差数列
(D)是公差为-10的等差数列C课堂练习:2、已知数列的前n项为 ,
若 ,求3 等差数列-10,-6,-2,2, …
的前多少项的和为54?解:设题中的等差数列是{an},前n项和为Sn.则a1=-10,d=-6-(-10)=4,Sn=54.由等差数列前n项和公式,得解得 n1=9,n2=-3(舍去).因此,等差数列的前9项和是54. 4.已知一个等差数列的前10项的和是310,前20项的和是1220,求其前n项和的公式.解:5.在等差数列{an}中,a2+a4=p,a3+a5=q.则其前 6项的和S6为( )
(A) 5 (p+q)/4 (B) 3(p+q)/2 (C) p+q (D) 2(p+q)B6. 已知等差数列{an}的前n项和为Sn,
若a4=18- a5,则S8等于( )
A.18 B.36 C.54 D.72 D
【说明】
3.更一般的情形,an= ,d= 知识巩固1. {an}为等差数列 ?2. a、b、c成等差数列 ?an+1- an=dan+1=an+dan= a1+(n-1) dan= kn + b(k、b为常数)am+(n - m) db为a、c 的等差中项AA2b= a+c4.在等差数列{an}中,由 m+n=p+q am+an=ap+aq ? ? ? ? ?5. 在等差数列{an}中a1+an a2+ an-1 a3+ an-2 …===①前100个自然数的和:1+2+3+…+99+100= ;
②前n个奇数的和:1+3+5+…+(2n-2)+(2n-1)= ;
③前n个偶数的和:2+4+6+…+(2n-2)+2n= .
思考:如何求下列和?n2n(n+1)问题如图,工地上一堆钢管,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根钢管??问题如图,工地上一堆钢管,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根钢管??等差数列的前n项和公式的推导由等差数列的前n项和倒
序
相
加 这就是说,等差数列的前n项和等于首末两项的和与项数乘积的一半。公式中代入等差数列的通项公式得到等差数列的前n项和练习11. 根据下列条件,求相应的等差数列 的例1(前n项和公式的应用)解:由题意知,这个V型架自下而上各层的铅笔数成等差数列,记为{an}.答:V型架上共放着7260支铅笔。2如图,一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放1支,最上面一层放120支. 这个V形架上共放了多少支铅笔?对Sn的深入认识an = 4n—14已知一个等差数列an = 4n—14 它是一个关于n的一次函数,它的图象是在一条直线上的若干点。Sn = 2n2-12n它的前n项和是Sn = 2n2-12n 这是一个关于n的二次函数,且二次函数的常数项为0. 反之若一个数列{an},它的前n项和的表达式是关于n的二次函数,且二次函数的常数项为0,则这个数列是等差数列它的图象是抛物线上的若干点。例2.已知数列{an}的前n项和公式为Sn=2n2-30n
(1)这个数列是等差数列吗?求出它的通项公式; (2)求使得Sn最小的序号n的值。解:(1)将n-1代入到数列的前n项和公式,
得Sn-1=2(n-1)2-30(n-1),因此an=Sn-Sn-1=4n-32,(n≥2),当n=1时,a1=S1=2-30=-28,也适合上式,
所以这个数列的通项公式是an=4n-32。例2。前n项和公式的认识,已知前n项和求通项(2)因为 又因为n是正整数,
所以当n=7或=8时,Sn最小,
最小值是-112.小结若为等差数列,则1. 若数列的前n项和为 则数列( )(A)是公差为2的等差数列
(B)是公差为5的等差数列
(C)是公差为10的等差数列
(D)是公差为-10的等差数列C课堂练习:2、已知数列的前n项为 ,
若 ,求3 等差数列-10,-6,-2,2, …
的前多少项的和为54?解:设题中的等差数列是{an},前n项和为Sn.则a1=-10,d=-6-(-10)=4,Sn=54.由等差数列前n项和公式,得解得 n1=9,n2=-3(舍去).因此,等差数列的前9项和是54. 4.已知一个等差数列的前10项的和是310,前20项的和是1220,求其前n项和的公式.解:5.在等差数列{an}中,a2+a4=p,a3+a5=q.则其前 6项的和S6为( )
(A) 5 (p+q)/4 (B) 3(p+q)/2 (C) p+q (D) 2(p+q)B6. 已知等差数列{an}的前n项和为Sn,
若a4=18- a5,则S8等于( )
A.18 B.36 C.54 D.72 D
