人教版数学八年级下册 18.1 平行四边形 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册 18.1 平行四边形 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 147.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 14:58:05 | ||
图片预览


文档简介
18.1 平行四边形
一.选择题(共11小题)
1.已知四边形ABCD的对角线相交于O,给出下列4个条件:①AB∥CD②AB=CD③OA=OC④∠BAD=∠BCD;从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有( )
A.4组 B.5组 C.6组 D.3组
2.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB,垂足E在线段AB上,F、G分别是AD、CE的中点,连接FG,EF、CD的延长线交于点H,则下列结论:①;②EF=CF:③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图?ABCD的对角线交于点O,∠ACD=70°,BE⊥AC,则∠ABE的度数为( )
A.50° B.40° C.30° D.20°
4.如图,在平行四边形ABCD中,点E是BC的中点,作EF⊥AE交CD于F,若∠BAE=45°,AE=4,下列结论:①∠EAF=45°,②AF=AB+CF,③CD=2CF,④S△AEF=8中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
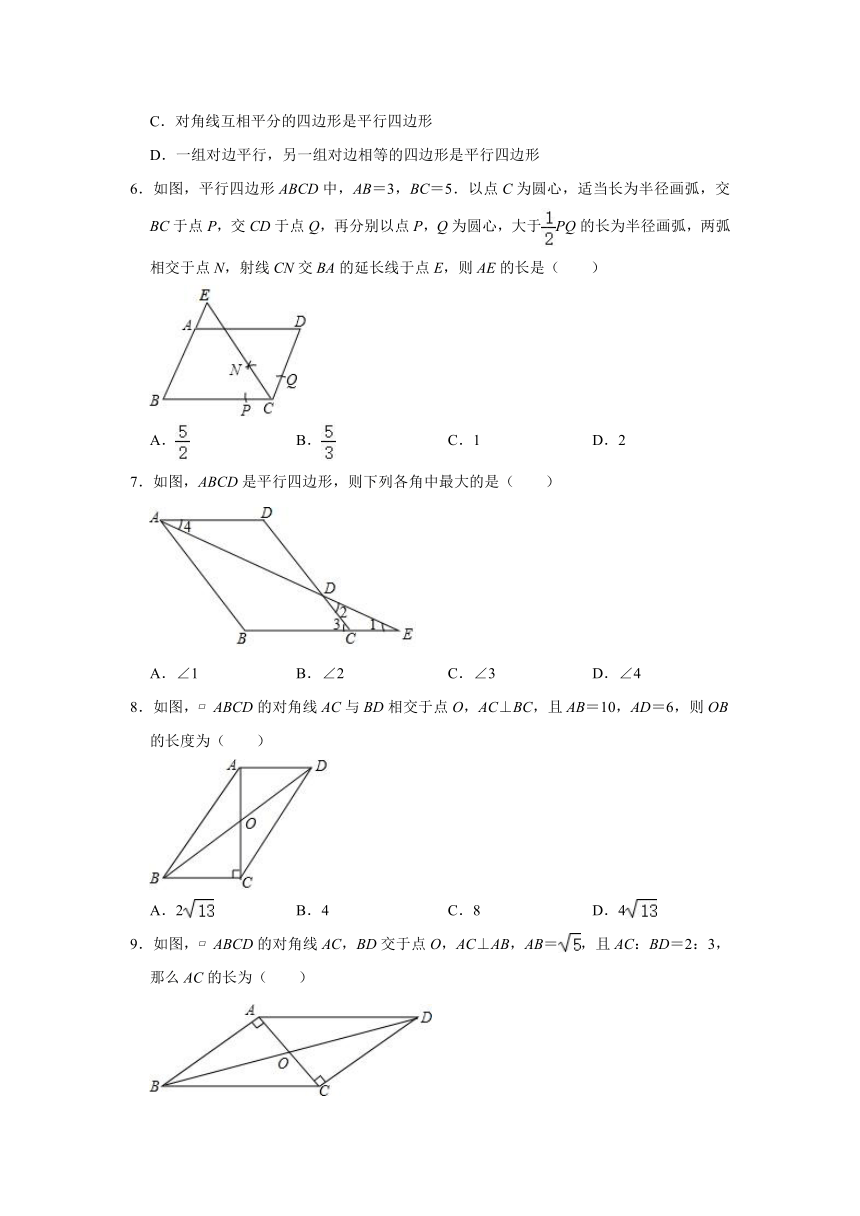
5.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.两组对角分別相等的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
6.如图,平行四边形ABCD中,AB=3,BC=5.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A. B. C.1 D.2
7.如图,ABCD是平行四边形,则下列各角中最大的是( )
A.∠1 B.∠2 C.∠3 D.∠4
8.如图,?ABCD的对角线AC与BD相交于点O,AC⊥BC,且AB=10,AD=6,则OB的长度为( )
A.2 B.4 C.8 D.4
9.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为( )
A.2 B. C.3 D.4
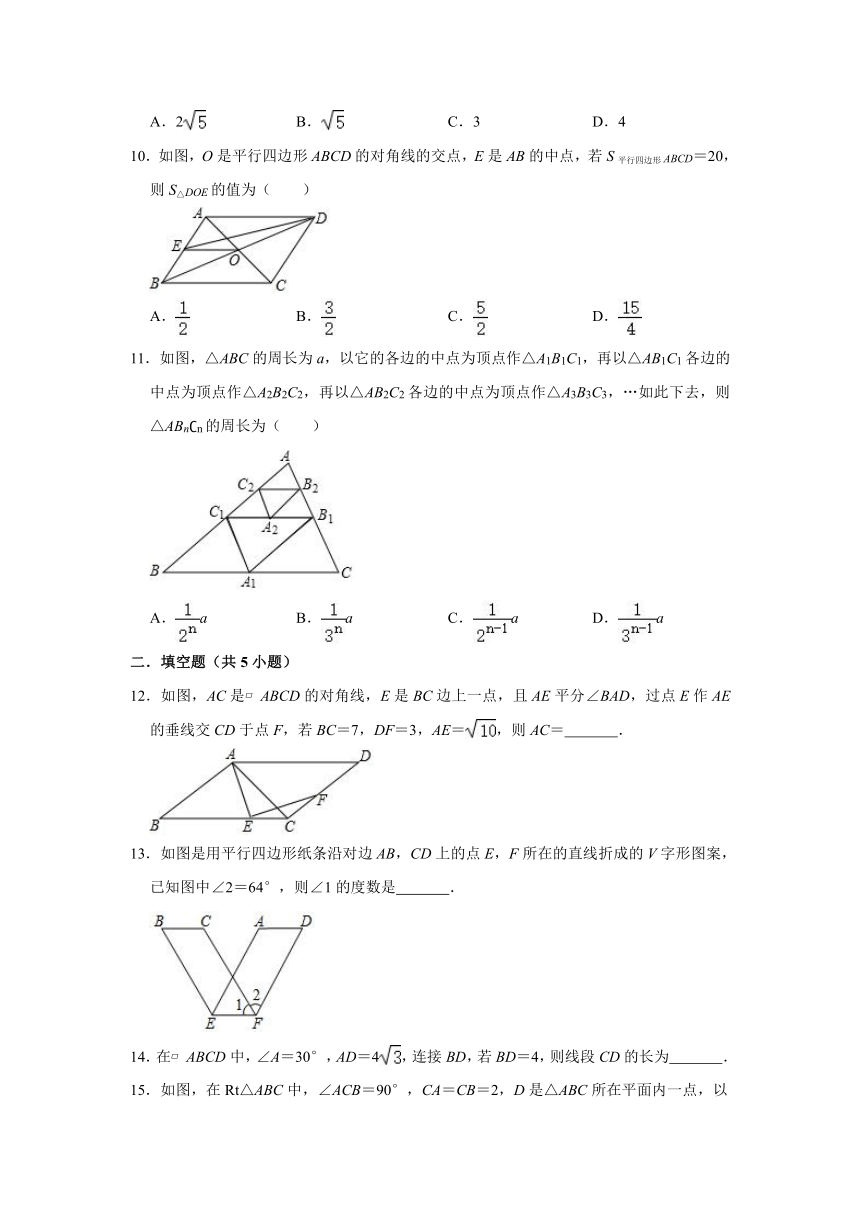
10.如图,O是平行四边形ABCD的对角线的交点,E是AB的中点,若S平行四边形ABCD=20,则S△DOE的值为( )
A. B. C. D.
11.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△ABn?n的周长为( )
A.a B.a C.a D.a
二.填空题(共5小题)
12.如图,AC是?ABCD的对角线,E是BC边上一点,且AE平分∠BAD,过点E作AE的垂线交CD于点F,若BC=7,DF=3,AE=,则AC= .
13.如图是用平行四边形纸条沿对边AB,CD上的点E,F所在的直线折成的V字形图案,已知图中∠2=64°,则∠1的度数是 .
14.在?ABCD中,∠A=30°,AD=4,连接BD,若BD=4,则线段CD的长为 .
15.如图,在Rt△ABC中,∠ACB=90°,CA=CB=2,D是△ABC所在平面内一点,以A,B,C,D为顶点的四边形是平行四边形,则BD的长为 .
16.已知三角形的三条中位线的长分别为5cm、6cm、10cm,则这个三角形的周长是 cm.
三.解答题(共7小题)
17.如图所示平行四边形ABCD中,EF分别是边AD,BC上的点,且AE=CF.
(1)求证:BE=DF;
(2)连结AF,若AD=DF,∠ADF=40°,求∠AFB的度数.
18.已知如图,?ABCD中,∠ABC的平分线BE交AD于点E,∠ADC的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)求证:EF与BD互相平分.
19.如图,在?ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.
(1)若AD=12,AB=8,求CF的长;
(2)连接BE和AF相交于点G,DF和CE相交于点H,求证:EF和GH互相平分.
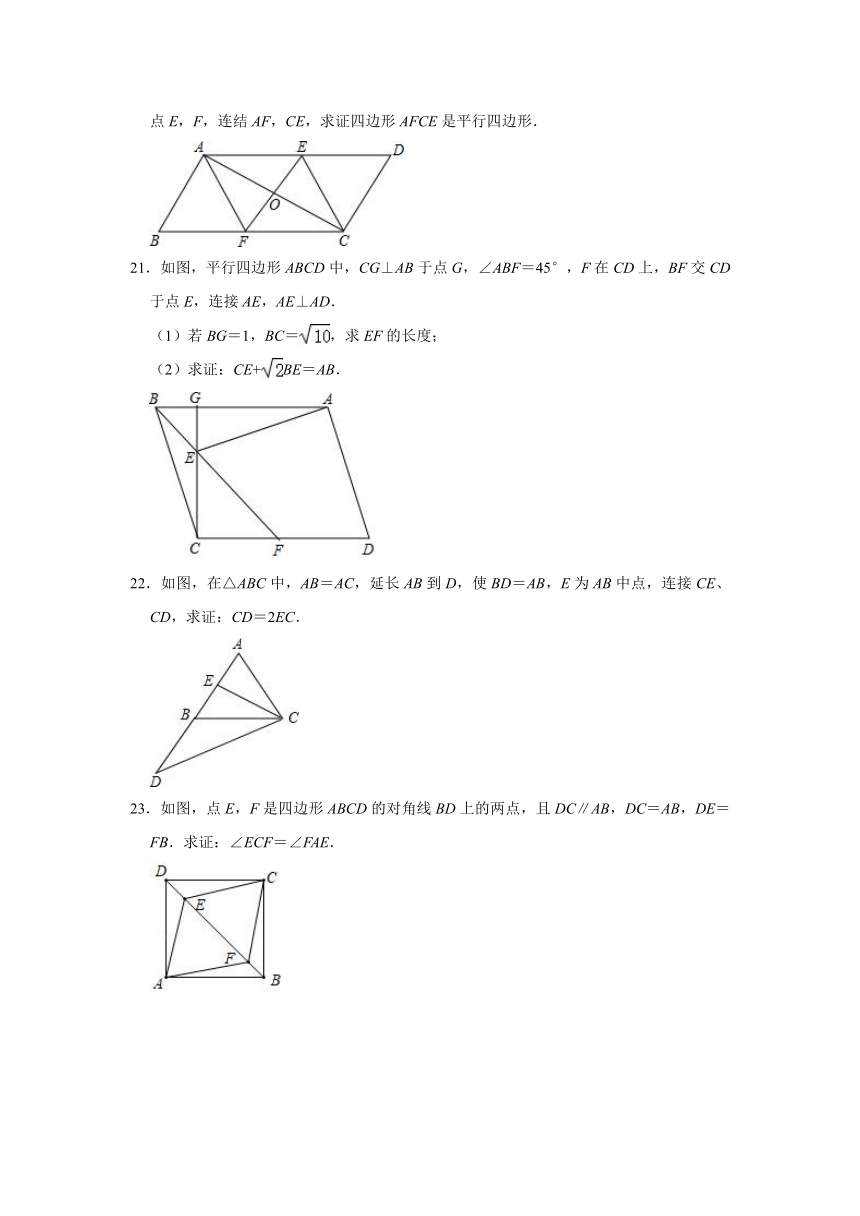
20.如图,在?ABCD中,点O是对角线AC的中点,过点O作直线EF分别交AD、BC于点E,F,连结AF,CE,求证四边形AFCE是平行四边形.
21.如图,平行四边形ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CD于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:CE+BE=AB.
22.如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB中点,连接CE、CD,求证:CD=2EC.
23.如图,点E,F是四边形ABCD的对角线BD上的两点,且DC∥AB,DC=AB,DE=FB.求证:∠ECF=∠FAE.
参考答案
一.选择题(共11小题)
1.
D.
2.
C.
3.
D.
4.
A.
5.
D.
6.
D.
7.
C.
8.
A.
9.
D.
10.
C.
11.
A.
二.填空题(共5小题)
12.
3.
13.
58°.
14.
4或8.
15.
2或2
16.
42.
三.解答题(共7小题)
17.(1)证明:在平行四边形ABCD中,AD∥BC,AD=BC,
∵AE=CF,
∴DE∥BF,DE=BF
∴四边形BEDF是平行四边形
∴BE=DF.
(2)∵AD=DF,∠ADF=40°
∴∠DAF=∠AFD=70°
∵AD∥BC
∴∠AFB=∠FAD=70°.
18.证明:(1)四边形ABCD是平行四边形,
∴AE∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB,
同理:CF=CD,
∴AB=AE=CD=CF,
∵∠A=∠C,
∴△ABE≌△CDF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∴EF与BD互相平分.
19.(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=12,∠BAD=∠BCD,∠ABF=∠CDE,AB=CD,
∴∠DAF=∠AFB,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠AFB=∠BAF,
∴BF=AB=8,
∴CF=BC﹣BF=12﹣8=4;
(2)证明:∵∠BAD=∠BCD,AF平分∠BAD,CE平分∠BCD,
∴∠BAF=∠DAF=∠FCE=∠DCE,
∵∠DAF=∠AFB,
∴∠FCE=∠AFB,
∴AF∥CE,
?ABCD中,AE∥CF,
∴四边形AFCE是平行四边形,
∴AE=CF,
∴DE=BF,
∵AD∥BC,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∵AF∥CE,
∴四边形EGFH是平行四边形,
∴EF和GH互相平分.
20.证明:∵四边形ABD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵点O是对角线AC的中点,
∴OA=OC,
在△AOE和△COF中,,
∴△AOE≌△COF(ASA),
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形.
21.解:(1)∵CG⊥AB,
∴∠AGC=∠CGB=90°,
∵BG=1,BC=,
∴在Rt△BGC中,CG==3,
∵∠ABF=45°,
∴BG=EG=1,
∴CE=2,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GCD=∠BGC=90°,∠EFG=∠GBE=45°,
∴CF=CE=2,
∴EF=CE=2;
(2)如图,延长AE交BC于H,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠AHB=∠HAD,
∵AE⊥AD,
∴∠AHB=∠HAD=90°,
∴∠BAH+∠ABH=∠BCG+∠CBG=90°,
∴∠GAE=∠GCB,
在△BCG与△EAG中,,
∴△BCG≌△EAG(AAS),
∴AG=CG,
∴AB=BG+AG=CE+EG+BG,
∵BG=EG=BE,
∴CE+BE=AB.
22.证明:取AC的中点F,连接BF,
∵AB=AC,点E,F分别是AB,AC的中点,
∴AE=AF,
∵∠A=∠A,AB=AC,
∴△ABF≌△ACE(SAS),
∴BF=CE,
∵BD=AB,AF=CF,
∴DC=2BF,
∴DC=2CE.
23.证明:连接AC交BD于O,如图所示:
∵DC∥AB,DC=AB,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵DE=FB,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∴∠ECF=∠FAE.
一.选择题(共11小题)
1.已知四边形ABCD的对角线相交于O,给出下列4个条件:①AB∥CD②AB=CD③OA=OC④∠BAD=∠BCD;从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有( )
A.4组 B.5组 C.6组 D.3组
2.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB,垂足E在线段AB上,F、G分别是AD、CE的中点,连接FG,EF、CD的延长线交于点H,则下列结论:①;②EF=CF:③S△BEC=2S△CEF;④∠DFE=3∠AEF.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图?ABCD的对角线交于点O,∠ACD=70°,BE⊥AC,则∠ABE的度数为( )
A.50° B.40° C.30° D.20°
4.如图,在平行四边形ABCD中,点E是BC的中点,作EF⊥AE交CD于F,若∠BAE=45°,AE=4,下列结论:①∠EAF=45°,②AF=AB+CF,③CD=2CF,④S△AEF=8中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
5.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.两组对角分別相等的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
6.如图,平行四边形ABCD中,AB=3,BC=5.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A. B. C.1 D.2
7.如图,ABCD是平行四边形,则下列各角中最大的是( )
A.∠1 B.∠2 C.∠3 D.∠4
8.如图,?ABCD的对角线AC与BD相交于点O,AC⊥BC,且AB=10,AD=6,则OB的长度为( )
A.2 B.4 C.8 D.4
9.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为( )
A.2 B. C.3 D.4
10.如图,O是平行四边形ABCD的对角线的交点,E是AB的中点,若S平行四边形ABCD=20,则S△DOE的值为( )
A. B. C. D.
11.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△ABn?n的周长为( )
A.a B.a C.a D.a
二.填空题(共5小题)
12.如图,AC是?ABCD的对角线,E是BC边上一点,且AE平分∠BAD,过点E作AE的垂线交CD于点F,若BC=7,DF=3,AE=,则AC= .
13.如图是用平行四边形纸条沿对边AB,CD上的点E,F所在的直线折成的V字形图案,已知图中∠2=64°,则∠1的度数是 .
14.在?ABCD中,∠A=30°,AD=4,连接BD,若BD=4,则线段CD的长为 .
15.如图,在Rt△ABC中,∠ACB=90°,CA=CB=2,D是△ABC所在平面内一点,以A,B,C,D为顶点的四边形是平行四边形,则BD的长为 .
16.已知三角形的三条中位线的长分别为5cm、6cm、10cm,则这个三角形的周长是 cm.
三.解答题(共7小题)
17.如图所示平行四边形ABCD中,EF分别是边AD,BC上的点,且AE=CF.
(1)求证:BE=DF;
(2)连结AF,若AD=DF,∠ADF=40°,求∠AFB的度数.
18.已知如图,?ABCD中,∠ABC的平分线BE交AD于点E,∠ADC的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)求证:EF与BD互相平分.
19.如图,在?ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.
(1)若AD=12,AB=8,求CF的长;
(2)连接BE和AF相交于点G,DF和CE相交于点H,求证:EF和GH互相平分.
20.如图,在?ABCD中,点O是对角线AC的中点,过点O作直线EF分别交AD、BC于点E,F,连结AF,CE,求证四边形AFCE是平行四边形.
21.如图,平行四边形ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CD于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:CE+BE=AB.
22.如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB中点,连接CE、CD,求证:CD=2EC.
23.如图,点E,F是四边形ABCD的对角线BD上的两点,且DC∥AB,DC=AB,DE=FB.求证:∠ECF=∠FAE.
参考答案
一.选择题(共11小题)
1.
D.
2.
C.
3.
D.
4.
A.
5.
D.
6.
D.
7.
C.
8.
A.
9.
D.
10.
C.
11.
A.
二.填空题(共5小题)
12.
3.
13.
58°.
14.
4或8.
15.
2或2
16.
42.
三.解答题(共7小题)
17.(1)证明:在平行四边形ABCD中,AD∥BC,AD=BC,
∵AE=CF,
∴DE∥BF,DE=BF
∴四边形BEDF是平行四边形
∴BE=DF.
(2)∵AD=DF,∠ADF=40°
∴∠DAF=∠AFD=70°
∵AD∥BC
∴∠AFB=∠FAD=70°.
18.证明:(1)四边形ABCD是平行四边形,
∴AE∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB,
同理:CF=CD,
∴AB=AE=CD=CF,
∵∠A=∠C,
∴△ABE≌△CDF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∴EF与BD互相平分.
19.(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=12,∠BAD=∠BCD,∠ABF=∠CDE,AB=CD,
∴∠DAF=∠AFB,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠AFB=∠BAF,
∴BF=AB=8,
∴CF=BC﹣BF=12﹣8=4;
(2)证明:∵∠BAD=∠BCD,AF平分∠BAD,CE平分∠BCD,
∴∠BAF=∠DAF=∠FCE=∠DCE,
∵∠DAF=∠AFB,
∴∠FCE=∠AFB,
∴AF∥CE,
?ABCD中,AE∥CF,
∴四边形AFCE是平行四边形,
∴AE=CF,
∴DE=BF,
∵AD∥BC,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∵AF∥CE,
∴四边形EGFH是平行四边形,
∴EF和GH互相平分.
20.证明:∵四边形ABD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵点O是对角线AC的中点,
∴OA=OC,
在△AOE和△COF中,,
∴△AOE≌△COF(ASA),
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形.
21.解:(1)∵CG⊥AB,
∴∠AGC=∠CGB=90°,
∵BG=1,BC=,
∴在Rt△BGC中,CG==3,
∵∠ABF=45°,
∴BG=EG=1,
∴CE=2,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GCD=∠BGC=90°,∠EFG=∠GBE=45°,
∴CF=CE=2,
∴EF=CE=2;
(2)如图,延长AE交BC于H,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠AHB=∠HAD,
∵AE⊥AD,
∴∠AHB=∠HAD=90°,
∴∠BAH+∠ABH=∠BCG+∠CBG=90°,
∴∠GAE=∠GCB,
在△BCG与△EAG中,,
∴△BCG≌△EAG(AAS),
∴AG=CG,
∴AB=BG+AG=CE+EG+BG,
∵BG=EG=BE,
∴CE+BE=AB.
22.证明:取AC的中点F,连接BF,
∵AB=AC,点E,F分别是AB,AC的中点,
∴AE=AF,
∵∠A=∠A,AB=AC,
∴△ABF≌△ACE(SAS),
∴BF=CE,
∵BD=AB,AF=CF,
∴DC=2BF,
∴DC=2CE.
23.证明:连接AC交BD于O,如图所示:
∵DC∥AB,DC=AB,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵DE=FB,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∴∠ECF=∠FAE.
