二年级美术上册课件 大树的故事 3(人美版)
文档属性
| 名称 | 二年级美术上册课件 大树的故事 3(人美版) |  | |
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 美术 | ||
| 更新时间 | 2009-12-24 11:44:00 | ||
图片预览


文档简介
同升湖实验学校09-10学年高二上学期第一次月考
数学试卷时量:120分钟,满分:150分 第I卷参考公式:线性回归方程的系数公式为,.一.选择题:本大题共8题,每小题5分,共40分。请把正确答案的代号填在第II卷的选择题答案表中。1、下列给出的赋值语句中正确的是: ( )A、3=A B、M= —M C、B=A=2 D、x+y=02、一个年级有12个班,每个班的同学从1至50排学号,为了交流学习经验,要求每班学号为14的同学留下进行交流,这里运用的是 ( )A.系统抽样 B.分层抽样 C. 抽签抽样 D.随机抽样 3、一个工厂有若干个车间,今采取分层抽样方法从全厂某天的2048件产品中抽取一个容量为128的样本进行质量检查,若某车间这一天生产256件产品,则从该车间抽取的产品件数为( )A.12 B.32 C.8 D. 16 ( 第4题图)4、100辆汽车通过某一段公路时的时速的频率分布直方图如右上图所示,则时速在[60,70)的汽车大约有( )A、30辆 B、40辆 C、60辆 D、80辆 5、已知变量x,y具有线性相关关系,且(x,y)的一组数据为(1,3),(2,3.8),(3,5.2),(4,6),则回归方程是 A.=x+1.9 B.=0.95x+1.04 C.=1.04x+1.9 D.=1.05x-0.96、运行如右程序: 当输入168,72时,输出的结果是 A.72 B. 36 C.24 D. 127、考虑一元二次方程x2+mx+n=0,其中m、n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )A. B. C. D.8.某流 ( http: / / www.21cnjy.com / )程如右图所示,现输入如下四个函数,则可以输出的函数是( )A. B.C. D.二、填空题:本大题共有7小题,每小题5分,满分35分。请把正确答案填在第II卷的填空题答案表中。9、将二进制数101101(2) 化为十进制结果为 _ ;再将该数化为八进制数,结果为 ______.10、甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如表所示:
甲 乙 丙 丁
8.5 8.8 8.8 8
3.5 3.5 2.1 8.7
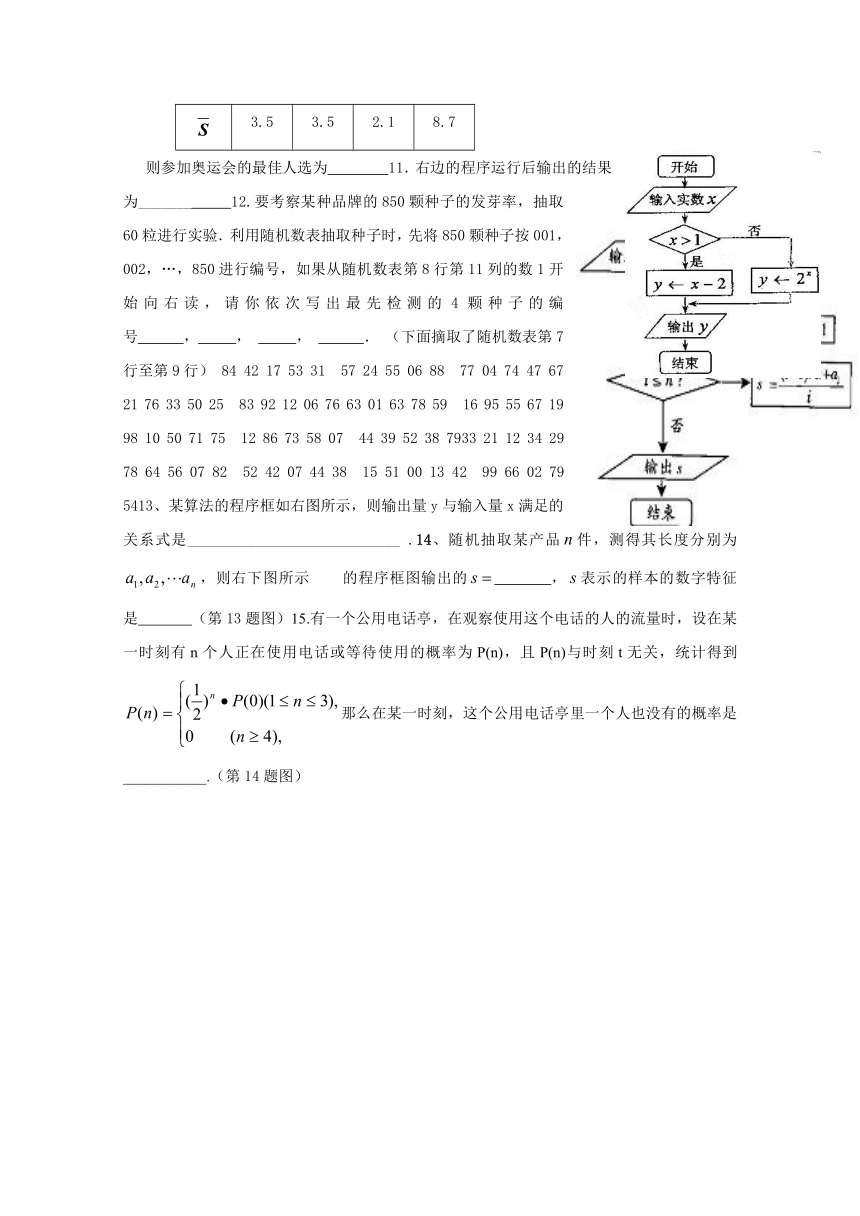
则参加奥运会的最佳人选为 11.右边的程序运行后输出的结果为_______ 12.要考察某种品牌的850颗种子的发芽率,抽取60粒进行实验.利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第8行第11列的数1开始向右读,请你依次写出最先检测的4颗种子的编号 , , , . (下面摘取了随机数表第7行至第9行) 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 5413、某算法的程序框如右图所示,则输出量y与输入量x满足的关系式是____________________________ .14、随机抽取某产品件,测得其长度分别为,则右下图所示 的程序框图输出的 ,表示的样本的数字特征 是 (第13题图)15.有一个公用电话亭,在观察使用这个电话的人的流量时,设在某一时刻有n个人正在使用电话或等待使用的概率为P(n),且P(n)与时刻t无关,统计得到那么在某一时刻,这个公用电话亭里一个人也没有的概率是___________.(第14题图)
第II卷一、选择题答案表:本大题共8题,每小题5分,共40分
题号 1 2 3 4 5 6 7 8
答案
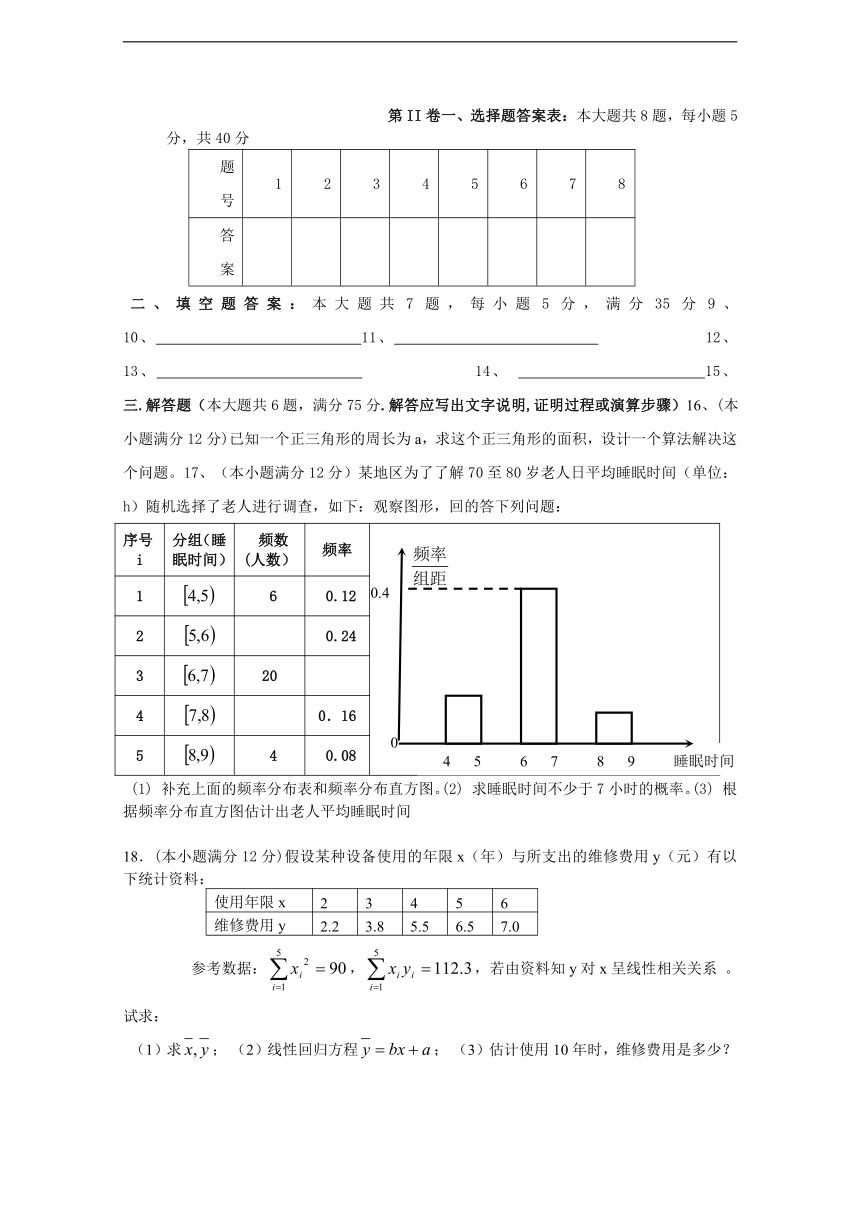
二、填空题答案:本大题共7题,每小题5分,满分35分9、 10、 11、 12、 13、 14、 15、 三.解答题(本大题共6题,满分75分.解答应写出文字说明,证明过程或演算步骤)16、(本小题满分12分)已知一个正三角形的周长为a,求这个正三角形的面积,设计一个算法解决这个问题。17、(本小题满分12分)某地区为了了解70至80岁老人日平均睡眠时间(单位:h)随机选择了老人进行调查,如下:观察图形,回的答下列问题:
序号i 分组(睡眠时间) 频数(人数) 频率
1 6 0.12
2 0.24
3 20
4 0.16
5 4 0.08
(1) 补充上面的频率分布表和频率分布直方图。(2) 求睡眠时间不少于7小时的概率。(3) 根据频率分布直方图估计出老人平均睡眠时间
18.(本小题满分12分)假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x 2 3 4 5 6
维修费用y 2.2 3.8 5.5 6.5 7.0
参考数据:,,若由资料知y对x呈线性相关关系 。试求:
(1)求; (2)线性回归方程; (3)估计使用10年时,维修费用是多少?
19、(本小题满分13分)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图2.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本平均数和方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同
学,求身高为176cm的同学被抽中的概率.
20.(本小题满分13分)一个停车场有5个车位,任意停放“红旗”、“奔驰”、“丰田”、“宝马”、“奥迪”轿车各1辆,试求下列事件的概率:
(1)“红旗”轿车停在边上
(2)“红旗”轿车和“丰田”轿车都停在边上
(3)“红旗”轿车或“丰田”轿车停在边上
21、 (本小题满分13分) 给出30个数:1,2,4,7,…… ,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如右下图所示):
(1)该算法使用什么类型的循环结构;(2)图中 ① 处和 ② 处应填上什么语句,使之能完成该题算法功能,并简单说明你的理由。(3)根据程序框图写出程序.
参考答案
一、选择题答案(本大题共8题,每小题5分,共40分)
题号 1 2 3 4 5 6 7 8
答案 B A D B C C A D
二、填空题答案:(本大题共有3小题,每小题5分,满分35分)
9、 45,55(8) 10、丙 11、3 12、169,555,671,105
13、 14、 平均值
15、
三.解答题:
16、解:算法步骤如下:
S1 输入a的值
S2 计算=.
S3 计算S=,
S4 输出S。
序号i 分组(睡眠时间) 频数(人数) 频率
1 6 0.12
2 12 0.24
3 20 0.4
4 8 0.16
5 4 0.08
17、
(1)
(2)由(1)可知睡眠时间不少于7小时的概率为 0.16+0.08=0.24
所以睡眠时间不少于7小时的概率为24%。
(3)平均睡眠时间4.50.12+5.50.24+6.50.4+7.50.16+8.50.08=6.34根据频率分布直方图估计出老人平均睡眠时间6.34h
18、解:(1)(2)由已知可得:
于是 所以,回归直线方程是:。
(3)由第(2)可得,当时,(万元)
即估计使用10年时,维修费用是12.38万元。
19、解:(1)由茎叶图可知:甲班身高集中于之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
(2)
甲班的样本方差为
=57
(3)设“身高为176cm的同学被抽中”的事件为A.
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173),(181,176), (181,178),(181,179),(179,173),(179,176),(179,178),(178,173), (178, 176),(176,173)共10个基本事件,而事件A含有4个基本事件,
20.解:由题意可知,基本事件总数为:5×4×3×2×1=120
记“‘红旗’轿车停在边上”为事件A,
事件A包含的基本事件数为:4×3×2×1+4×3×2×1=48
所以P(A)==
21.解:(1)该算法使用了当型循环结构. (2) ① 处应填;②处应填;
因为是求30个数的和,故循环体应执行30次,其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为.算法 中的变量p实质是表示参与求和的各个数,由于它也是变化的,且满足第i个数比其前一个数大,,第个数比其前一个数大i,故应有;
(3)程序如右图所示
www.
时速(km)
0.01
0.02
0.03
0.04
频率
组距
40
50
60
70
80
INPUT m , n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
EN D
第6题图
(第11题)
否
存在零点?
输出函数
结束
是
开始
输入函数
是
否
(第8题)图
x=5
y=-12
IF x<0 Then
x=y-3
Else
x=y+3
End If
Print x-y
End (第11题)
4 5 6 7 8 9 睡眠时间按
0
0.4
②
①
N
Y
4 5 6 7 8 9 体重
0
0.4
i=1
p=1
s=0
WHILE i<=30
s=s+p
p=p+i
i=i+1
WEND
PRINT s
END
数学试卷时量:120分钟,满分:150分 第I卷参考公式:线性回归方程的系数公式为,.一.选择题:本大题共8题,每小题5分,共40分。请把正确答案的代号填在第II卷的选择题答案表中。1、下列给出的赋值语句中正确的是: ( )A、3=A B、M= —M C、B=A=2 D、x+y=02、一个年级有12个班,每个班的同学从1至50排学号,为了交流学习经验,要求每班学号为14的同学留下进行交流,这里运用的是 ( )A.系统抽样 B.分层抽样 C. 抽签抽样 D.随机抽样 3、一个工厂有若干个车间,今采取分层抽样方法从全厂某天的2048件产品中抽取一个容量为128的样本进行质量检查,若某车间这一天生产256件产品,则从该车间抽取的产品件数为( )A.12 B.32 C.8 D. 16 ( 第4题图)4、100辆汽车通过某一段公路时的时速的频率分布直方图如右上图所示,则时速在[60,70)的汽车大约有( )A、30辆 B、40辆 C、60辆 D、80辆 5、已知变量x,y具有线性相关关系,且(x,y)的一组数据为(1,3),(2,3.8),(3,5.2),(4,6),则回归方程是 A.=x+1.9 B.=0.95x+1.04 C.=1.04x+1.9 D.=1.05x-0.96、运行如右程序: 当输入168,72时,输出的结果是 A.72 B. 36 C.24 D. 127、考虑一元二次方程x2+mx+n=0,其中m、n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )A. B. C. D.8.某流 ( http: / / www.21cnjy.com / )程如右图所示,现输入如下四个函数,则可以输出的函数是( )A. B.C. D.二、填空题:本大题共有7小题,每小题5分,满分35分。请把正确答案填在第II卷的填空题答案表中。9、将二进制数101101(2) 化为十进制结果为 _ ;再将该数化为八进制数,结果为 ______.10、甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如表所示:
甲 乙 丙 丁
8.5 8.8 8.8 8
3.5 3.5 2.1 8.7
则参加奥运会的最佳人选为 11.右边的程序运行后输出的结果为_______ 12.要考察某种品牌的850颗种子的发芽率,抽取60粒进行实验.利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第8行第11列的数1开始向右读,请你依次写出最先检测的4颗种子的编号 , , , . (下面摘取了随机数表第7行至第9行) 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 5413、某算法的程序框如右图所示,则输出量y与输入量x满足的关系式是____________________________ .14、随机抽取某产品件,测得其长度分别为,则右下图所示 的程序框图输出的 ,表示的样本的数字特征 是 (第13题图)15.有一个公用电话亭,在观察使用这个电话的人的流量时,设在某一时刻有n个人正在使用电话或等待使用的概率为P(n),且P(n)与时刻t无关,统计得到那么在某一时刻,这个公用电话亭里一个人也没有的概率是___________.(第14题图)
第II卷一、选择题答案表:本大题共8题,每小题5分,共40分
题号 1 2 3 4 5 6 7 8
答案
二、填空题答案:本大题共7题,每小题5分,满分35分9、 10、 11、 12、 13、 14、 15、 三.解答题(本大题共6题,满分75分.解答应写出文字说明,证明过程或演算步骤)16、(本小题满分12分)已知一个正三角形的周长为a,求这个正三角形的面积,设计一个算法解决这个问题。17、(本小题满分12分)某地区为了了解70至80岁老人日平均睡眠时间(单位:h)随机选择了老人进行调查,如下:观察图形,回的答下列问题:
序号i 分组(睡眠时间) 频数(人数) 频率
1 6 0.12
2 0.24
3 20
4 0.16
5 4 0.08
(1) 补充上面的频率分布表和频率分布直方图。(2) 求睡眠时间不少于7小时的概率。(3) 根据频率分布直方图估计出老人平均睡眠时间
18.(本小题满分12分)假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x 2 3 4 5 6
维修费用y 2.2 3.8 5.5 6.5 7.0
参考数据:,,若由资料知y对x呈线性相关关系 。试求:
(1)求; (2)线性回归方程; (3)估计使用10年时,维修费用是多少?
19、(本小题满分13分)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图2.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本平均数和方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同
学,求身高为176cm的同学被抽中的概率.
20.(本小题满分13分)一个停车场有5个车位,任意停放“红旗”、“奔驰”、“丰田”、“宝马”、“奥迪”轿车各1辆,试求下列事件的概率:
(1)“红旗”轿车停在边上
(2)“红旗”轿车和“丰田”轿车都停在边上
(3)“红旗”轿车或“丰田”轿车停在边上
21、 (本小题满分13分) 给出30个数:1,2,4,7,…… ,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如右下图所示):
(1)该算法使用什么类型的循环结构;(2)图中 ① 处和 ② 处应填上什么语句,使之能完成该题算法功能,并简单说明你的理由。(3)根据程序框图写出程序.
参考答案
一、选择题答案(本大题共8题,每小题5分,共40分)
题号 1 2 3 4 5 6 7 8
答案 B A D B C C A D
二、填空题答案:(本大题共有3小题,每小题5分,满分35分)
9、 45,55(8) 10、丙 11、3 12、169,555,671,105
13、 14、 平均值
15、
三.解答题:
16、解:算法步骤如下:
S1 输入a的值
S2 计算=.
S3 计算S=,
S4 输出S。
序号i 分组(睡眠时间) 频数(人数) 频率
1 6 0.12
2 12 0.24
3 20 0.4
4 8 0.16
5 4 0.08
17、
(1)
(2)由(1)可知睡眠时间不少于7小时的概率为 0.16+0.08=0.24
所以睡眠时间不少于7小时的概率为24%。
(3)平均睡眠时间4.50.12+5.50.24+6.50.4+7.50.16+8.50.08=6.34根据频率分布直方图估计出老人平均睡眠时间6.34h
18、解:(1)(2)由已知可得:
于是 所以,回归直线方程是:。
(3)由第(2)可得,当时,(万元)
即估计使用10年时,维修费用是12.38万元。
19、解:(1)由茎叶图可知:甲班身高集中于之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
(2)
甲班的样本方差为
=57
(3)设“身高为176cm的同学被抽中”的事件为A.
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173),(181,176), (181,178),(181,179),(179,173),(179,176),(179,178),(178,173), (178, 176),(176,173)共10个基本事件,而事件A含有4个基本事件,
20.解:由题意可知,基本事件总数为:5×4×3×2×1=120
记“‘红旗’轿车停在边上”为事件A,
事件A包含的基本事件数为:4×3×2×1+4×3×2×1=48
所以P(A)==
21.解:(1)该算法使用了当型循环结构. (2) ① 处应填;②处应填;
因为是求30个数的和,故循环体应执行30次,其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为.算法 中的变量p实质是表示参与求和的各个数,由于它也是变化的,且满足第i个数比其前一个数大,,第个数比其前一个数大i,故应有;
(3)程序如右图所示
www.
时速(km)
0.01
0.02
0.03
0.04
频率
组距
40
50
60
70
80
INPUT m , n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
EN D
第6题图
(第11题)
否
存在零点?
输出函数
结束
是
开始
输入函数
是
否
(第8题)图
x=5
y=-12
IF x<0 Then
x=y-3
Else
x=y+3
End If
Print x-y
End (第11题)
4 5 6 7 8 9 睡眠时间按
0
0.4
②
①
N
Y
4 5 6 7 8 9 体重
0
0.4
i=1
p=1
s=0
WHILE i<=30
s=s+p
p=p+i
i=i+1
WEND
PRINT s
END
同课章节目录
