2020鲁教版五四制七上数学1.3探索三角形全等的条件第1课时课件(27张)
文档属性
| 名称 | 2020鲁教版五四制七上数学1.3探索三角形全等的条件第1课时课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-19 22:36:34 | ||
图片预览





文档简介
课件27张PPT。3 探索三角形全等的条件
第1课时1.会用“边边边”判定三角形全等.
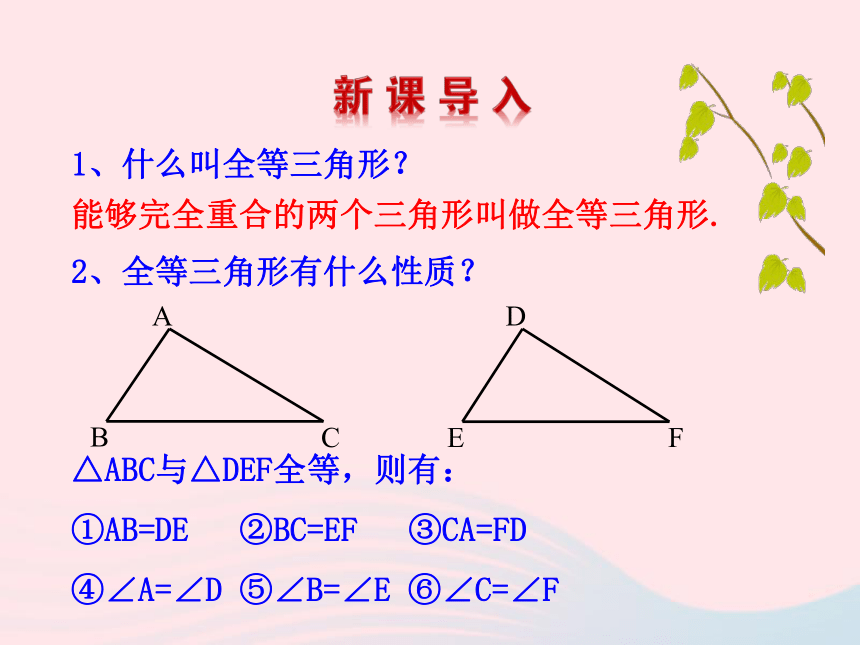
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.△ABC与△DEF全等,则有:
①AB=DE ②BC=EF ③CA=FD
④∠A=∠D ⑤∠B=∠E ⑥∠C=∠F1、什么叫全等三角形?能够完全重合的两个三角形叫做全等三角形.2、全等三角形有什么性质?问题一:
根据上面的结论,两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形中上述六个元素对应相等,是否一定全等?问题二:
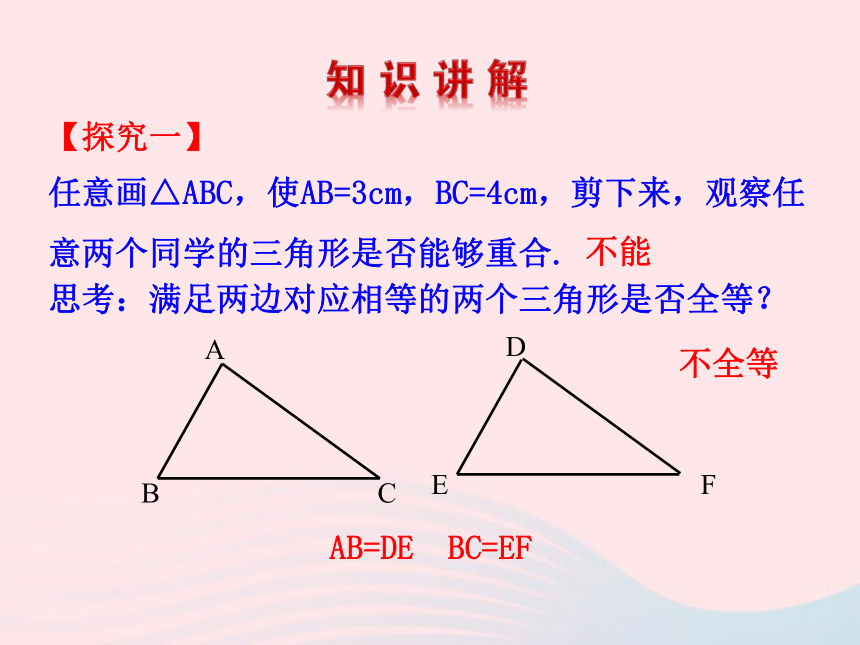
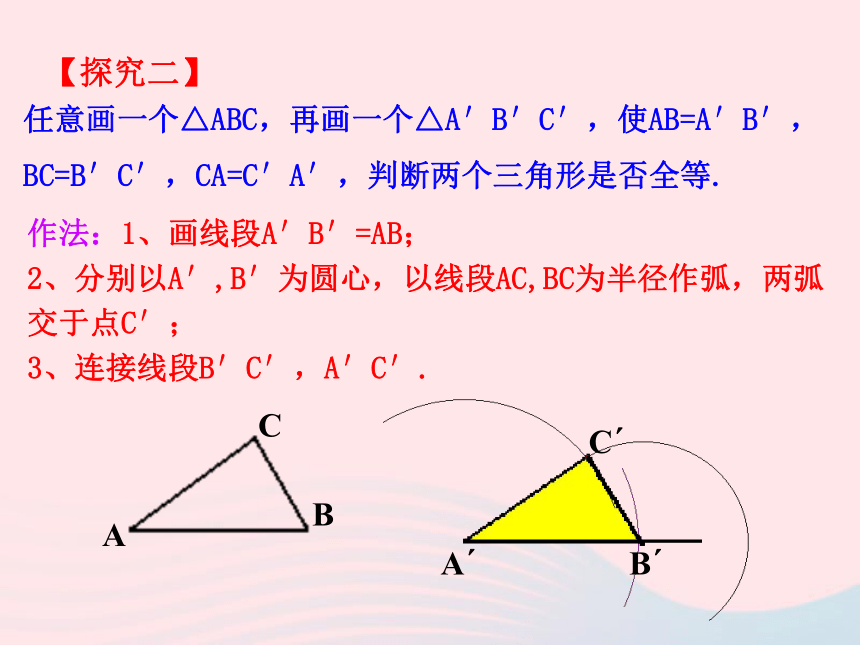
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否也能说明它们全等?任意画△ABC,使AB=3cm,BC=4cm,剪下来,观察任意两个同学的三角形是否能够重合.AB=DE BC=EF思考:满足两边对应相等的两个三角形是否全等?不能不全等【探究一】任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等.作法:1、画线段A′B′=AB;
2、分别以A′,B′为圆心,以线段AC,BC为半径作弧,两弧交于点C′;
3、连接线段B′C′,A′C′.A′B′C′【探究二】剪下 △A′B′C′放在△ABC上,可以看到△A′B′C′ ≌ △ABC,由此可以得到判定两个三角形全等的一个定理.用数学语言表述:在△ABC和△DEF中所以 △ABC ≌△DEF(SSS)三角形全等判定定理一:
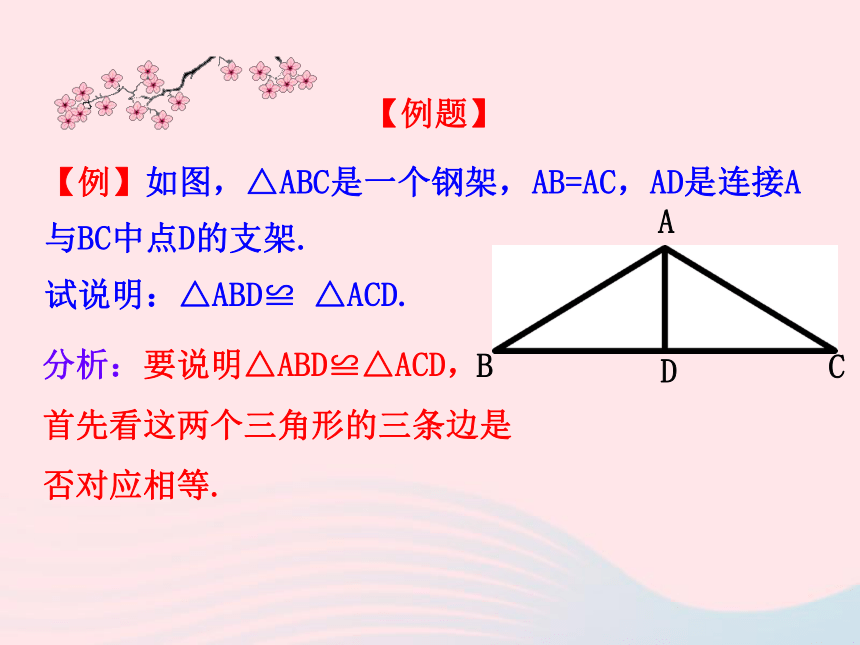
三边分别相等的两个三角形全等 , 简写为“边边边”或“SSS”.因为【例】如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架.
试说明:△ABD≌ △ACD.分析:要说明△ABD≌△ACD,
首先看这两个三角形的三条边是
否对应相等.【例题】解析:因为 D是BC的中点
所以 BD=CD在△ABD和△ACD中,AB=AC (已知)BD=CD (已证)AD=AD (公共边)所以 △ABD ≌ △ACD (SSS)因为(1)准备条件:说明全等时要用的间接条件要先准备好;(2)三角形全等书写三步骤:①写出在哪两个三角形中;②摆出三个条件用大括号括起来;③写出全等结论.说明理由的书写步骤:【归纳】解析:△ABC≌△DCB
理由如下:
AB = DC,
AC = DB,
BC= CB,△ABC≌ △DCB(SSS), 2.如图,D,F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件 . 1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?BF=CD或BD=CF【跟踪训练】 所以 △ABD ≌△CDB3.如图,在四边形ABCD中AB=CD,AD=BC,则∠A=∠C.请说明理由.解析:在△ABD和△CDB中AB=CD (已知)AD=CB (已知)BD=DB(公共边)(SSS)所以 ∠A= ∠C( )全等三角形的对应角相等 利用前面的结论,你可以得到作一个角等于已知角的方法吗?【问题】已知:∠AOB,求作:∠A′O′B′=∠AOB.OABCDO′A′B′C′D′作法:1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB.三角形的稳定性三角形具有稳定性,
四边形不具有稳定性. 盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?【探究交流】三角形的稳定性 将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?不会,三角形具有稳定性.【生活体验】斜梁斜梁横 梁三角形的稳定性【生活体验】如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法依据的是三角形的稳定性.三角形的稳定性【生活体验】四边形不稳定性的应用活动挂衣架【生活体验】1.下列图形中具有稳定性的是( )(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形C2.要使下列木架稳定各至少需要多少根木棍?一根 两根 三根【学以致用】1.如图,AB=AC,AE=AD,BD=CE,
试说明:△AEB ≌ △ ADC.【解析】 因为BD=CE,所以 BD-ED=CE-ED,所以BE=CD.CABDE在△ AEB和△ ADC中,
AB=AC,
AE=AD,
BE=CD,
所以△AEB ≌△ADC(SSS)2.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”说明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?【解析】要说明△ABC ≌△FDE,还应该有AB=FD这个条件.因为DB是AB与DF的公共部分,且AD=BF,
所以AD+DB=BF+DB,即AB=FD.3.(昆明·中考)如图,点B,D,C,F在一条直线上,且BC=FD,AB=EF.
(1)请你只添加一个条件(不再加辅助线),
使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,试说明△ABC≌△EFD.【解析】 (1) AC=ED.(2)在△ ABC和△ EFD中,
AB=EF,
BC=FD,
AC=ED,
所以△ABC≌△EFD(SSS). 通过本课时的学习,需要我们掌握:1.三角形全等的判定定理一——SSS.
2.利用SSS解决简单的三角形全等问题. 在数学这门科学里,我们发现真理的主要工具是归纳和类比.
——拉普拉斯
第1课时1.会用“边边边”判定三角形全等.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.△ABC与△DEF全等,则有:
①AB=DE ②BC=EF ③CA=FD
④∠A=∠D ⑤∠B=∠E ⑥∠C=∠F1、什么叫全等三角形?能够完全重合的两个三角形叫做全等三角形.2、全等三角形有什么性质?问题一:
根据上面的结论,两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形中上述六个元素对应相等,是否一定全等?问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否也能说明它们全等?任意画△ABC,使AB=3cm,BC=4cm,剪下来,观察任意两个同学的三角形是否能够重合.AB=DE BC=EF思考:满足两边对应相等的两个三角形是否全等?不能不全等【探究一】任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等.作法:1、画线段A′B′=AB;
2、分别以A′,B′为圆心,以线段AC,BC为半径作弧,两弧交于点C′;
3、连接线段B′C′,A′C′.A′B′C′【探究二】剪下 △A′B′C′放在△ABC上,可以看到△A′B′C′ ≌ △ABC,由此可以得到判定两个三角形全等的一个定理.用数学语言表述:在△ABC和△DEF中所以 △ABC ≌△DEF(SSS)三角形全等判定定理一:
三边分别相等的两个三角形全等 , 简写为“边边边”或“SSS”.因为【例】如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架.
试说明:△ABD≌ △ACD.分析:要说明△ABD≌△ACD,
首先看这两个三角形的三条边是
否对应相等.【例题】解析:因为 D是BC的中点
所以 BD=CD在△ABD和△ACD中,AB=AC (已知)BD=CD (已证)AD=AD (公共边)所以 △ABD ≌ △ACD (SSS)因为(1)准备条件:说明全等时要用的间接条件要先准备好;(2)三角形全等书写三步骤:①写出在哪两个三角形中;②摆出三个条件用大括号括起来;③写出全等结论.说明理由的书写步骤:【归纳】解析:△ABC≌△DCB
理由如下:
AB = DC,
AC = DB,
BC= CB,△ABC≌ △DCB(SSS), 2.如图,D,F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件 . 1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?BF=CD或BD=CF【跟踪训练】 所以 △ABD ≌△CDB3.如图,在四边形ABCD中AB=CD,AD=BC,则∠A=∠C.请说明理由.解析:在△ABD和△CDB中AB=CD (已知)AD=CB (已知)BD=DB(公共边)(SSS)所以 ∠A= ∠C( )全等三角形的对应角相等 利用前面的结论,你可以得到作一个角等于已知角的方法吗?【问题】已知:∠AOB,求作:∠A′O′B′=∠AOB.OABCDO′A′B′C′D′作法:1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB.三角形的稳定性三角形具有稳定性,
四边形不具有稳定性. 盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?【探究交流】三角形的稳定性 将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?不会,三角形具有稳定性.【生活体验】斜梁斜梁横 梁三角形的稳定性【生活体验】如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法依据的是三角形的稳定性.三角形的稳定性【生活体验】四边形不稳定性的应用活动挂衣架【生活体验】1.下列图形中具有稳定性的是( )(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形C2.要使下列木架稳定各至少需要多少根木棍?一根 两根 三根【学以致用】1.如图,AB=AC,AE=AD,BD=CE,
试说明:△AEB ≌ △ ADC.【解析】 因为BD=CE,所以 BD-ED=CE-ED,所以BE=CD.CABDE在△ AEB和△ ADC中,
AB=AC,
AE=AD,
BE=CD,
所以△AEB ≌△ADC(SSS)2.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”说明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?【解析】要说明△ABC ≌△FDE,还应该有AB=FD这个条件.因为DB是AB与DF的公共部分,且AD=BF,
所以AD+DB=BF+DB,即AB=FD.3.(昆明·中考)如图,点B,D,C,F在一条直线上,且BC=FD,AB=EF.
(1)请你只添加一个条件(不再加辅助线),
使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,试说明△ABC≌△EFD.【解析】 (1) AC=ED.(2)在△ ABC和△ EFD中,
AB=EF,
BC=FD,
AC=ED,
所以△ABC≌△EFD(SSS). 通过本课时的学习,需要我们掌握:1.三角形全等的判定定理一——SSS.
2.利用SSS解决简单的三角形全等问题. 在数学这门科学里,我们发现真理的主要工具是归纳和类比.
——拉普拉斯
