人教版高中数学2019-2020 必修三 第二章 2.2.2 方差和标准差(网课)(共15张PPT)
文档属性
| 名称 | 人教版高中数学2019-2020 必修三 第二章 2.2.2 方差和标准差(网课)(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 918.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
方差和标准差
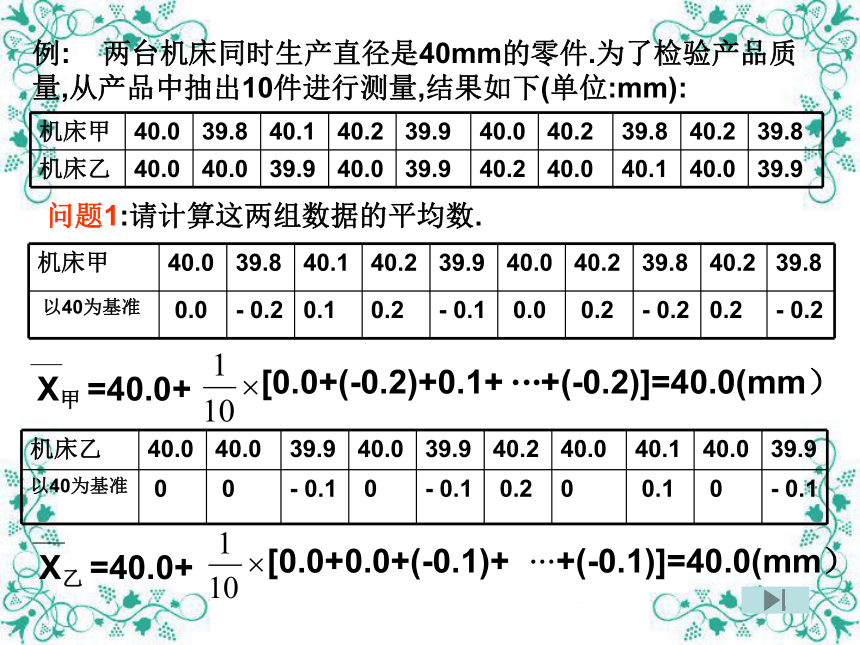
例: 两台机床同时生产直径是40mm的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:mm):
问题1:请计算这两组数据的平均数.
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
以40为基准 0.0 - 0.2 0.1 0.2 - 0.1 0.0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
以40为基准 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
例: 两台机床同时生产直径是40mm的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:mm):
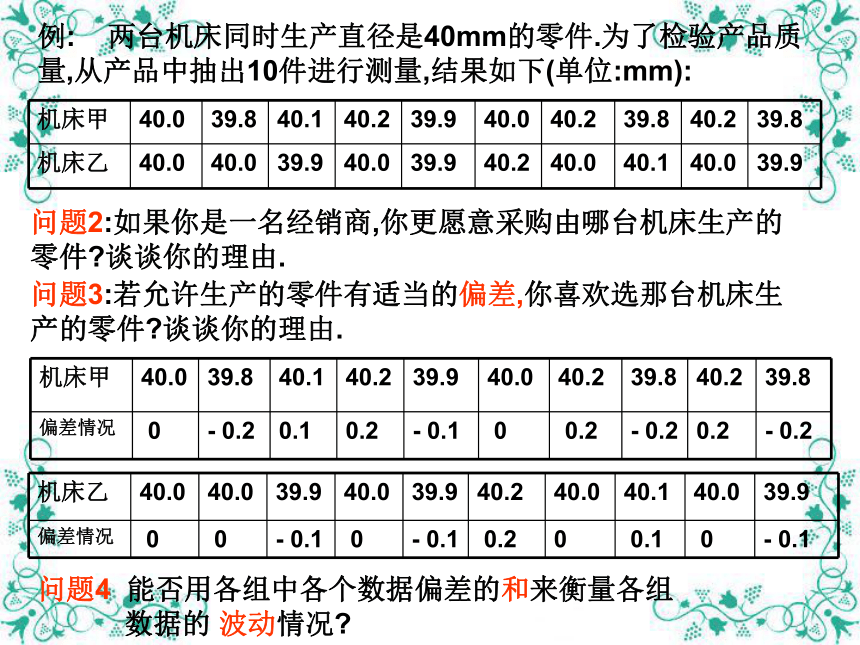
问题3:若允许生产的零件有适当的偏差,你喜欢选那台机床生产的零件?谈谈你的理由.
问题2:如果你是一名经销商,你更愿意采购由哪台机床生产的 零件?谈谈你的理由.
问题4 能否用各组中各个数据偏差的和来衡量各组
数据的 波动情况?
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
偏差情况 0 - 0.2 0.1 0.2 - 0.1 0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
偏差情况 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
方差:各数据与平均数的差的平方的平均数叫做这批数据的方差.
=0.026
=0.008
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
偏差情况 0 - 0.2 0.1 0.2 - 0.1 0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
偏差情况 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
方差用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).
在样本容量相同的情况下,方差越大,说明数据的
波动越大,越不稳定.
方差:各数据与平均数的差的平方的平均数叫做这批数据的方差.
例: 为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐?
思考:求数据方差的一般步骤是什么?
1、求数据的平均数;
2、利用方差公式求方差。
练习1:
某班有甲、乙两位同学,他们某学期的五次数学测验成绩如下(单位:分):
甲: 76、 84、 80、 87、 73
乙: 78、 82、 79、 80、 81
请问哪位同学的数学成绩比较稳定?
标准差: 方差的算术平方根.
问题:根据方差或标准差来比较两组数据的波动大小,必须在什么前提条件下?
两组数据的容量相同
练习2
C
2、为了选拔一名同学参加某市中学生射击竞赛,
某校对甲、乙两名同学的射击水平进行了测试,
两人在相同条件下各射靶10次.
?
①求方差S2乙;
②赛后,甲乙两个同学都说自己是胜者,争执不下.请你根据所学过的统计知识,进一步判断甲乙两个同学在这次测试中成绩谁优谁次,并说明理由。
S2乙=1.2
甲成绩
(环数) 7 8 6 8 6 5 9 10 7 4
=7 S2 甲=3
乙成绩
(环数) 9 5 7 8 7 6 8 6 7 7
=7 S2乙=?
小结:谈谈自己这节课你学到什么?
1.方差:各数据与平均数的差的平方的平均数叫做这 批数据的方差.
2.方差用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
3.标准差:方差的算术平方根叫做标准差.
例: 两台机床同时生产直径是40mm的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:mm):
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
以40为基准 0.0 - 0.2 0.1 0.2 - 0.1 0.0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
以40为基准 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
方差的简化计算
例1:计算下面一组数据的方差(结果精确到0.1):
5 4 4 3 4
3 2 3 5 3
方差和标准差
例: 两台机床同时生产直径是40mm的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:mm):
问题1:请计算这两组数据的平均数.
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
以40为基准 0.0 - 0.2 0.1 0.2 - 0.1 0.0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
以40为基准 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
例: 两台机床同时生产直径是40mm的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:mm):
问题3:若允许生产的零件有适当的偏差,你喜欢选那台机床生产的零件?谈谈你的理由.
问题2:如果你是一名经销商,你更愿意采购由哪台机床生产的 零件?谈谈你的理由.
问题4 能否用各组中各个数据偏差的和来衡量各组
数据的 波动情况?
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
偏差情况 0 - 0.2 0.1 0.2 - 0.1 0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
偏差情况 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
方差:各数据与平均数的差的平方的平均数叫做这批数据的方差.
=0.026
=0.008
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
偏差情况 0 - 0.2 0.1 0.2 - 0.1 0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
偏差情况 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
方差用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).
在样本容量相同的情况下,方差越大,说明数据的
波动越大,越不稳定.
方差:各数据与平均数的差的平方的平均数叫做这批数据的方差.
例: 为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐?
思考:求数据方差的一般步骤是什么?
1、求数据的平均数;
2、利用方差公式求方差。
练习1:
某班有甲、乙两位同学,他们某学期的五次数学测验成绩如下(单位:分):
甲: 76、 84、 80、 87、 73
乙: 78、 82、 79、 80、 81
请问哪位同学的数学成绩比较稳定?
标准差: 方差的算术平方根.
问题:根据方差或标准差来比较两组数据的波动大小,必须在什么前提条件下?
两组数据的容量相同
练习2
C
2、为了选拔一名同学参加某市中学生射击竞赛,
某校对甲、乙两名同学的射击水平进行了测试,
两人在相同条件下各射靶10次.
?
①求方差S2乙;
②赛后,甲乙两个同学都说自己是胜者,争执不下.请你根据所学过的统计知识,进一步判断甲乙两个同学在这次测试中成绩谁优谁次,并说明理由。
S2乙=1.2
甲成绩
(环数) 7 8 6 8 6 5 9 10 7 4
=7 S2 甲=3
乙成绩
(环数) 9 5 7 8 7 6 8 6 7 7
=7 S2乙=?
小结:谈谈自己这节课你学到什么?
1.方差:各数据与平均数的差的平方的平均数叫做这 批数据的方差.
2.方差用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
3.标准差:方差的算术平方根叫做标准差.
例: 两台机床同时生产直径是40mm的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:mm):
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
机床甲 40.0 39.8 40.1 40.2 39.9 40.0 40.2 39.8 40.2 39.8
以40为基准 0.0 - 0.2 0.1 0.2 - 0.1 0.0 0.2 - 0.2 0.2 - 0.2
机床乙 40.0 40.0 39.9 40.0 39.9 40.2 40.0 40.1 40.0 39.9
以40为基准 0 0 - 0.1 0 - 0.1 0.2 0 0.1 0 - 0.1
方差的简化计算
例1:计算下面一组数据的方差(结果精确到0.1):
5 4 4 3 4
3 2 3 5 3
