六年级下册数学一课一练-4.1圆柱和圆锥 冀教版 (含答案)
文档属性
| 名称 | 六年级下册数学一课一练-4.1圆柱和圆锥 冀教版 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 60.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 20:24:57 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学一课一练-4.1圆柱和圆锥
一、单选题
1.一个圆柱底面直径是16cm,高是16cm,它的侧面积展开是( )
A.?圆形???????????????????????????????B.?长方形???????????????????????????????C.?正方形???????????????????????????????D.?平行四边形
2.圆柱的侧面是(?? )
A.?平面??????????????????????????????????????????B.?曲面??????????????????????????????????????????C.?圆
3.油漆圆柱形柱子,要计算油漆的面积有多大,就是求(? )
A.?体积???????????????????????????????????????B.?表面积???????????????????????????????????????C.?侧面积
4.一个圆柱的底面半径是4cm,高是25.12cm,它的侧面沿高剪开是(?? )
A.?长方形???????????????????????????????????B.?正方形???????????????????????????????????C.?平行四边形
二、判断题
5.从圆锥的顶点到底面周长任意一点的连线都是圆锥的高.( ??)
6.一个圆锥的底面半径扩大3倍,高缩小9倍,圆锥的体积不变。
7.圆锥的底面半径扩大到原来的3倍,高不变,体积也扩大到原来的3倍。
8.在棱长是6分米的正方体中,削一个最大的圆柱,这个圆柱的底面直径和高都是6分米.(判断对错)
9.一个圆锥的底面半径扩大3倍,高不变,它的体积就扩大9倍。
三、填空题
10.圆柱的________加上________就是圆柱的表面积。
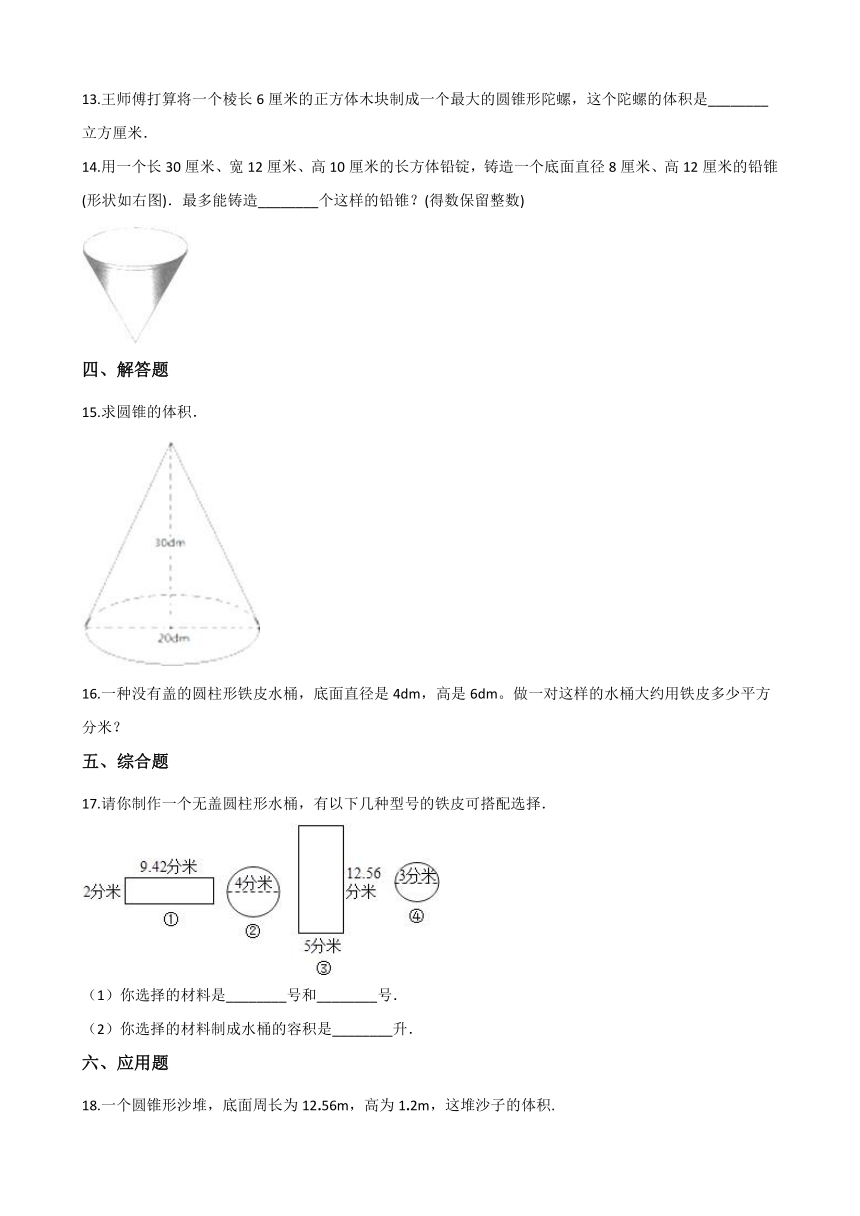
11.下面几号图旋转可以成圆柱体________,几号图旋转可以成圆锥体________.
A、 B、 C、 D、 E、
12.把图1中的正方形绕一条边旋转一周,所形成圆柱的侧面积是________.图2的三角形绕一条直角边旋转一周,所形成的圆锥的体积是________立方厘米.
13.王师傅打算将一个棱长6厘米的正方体木块制成一个最大的圆锥形陀螺,这个陀螺的体积是________立方厘米.
14.用一个长30厘米、宽12厘米、高10厘米的长方体铅锭,铸造一个底面直径8厘米、高12厘米的铅锥(形状如右图).最多能铸造________个这样的铅锥?(得数保留整数)
四、解答题
15.求圆锥的体积.
16.一种没有盖的圆柱形铁皮水桶,底面直径是4dm,高是6dm。做一对这样的水桶大约用铁皮多少平方分米?
五、综合题
17.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可搭配选择.
(1)你选择的材料是________号和________号.
(2)你选择的材料制成水桶的容积是________升.
六、应用题
18.一个圆锥形沙堆,底面周长为12.56m,高为1.2m,这堆沙子的体积.
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:因为圆柱的底面周长3.14×16=50.24厘米,高是16厘米,
底面周长大于高,
所以它的侧面展开是一个长方形;
故选:B.
【分析】根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”,若底面周长与高相等,则是一个正方形,据此进行分析解答即可.
2.【答案】 B
【解析】【解答】解:根据分析可知:圆柱的侧面是曲面;
故选:B.
【分析】根据圆柱的特征及对圆柱的了解可知:圆柱的侧面是曲面,圆柱的上下两个面是圆;由此进行解答即可.
3.【答案】C
【解析】【解答】油漆圆柱形柱子,要计算油漆的面积有多大,就是求圆柱的侧面积。
【分析】由于圆柱形柱子的上下底面不外露,所以求圆柱的侧面积.据此解答。
故选:C
4.【答案】 B
【解析】【解答】解:由题意知,圆柱的底面周长为:2×3.14×4=25.12(厘米),与高25.12厘米相等,
所以它的侧面沿高剪开是正方形;
故选:B.
【分析】根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”进行分析:如果该圆柱侧面展开是正方形,则圆柱的高等于圆柱的底面周长,圆柱的底面是一个圆,根据“圆的周长=2πr”进行解答即可.
二、判断题
5.【答案】 错误
【解析】【解答】 从圆锥的顶点到底面圆心的距离是圆锥的高,原题说法错误.
故答案为:错误.
【分析】 根据圆锥体的高的定义可知:从圆锥顶点到底面圆中心的距离叫做圆锥的高,据此判断.
6.【答案】正确
【解析】解答:
分析:由圆锥的体积公式即可得。
7.【答案】错误
【解析】【解答】解:底面半径扩大到原来的3倍,底面积就会扩大9倍,高不变,体积扩大到原来的9倍.原题说法错误.
故答案为:错误
【分析】圆锥的体积=底面积×高×,高不变,圆锥的体积扩大的倍数与底面积扩大的倍数相同,因此只需要判断出底面积扩大的倍数即可.
8.【答案】正确
【解析】【解答】解:圆柱的底面直径和高都等于正方体的棱长,即都是6分米, 故题干的说法是正确的.
故答案为:正确.
【分析】把正方体削成一个最大的圆柱,那么圆柱的底面直径和高都等于正方体的棱长,依此即可求解.
9.【答案】 正确
【解析】解答:圆锥的底面是圆,因为半径扩大3倍,圆的面积就扩大3×3=9倍,所以一个圆锥的底面半径扩大3倍,高不变,它的体积就扩大9倍。
故答案为正确
分析:根据圆锥的体积公式:V= sh , 因为圆锥的底面是一个圆,由圆的面积公式:s=πr? , 半径扩大3倍,圆的面积就扩大3×3=9倍,由此解答。
三、填空题
10.【答案】侧面积 ;两个底面面积
【解析】【解答】圆柱的底面面积加上侧面积就是圆柱的表面积。
【分析】圆柱的表面积。
11.【答案】B;D
【解析】【解答】A、性质后上面是圆柱,下面是圆锥;
B、旋转后得到一个圆柱;
C、旋转后得到两个底面重合的圆锥;
D、旋转后得到一个圆锥;
E、旋转后得到一个立体图形,这个图形既不是圆柱也不是圆锥.
故答案为:B;D
【分析】沿着长方形的一条边旋转后会得到一个圆柱;沿着直角三角形的一条直角边旋转后会得到一个圆锥.
12.【答案】157平方分米;
【解析】【解答】解:①圆柱的侧面积:
2×3.14×5×5
=6.28×25
=157(平方分米);
②圆锥的体积:
×π×a2×a
= (立方厘米);
故答案为:157平方分米, .
【分析】把图1中的正方形绕一条边旋转一周,所形成圆柱底面半径是5分米,高是5分米,要求它的侧面积是多少,根据圆柱的侧面积S=2πrh解答即可;图2的三角形绕一条直角边旋转一周,所形成的圆锥底面半径是a厘米,高是a厘米,要求它的体积是多少,根据圆锥的体积公式v= sh解答即可.此题考查的目的是理解圆柱、圆锥的特征,掌握圆柱侧面积、圆锥体积的计算方法.
13.【答案】56.52
【解析】【解答】解: ×3.14× ×6,
= ×3.14×9×6,
=56.52(立方厘米);
答:这个陀螺的体积是56.52立方厘米.
故答案为:56.52.
【分析】正方体内最大的圆锥的底面直径和高都等于正方体的棱长6厘米,由此利用圆锥的体积公式即可解答.此题考查圆锥的体积公式的计算应用,计算时不要漏乘 ,关键是根据正方体内最大的圆锥的特点得出它的底面直径和高.
14.【答案】17
【解析】【解答】30×12×10
=360×10
=3600(立方厘米)
8÷2=4(厘米)
×3.14×42×12
=×3.14×16×12
=3.14×16×4
=50.24×4
=200.96(立方厘米)
3600÷200.96≈17(个)
故答案为:17.
【分析】根据题意,先求出这个长方体铅锭的体积,用公式:V=abh,然后求出一个铅锥的体积,用公式:V=πr2 , 最后用长方体的体积÷圆锥的体积=制作的个数,据此列式解答.
四、解答题
15.【答案】圆锥的体积是3140立方分米
【解析】【解答】解: ×3.14× 2×30
= ×3.14×100×30
=3140(立方分米)
答:圆锥的体积是3140立方分米。
【分析】根据圆锥的体积公式:v= sh , 把数据代入公式解答。
16.【答案】解:3.14×(4÷2)?+3.14×4×6
=3.14×4+3.14×24
=3.14×28
=87.92(dm?)
87.92×2=175.84(dm?)
答:做一对这样的水桶大约需要用铁皮175.84平方分米.
【解析】【分析】用圆柱形水桶的底面积加上侧面积即可求出一个水桶需要铁皮的面积,再乘2即可;圆柱的侧面积=底面周长×高.
五、综合题
17.【答案】 (1)②;③
(2)62.8
【解析】【解答】解:(1)材料②的周长3.14×4=12.56(分米),
材料④的周长3.14×3=9.42(分米),
所以要选材料②、③;
故答案为:②,③;
2)制作成水桶的底面直径是4分米,高是5分米;
水桶的容积:
3.14×(4÷2)2×5,
=3.14×22×5,
=3.14×4×5,
=62.8(立方分米),
62.8立方分米=62.8升,
答:水桶的容积为62.8升.
【分析】(1)制作圆柱形水桶,说明要选一个长方形和一个圆形铁皮,而且所选的长方形的一条边和圆的周长相等即可达到要求,关键算出圆的周长;(2)由上面提供的数据直接运用圆柱的体积计算公式列式解决问题.此题主要考查圆柱的展开图以及利用圆柱的体积计算公式解答问题.
六、应用题
18.【答案】解: ?
答:这堆沙子的体积是5.024立方米.
【解析】【分析】用底面周长除以3.14,再除以2求出底面半径,然后用圆锥的底面积乘高,再乘即可求出沙子的体积.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学一课一练-4.1圆柱和圆锥
一、单选题
1.一个圆柱底面直径是16cm,高是16cm,它的侧面积展开是( )
A.?圆形???????????????????????????????B.?长方形???????????????????????????????C.?正方形???????????????????????????????D.?平行四边形
2.圆柱的侧面是(?? )
A.?平面??????????????????????????????????????????B.?曲面??????????????????????????????????????????C.?圆
3.油漆圆柱形柱子,要计算油漆的面积有多大,就是求(? )
A.?体积???????????????????????????????????????B.?表面积???????????????????????????????????????C.?侧面积
4.一个圆柱的底面半径是4cm,高是25.12cm,它的侧面沿高剪开是(?? )
A.?长方形???????????????????????????????????B.?正方形???????????????????????????????????C.?平行四边形
二、判断题
5.从圆锥的顶点到底面周长任意一点的连线都是圆锥的高.( ??)
6.一个圆锥的底面半径扩大3倍,高缩小9倍,圆锥的体积不变。
7.圆锥的底面半径扩大到原来的3倍,高不变,体积也扩大到原来的3倍。
8.在棱长是6分米的正方体中,削一个最大的圆柱,这个圆柱的底面直径和高都是6分米.(判断对错)
9.一个圆锥的底面半径扩大3倍,高不变,它的体积就扩大9倍。
三、填空题
10.圆柱的________加上________就是圆柱的表面积。
11.下面几号图旋转可以成圆柱体________,几号图旋转可以成圆锥体________.
A、 B、 C、 D、 E、
12.把图1中的正方形绕一条边旋转一周,所形成圆柱的侧面积是________.图2的三角形绕一条直角边旋转一周,所形成的圆锥的体积是________立方厘米.
13.王师傅打算将一个棱长6厘米的正方体木块制成一个最大的圆锥形陀螺,这个陀螺的体积是________立方厘米.
14.用一个长30厘米、宽12厘米、高10厘米的长方体铅锭,铸造一个底面直径8厘米、高12厘米的铅锥(形状如右图).最多能铸造________个这样的铅锥?(得数保留整数)
四、解答题
15.求圆锥的体积.
16.一种没有盖的圆柱形铁皮水桶,底面直径是4dm,高是6dm。做一对这样的水桶大约用铁皮多少平方分米?
五、综合题
17.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可搭配选择.
(1)你选择的材料是________号和________号.
(2)你选择的材料制成水桶的容积是________升.
六、应用题
18.一个圆锥形沙堆,底面周长为12.56m,高为1.2m,这堆沙子的体积.
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:因为圆柱的底面周长3.14×16=50.24厘米,高是16厘米,
底面周长大于高,
所以它的侧面展开是一个长方形;
故选:B.
【分析】根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”,若底面周长与高相等,则是一个正方形,据此进行分析解答即可.
2.【答案】 B
【解析】【解答】解:根据分析可知:圆柱的侧面是曲面;
故选:B.
【分析】根据圆柱的特征及对圆柱的了解可知:圆柱的侧面是曲面,圆柱的上下两个面是圆;由此进行解答即可.
3.【答案】C
【解析】【解答】油漆圆柱形柱子,要计算油漆的面积有多大,就是求圆柱的侧面积。
【分析】由于圆柱形柱子的上下底面不外露,所以求圆柱的侧面积.据此解答。
故选:C
4.【答案】 B
【解析】【解答】解:由题意知,圆柱的底面周长为:2×3.14×4=25.12(厘米),与高25.12厘米相等,
所以它的侧面沿高剪开是正方形;
故选:B.
【分析】根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”进行分析:如果该圆柱侧面展开是正方形,则圆柱的高等于圆柱的底面周长,圆柱的底面是一个圆,根据“圆的周长=2πr”进行解答即可.
二、判断题
5.【答案】 错误
【解析】【解答】 从圆锥的顶点到底面圆心的距离是圆锥的高,原题说法错误.
故答案为:错误.
【分析】 根据圆锥体的高的定义可知:从圆锥顶点到底面圆中心的距离叫做圆锥的高,据此判断.
6.【答案】正确
【解析】解答:
分析:由圆锥的体积公式即可得。
7.【答案】错误
【解析】【解答】解:底面半径扩大到原来的3倍,底面积就会扩大9倍,高不变,体积扩大到原来的9倍.原题说法错误.
故答案为:错误
【分析】圆锥的体积=底面积×高×,高不变,圆锥的体积扩大的倍数与底面积扩大的倍数相同,因此只需要判断出底面积扩大的倍数即可.
8.【答案】正确
【解析】【解答】解:圆柱的底面直径和高都等于正方体的棱长,即都是6分米, 故题干的说法是正确的.
故答案为:正确.
【分析】把正方体削成一个最大的圆柱,那么圆柱的底面直径和高都等于正方体的棱长,依此即可求解.
9.【答案】 正确
【解析】解答:圆锥的底面是圆,因为半径扩大3倍,圆的面积就扩大3×3=9倍,所以一个圆锥的底面半径扩大3倍,高不变,它的体积就扩大9倍。
故答案为正确
分析:根据圆锥的体积公式:V= sh , 因为圆锥的底面是一个圆,由圆的面积公式:s=πr? , 半径扩大3倍,圆的面积就扩大3×3=9倍,由此解答。
三、填空题
10.【答案】侧面积 ;两个底面面积
【解析】【解答】圆柱的底面面积加上侧面积就是圆柱的表面积。
【分析】圆柱的表面积。
11.【答案】B;D
【解析】【解答】A、性质后上面是圆柱,下面是圆锥;
B、旋转后得到一个圆柱;
C、旋转后得到两个底面重合的圆锥;
D、旋转后得到一个圆锥;
E、旋转后得到一个立体图形,这个图形既不是圆柱也不是圆锥.
故答案为:B;D
【分析】沿着长方形的一条边旋转后会得到一个圆柱;沿着直角三角形的一条直角边旋转后会得到一个圆锥.
12.【答案】157平方分米;
【解析】【解答】解:①圆柱的侧面积:
2×3.14×5×5
=6.28×25
=157(平方分米);
②圆锥的体积:
×π×a2×a
= (立方厘米);
故答案为:157平方分米, .
【分析】把图1中的正方形绕一条边旋转一周,所形成圆柱底面半径是5分米,高是5分米,要求它的侧面积是多少,根据圆柱的侧面积S=2πrh解答即可;图2的三角形绕一条直角边旋转一周,所形成的圆锥底面半径是a厘米,高是a厘米,要求它的体积是多少,根据圆锥的体积公式v= sh解答即可.此题考查的目的是理解圆柱、圆锥的特征,掌握圆柱侧面积、圆锥体积的计算方法.
13.【答案】56.52
【解析】【解答】解: ×3.14× ×6,
= ×3.14×9×6,
=56.52(立方厘米);
答:这个陀螺的体积是56.52立方厘米.
故答案为:56.52.
【分析】正方体内最大的圆锥的底面直径和高都等于正方体的棱长6厘米,由此利用圆锥的体积公式即可解答.此题考查圆锥的体积公式的计算应用,计算时不要漏乘 ,关键是根据正方体内最大的圆锥的特点得出它的底面直径和高.
14.【答案】17
【解析】【解答】30×12×10
=360×10
=3600(立方厘米)
8÷2=4(厘米)
×3.14×42×12
=×3.14×16×12
=3.14×16×4
=50.24×4
=200.96(立方厘米)
3600÷200.96≈17(个)
故答案为:17.
【分析】根据题意,先求出这个长方体铅锭的体积,用公式:V=abh,然后求出一个铅锥的体积,用公式:V=πr2 , 最后用长方体的体积÷圆锥的体积=制作的个数,据此列式解答.
四、解答题
15.【答案】圆锥的体积是3140立方分米
【解析】【解答】解: ×3.14× 2×30
= ×3.14×100×30
=3140(立方分米)
答:圆锥的体积是3140立方分米。
【分析】根据圆锥的体积公式:v= sh , 把数据代入公式解答。
16.【答案】解:3.14×(4÷2)?+3.14×4×6
=3.14×4+3.14×24
=3.14×28
=87.92(dm?)
87.92×2=175.84(dm?)
答:做一对这样的水桶大约需要用铁皮175.84平方分米.
【解析】【分析】用圆柱形水桶的底面积加上侧面积即可求出一个水桶需要铁皮的面积,再乘2即可;圆柱的侧面积=底面周长×高.
五、综合题
17.【答案】 (1)②;③
(2)62.8
【解析】【解答】解:(1)材料②的周长3.14×4=12.56(分米),
材料④的周长3.14×3=9.42(分米),
所以要选材料②、③;
故答案为:②,③;
2)制作成水桶的底面直径是4分米,高是5分米;
水桶的容积:
3.14×(4÷2)2×5,
=3.14×22×5,
=3.14×4×5,
=62.8(立方分米),
62.8立方分米=62.8升,
答:水桶的容积为62.8升.
【分析】(1)制作圆柱形水桶,说明要选一个长方形和一个圆形铁皮,而且所选的长方形的一条边和圆的周长相等即可达到要求,关键算出圆的周长;(2)由上面提供的数据直接运用圆柱的体积计算公式列式解决问题.此题主要考查圆柱的展开图以及利用圆柱的体积计算公式解答问题.
六、应用题
18.【答案】解: ?
答:这堆沙子的体积是5.024立方米.
【解析】【分析】用底面周长除以3.14,再除以2求出底面半径,然后用圆锥的底面积乘高,再乘即可求出沙子的体积.
