六年级下册数学单元测试-2.圆柱和圆锥 青岛版(含答案)
文档属性
| 名称 | 六年级下册数学单元测试-2.圆柱和圆锥 青岛版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 90.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-18 20:30:01 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学单元测试-2.圆柱和圆锥
一、单选题
1.一个圆柱的底面直径和高都扩大到原来的2倍,它的体积扩大到原来的(?? )
A.?2倍???????????????????????????????????????????B.?4倍???????????????????????????????????????????C.?8倍
2.下面图(? )恰好可以围成圆柱体.(接头忽略不计,单位:厘米)
A.?????????????????????????B.?
C.?????????????????????????????????????????????????D.?
3.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱高的3倍,圆锥的体积是12立方分米,圆柱的体积是(??? )立方分米。
A.?12?????????????????????????????????????????B.?4?????????????????????????????????????????C.?8?????????????????????????????????????????D.?36??
4.一个圆柱体的侧面展开是一个正方形,底面直径是4分米,高是(? )
A.?4分米????????????????????????????????B.?12.56平方分米????????????????????????????????C.?12.56分米
二、判断题
5.一个圆柱给出了底面半径,我能求出该圆柱的侧面积。
?
6.判断对错
圆柱体、长方体、正方体的底面积和高都相等,它们的体积也相等.
7.判断正误.
观察一个圆柱体的木块,它的侧面有可能是一个正方形.
8.圆锥体积等于和它等底等高的圆柱体积的 .(判断对错)
三、填空题
9.计算出下列圆柱的侧面积.
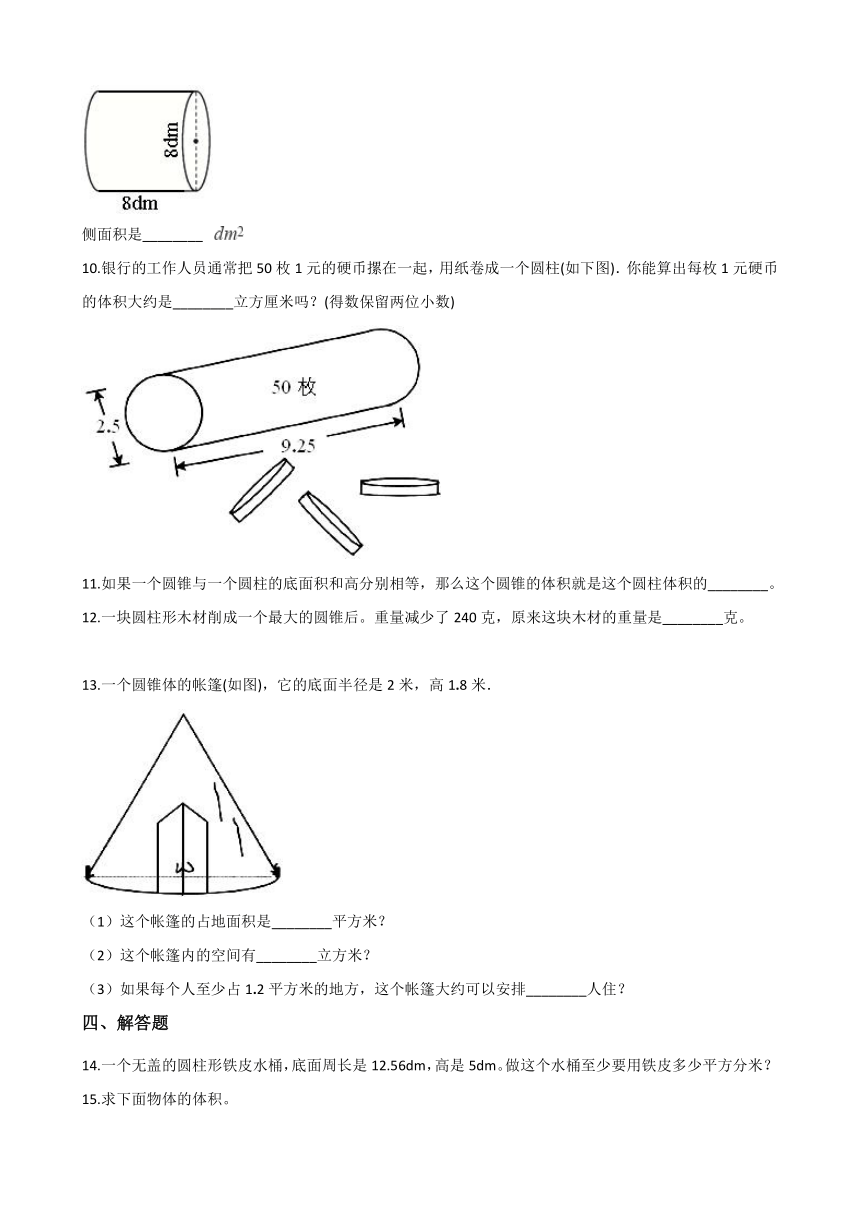
侧面积是________? ?
10.银行的工作人员通常把50枚1元的硬币摞在一起,用纸卷成一个圆柱(如下图).你能算出每枚1元硬币的体积大约是________立方厘米吗?(得数保留两位小数)
11.如果一个圆锥与一个圆柱的底面积和高分别相等,那么这个圆锥的体积就是这个圆柱体积的________。
12.一块圆柱形木材削成一个最大的圆锥后。重量减少了240克,原来这块木材的重量是________克。
13.一个圆锥体的帐篷(如图),它的底面半径是2米,高1.8米.
(1)这个帐篷的占地面积是________平方米?
(2)这个帐篷内的空间有________立方米?
(3)如果每个人至少占1.2平方米的地方,这个帐篷大约可以安排________人住?
四、解答题
14.一个无盖的圆柱形铁皮水桶,底面周长是12.56dm,高是5dm。做这个水桶至少要用铁皮多少平方分米?
15.求下面物体的体积。
五、综合题
16.一个圆锥形的沙堆,量得底面积是28平方米,高1.5米.
(1)如果每立方米沙重1.5吨,这堆沙重多少吨?
(2)用这堆沙配制水泥2份,沙3份,石子5份的混凝土,需水泥、石子各多少吨?
六、应用题
17.操场上运来的沙子堆成一个圆锥形,底面周长是12.56米,高是12分米,每立方米沙子约重1.7吨,这堆沙子一共重约多少吨?
18.一块长方体钢锭,底面周长是20分米,长与宽的比是4:1,高比宽少45%,它正好可以铸成高为6分米的圆锥体,圆锥体的底面积是多少平方分米?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】圆柱的底面直径扩大2倍,底面积扩大4倍,高扩大2倍,那么它的体积扩大4×2=8倍。
故答案为:C。
【分析】根据圆柱的体积公式:v=sh,圆柱的底面直径扩大2倍,底面积扩大4倍,高扩大2倍,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答。
2.【答案】A
【解析】【解答】A,因为3.14×(2÷1)=3.14,所以长方形的长等于底面周长;
B,因为3.14×(2÷1)=3.14,所以长方形的长不等于底面周长;
C,因为3.14×(2÷1)=3.14,所以长方形的不长等于底面周长;
D,因为3.14×(2÷1)=3.14,所以长方形的长不等于底面周长;
【分析】依据圆柱的侧面展开图的特点可知:圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,据此利用题目中的数据,计算后即可得解。
故选:A
3.【答案】 A
【解析】【解答】解:设圆柱的体积是=S。
圆锥的体积V=Sh,当h=3×时,V=S=12,故V=。
故答案为:A。
【分析】一个圆柱和一个圆锥的底面直径相等,说明两个图形的底面积相等;由于底面积相等,比较两个图形的大小就取决于高,圆锥的高是圆柱高的3倍,这样圆锥的体积=圆柱的体积××3,故圆锥体积=圆柱体积。
4.【答案】 C
【解析】【解答】解:根据题意,可知圆柱的高=圆柱的底面周长,
圆柱的高是:3.14×4=12.56(分米);
答:圆柱的高是12.56分米.
故选:C.
【分析】根据一个圆柱体的侧面展开是一个正方形,可知这个圆柱的底面周长和高相等,要求高是多少,用圆周率乘直径求得底面周长即可.此题考查圆柱的展开图,圆柱体的侧面沿高线剪开是一个长方形或正方形,剪开后如果是正方形,说明此圆柱的底面周长和高相等;剪开后是长方形,说明圆柱的底面周长和高不相等.
二、判断题
5.【答案】错误
【解析】【解答】圆柱的侧面积等于底面周长乘以高。
【分析】圆柱的侧面积等于底面周长乘以高,本题只给出了底面半径,所以无法求出侧面积。
6.【答案】正确
【解析】圆柱体,正方体,长方体的体积公式有什么共性? 解:由于柱体的体积都可以写成:
底面积×高
所以在圆柱体、长方体、正方体的底面积和高都相等时,它们的体积也相等.
答案为T
7.【答案】 正确
【解析】【解答】观察一个圆柱体的木块,它的侧面有可能是一个正方形,也可能是一个长方形,原题说法正确.
故答案为:正确.
【分析】观察一个圆柱体的木块,它的侧面有可能是一个正方形,也可能是一个长方形,据此解答.
8.【答案】 正确
【解析】【解答】解:根据圆柱和圆锥的体积公式可知,圆锥的体积等于和它等底等高的圆柱体积的,原题说法正确.
故答案为:正确
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,由此根据体积公式判断体积之间的关系即可.
三、填空题
9.【答案】200.96
【解析】【解答】3.14×8×8=3.14×64=200.96(dm?)
故答案为:200.96
【分析】圆柱的侧面积=底面周长×高,由此根据圆柱的侧面积公式计算侧面积即可.
10.【答案】 0.91
【解析】【解答】3.14×(2.5÷2)2×9.25÷50≈0.91(立方厘米)
【分析】首先根据圆柱的体积=底面积×高求出50枚硬币的体积是多少,然后再除以50就是每枚硬币的体积。
11.【答案】
【解析】【解答】根据圆柱的体积公式V=sh,圆锥的体积公式V=?sh。底面积和高分别相等,圆锥的体积就是圆柱体积的。
故答案为:。
【分析】根据圆柱的体积公式和圆锥的体积公式即可求解。
12.【答案】 360
【解析】【解答】解:240÷2×3=360(克)
故答案为:360
【分析】这个圆锥和圆柱等底等高,圆柱的体积是圆锥体积的3倍,圆锥是1份,圆柱就是3份,削去的是2份,重量减少的是2份的重量,因此先求出1份的重量,再乘3就是总重量.
13.【答案】(1)12.56
(2)7.536
(3)10
【解析】【解答】(1)3.14×22
=3.14×4
=12.56(平方米)
(2)×12.56×1.8
=12.56×0.6
=7.536(立方米)
(3)12.56÷1.2≈10(人)
故答案为:(1)12.56;(2)7.536;(3)10.
【分析】已知圆锥的底面半径r和高h,求底面积,用公式:S=πr2 , 据此列式计算;要求圆锥的体积,用公式:V=Sh;要求够几个人居住,用圆锥的底面积÷每个人的占地面积=可以住的人数,据此解答.
四、解答题
14.【答案】解:(12.56÷3.14÷2)2×3.14+12.56×5
=4×3.14+62.8
=12.56+62.8
=75.36(dm2)
答:做这个水桶至少要用铁皮75.36平方分米.
【解析】【分析】用底面周长除以3.14再除以2求出底面半径,然后用底面积加上侧面积即可求出需要铁皮的面积,圆柱的侧面积=底面周长×高.
15.【答案】 解:3.14×(2÷2)2×4+3.14×(2÷2)2×3× =15.7(cm3)
【解析】【分析】图中是一个圆锥和圆柱的组合,故物体的体积=圆柱的体积+圆锥的体积,其中圆柱的体积=πr2h,圆锥的体积=πr2h,据此代入数据作答即可。
五、综合题
16.【答案】 (1)解: ×28×1.5×1.5,
=21(吨),
答:这堆沙重21吨.
(2)解:21÷ =70(吨),
所以水泥有:70× =14(吨),
石子有:70× =35(吨),
答:需要水泥14吨,石子35吨.
【解析】【分析】(1)要求这堆沙重多少吨,就必须先求出这沙堆的体积,也就是求出底面积是28平方米,高是1.5米的圆锥的体积,利用圆锥的体积= ×底面积×高,即可求得其体积,由此即可解决问题;(2)根据题干可得:水泥:沙子:石子=2:3:5,则沙子占的混凝土的 ,由此利用上面求出的沙子的重量,求出混凝土的总重量,再利用按比例分配的方法即可求出水泥和石子的重量.此题考查了圆锥的体积公式在实际问题中的灵活应用以及利用按比例分配解决问题的方法.
六、应用题
17.【答案】解:12分米=1.2米,
沙堆的底面积是:
3.14×(12.56÷3.14÷2)2 ,
=3.14×4,
=12.56(平方米);
这堆沙的重量是:
1.7×(12.56×1.2÷3),
=1.7×5.024,
=8.5408(吨);
答:这堆沙子一共重约8.5408吨.
【解析】【分析】先根据沙堆的底面周长12.56米求出底面积,再根据已求的底面积和高12分米(1.2米),求出沙堆的体积,最后根据每立方米沙子约重1.7吨,用乘法求得重量即可.解答此题的重点是求沙堆的体积,关键是求沙堆的底面积,要注意单位的统一.
18.【答案】解:底面的长与宽的和:20÷2=10(分米),
底面长:10× =8(分米),宽:10﹣8=2(分米),长方体高:2×(1﹣45%=1.1(分米);
长方体的体积:8×2×1.1=17.6(立方分米);
圆锥体的底面积:17.6×3÷6=52.8÷6=8.8(平方分米);
答:圆锥体的底面积是8.8平方分米.
【解析】【分析】根据底面周长先算出底面长和宽的和,再根据长与宽的比算出底面的长和宽是多少,高比宽少45%就是高是宽的(145%),根据分数乘法的意义即可算出高是多少,再根据长方形的体积公式进行计算即可算出长方体的体积。根据题意可知长方体和圆锥的体积相等,根据圆锥的底面积=圆锥的体积3圆锥的高即可算出圆锥的底面积
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学单元测试-2.圆柱和圆锥
一、单选题
1.一个圆柱的底面直径和高都扩大到原来的2倍,它的体积扩大到原来的(?? )
A.?2倍???????????????????????????????????????????B.?4倍???????????????????????????????????????????C.?8倍
2.下面图(? )恰好可以围成圆柱体.(接头忽略不计,单位:厘米)
A.?????????????????????????B.?
C.?????????????????????????????????????????????????D.?
3.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱高的3倍,圆锥的体积是12立方分米,圆柱的体积是(??? )立方分米。
A.?12?????????????????????????????????????????B.?4?????????????????????????????????????????C.?8?????????????????????????????????????????D.?36??
4.一个圆柱体的侧面展开是一个正方形,底面直径是4分米,高是(? )
A.?4分米????????????????????????????????B.?12.56平方分米????????????????????????????????C.?12.56分米
二、判断题
5.一个圆柱给出了底面半径,我能求出该圆柱的侧面积。
?
6.判断对错
圆柱体、长方体、正方体的底面积和高都相等,它们的体积也相等.
7.判断正误.
观察一个圆柱体的木块,它的侧面有可能是一个正方形.
8.圆锥体积等于和它等底等高的圆柱体积的 .(判断对错)
三、填空题
9.计算出下列圆柱的侧面积.
侧面积是________? ?
10.银行的工作人员通常把50枚1元的硬币摞在一起,用纸卷成一个圆柱(如下图).你能算出每枚1元硬币的体积大约是________立方厘米吗?(得数保留两位小数)
11.如果一个圆锥与一个圆柱的底面积和高分别相等,那么这个圆锥的体积就是这个圆柱体积的________。
12.一块圆柱形木材削成一个最大的圆锥后。重量减少了240克,原来这块木材的重量是________克。
13.一个圆锥体的帐篷(如图),它的底面半径是2米,高1.8米.
(1)这个帐篷的占地面积是________平方米?
(2)这个帐篷内的空间有________立方米?
(3)如果每个人至少占1.2平方米的地方,这个帐篷大约可以安排________人住?
四、解答题
14.一个无盖的圆柱形铁皮水桶,底面周长是12.56dm,高是5dm。做这个水桶至少要用铁皮多少平方分米?
15.求下面物体的体积。
五、综合题
16.一个圆锥形的沙堆,量得底面积是28平方米,高1.5米.
(1)如果每立方米沙重1.5吨,这堆沙重多少吨?
(2)用这堆沙配制水泥2份,沙3份,石子5份的混凝土,需水泥、石子各多少吨?
六、应用题
17.操场上运来的沙子堆成一个圆锥形,底面周长是12.56米,高是12分米,每立方米沙子约重1.7吨,这堆沙子一共重约多少吨?
18.一块长方体钢锭,底面周长是20分米,长与宽的比是4:1,高比宽少45%,它正好可以铸成高为6分米的圆锥体,圆锥体的底面积是多少平方分米?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】圆柱的底面直径扩大2倍,底面积扩大4倍,高扩大2倍,那么它的体积扩大4×2=8倍。
故答案为:C。
【分析】根据圆柱的体积公式:v=sh,圆柱的底面直径扩大2倍,底面积扩大4倍,高扩大2倍,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答。
2.【答案】A
【解析】【解答】A,因为3.14×(2÷1)=3.14,所以长方形的长等于底面周长;
B,因为3.14×(2÷1)=3.14,所以长方形的长不等于底面周长;
C,因为3.14×(2÷1)=3.14,所以长方形的不长等于底面周长;
D,因为3.14×(2÷1)=3.14,所以长方形的长不等于底面周长;
【分析】依据圆柱的侧面展开图的特点可知:圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,据此利用题目中的数据,计算后即可得解。
故选:A
3.【答案】 A
【解析】【解答】解:设圆柱的体积是=S。
圆锥的体积V=Sh,当h=3×时,V=S=12,故V=。
故答案为:A。
【分析】一个圆柱和一个圆锥的底面直径相等,说明两个图形的底面积相等;由于底面积相等,比较两个图形的大小就取决于高,圆锥的高是圆柱高的3倍,这样圆锥的体积=圆柱的体积××3,故圆锥体积=圆柱体积。
4.【答案】 C
【解析】【解答】解:根据题意,可知圆柱的高=圆柱的底面周长,
圆柱的高是:3.14×4=12.56(分米);
答:圆柱的高是12.56分米.
故选:C.
【分析】根据一个圆柱体的侧面展开是一个正方形,可知这个圆柱的底面周长和高相等,要求高是多少,用圆周率乘直径求得底面周长即可.此题考查圆柱的展开图,圆柱体的侧面沿高线剪开是一个长方形或正方形,剪开后如果是正方形,说明此圆柱的底面周长和高相等;剪开后是长方形,说明圆柱的底面周长和高不相等.
二、判断题
5.【答案】错误
【解析】【解答】圆柱的侧面积等于底面周长乘以高。
【分析】圆柱的侧面积等于底面周长乘以高,本题只给出了底面半径,所以无法求出侧面积。
6.【答案】正确
【解析】圆柱体,正方体,长方体的体积公式有什么共性? 解:由于柱体的体积都可以写成:
底面积×高
所以在圆柱体、长方体、正方体的底面积和高都相等时,它们的体积也相等.
答案为T
7.【答案】 正确
【解析】【解答】观察一个圆柱体的木块,它的侧面有可能是一个正方形,也可能是一个长方形,原题说法正确.
故答案为:正确.
【分析】观察一个圆柱体的木块,它的侧面有可能是一个正方形,也可能是一个长方形,据此解答.
8.【答案】 正确
【解析】【解答】解:根据圆柱和圆锥的体积公式可知,圆锥的体积等于和它等底等高的圆柱体积的,原题说法正确.
故答案为:正确
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,由此根据体积公式判断体积之间的关系即可.
三、填空题
9.【答案】200.96
【解析】【解答】3.14×8×8=3.14×64=200.96(dm?)
故答案为:200.96
【分析】圆柱的侧面积=底面周长×高,由此根据圆柱的侧面积公式计算侧面积即可.
10.【答案】 0.91
【解析】【解答】3.14×(2.5÷2)2×9.25÷50≈0.91(立方厘米)
【分析】首先根据圆柱的体积=底面积×高求出50枚硬币的体积是多少,然后再除以50就是每枚硬币的体积。
11.【答案】
【解析】【解答】根据圆柱的体积公式V=sh,圆锥的体积公式V=?sh。底面积和高分别相等,圆锥的体积就是圆柱体积的。
故答案为:。
【分析】根据圆柱的体积公式和圆锥的体积公式即可求解。
12.【答案】 360
【解析】【解答】解:240÷2×3=360(克)
故答案为:360
【分析】这个圆锥和圆柱等底等高,圆柱的体积是圆锥体积的3倍,圆锥是1份,圆柱就是3份,削去的是2份,重量减少的是2份的重量,因此先求出1份的重量,再乘3就是总重量.
13.【答案】(1)12.56
(2)7.536
(3)10
【解析】【解答】(1)3.14×22
=3.14×4
=12.56(平方米)
(2)×12.56×1.8
=12.56×0.6
=7.536(立方米)
(3)12.56÷1.2≈10(人)
故答案为:(1)12.56;(2)7.536;(3)10.
【分析】已知圆锥的底面半径r和高h,求底面积,用公式:S=πr2 , 据此列式计算;要求圆锥的体积,用公式:V=Sh;要求够几个人居住,用圆锥的底面积÷每个人的占地面积=可以住的人数,据此解答.
四、解答题
14.【答案】解:(12.56÷3.14÷2)2×3.14+12.56×5
=4×3.14+62.8
=12.56+62.8
=75.36(dm2)
答:做这个水桶至少要用铁皮75.36平方分米.
【解析】【分析】用底面周长除以3.14再除以2求出底面半径,然后用底面积加上侧面积即可求出需要铁皮的面积,圆柱的侧面积=底面周长×高.
15.【答案】 解:3.14×(2÷2)2×4+3.14×(2÷2)2×3× =15.7(cm3)
【解析】【分析】图中是一个圆锥和圆柱的组合,故物体的体积=圆柱的体积+圆锥的体积,其中圆柱的体积=πr2h,圆锥的体积=πr2h,据此代入数据作答即可。
五、综合题
16.【答案】 (1)解: ×28×1.5×1.5,
=21(吨),
答:这堆沙重21吨.
(2)解:21÷ =70(吨),
所以水泥有:70× =14(吨),
石子有:70× =35(吨),
答:需要水泥14吨,石子35吨.
【解析】【分析】(1)要求这堆沙重多少吨,就必须先求出这沙堆的体积,也就是求出底面积是28平方米,高是1.5米的圆锥的体积,利用圆锥的体积= ×底面积×高,即可求得其体积,由此即可解决问题;(2)根据题干可得:水泥:沙子:石子=2:3:5,则沙子占的混凝土的 ,由此利用上面求出的沙子的重量,求出混凝土的总重量,再利用按比例分配的方法即可求出水泥和石子的重量.此题考查了圆锥的体积公式在实际问题中的灵活应用以及利用按比例分配解决问题的方法.
六、应用题
17.【答案】解:12分米=1.2米,
沙堆的底面积是:
3.14×(12.56÷3.14÷2)2 ,
=3.14×4,
=12.56(平方米);
这堆沙的重量是:
1.7×(12.56×1.2÷3),
=1.7×5.024,
=8.5408(吨);
答:这堆沙子一共重约8.5408吨.
【解析】【分析】先根据沙堆的底面周长12.56米求出底面积,再根据已求的底面积和高12分米(1.2米),求出沙堆的体积,最后根据每立方米沙子约重1.7吨,用乘法求得重量即可.解答此题的重点是求沙堆的体积,关键是求沙堆的底面积,要注意单位的统一.
18.【答案】解:底面的长与宽的和:20÷2=10(分米),
底面长:10× =8(分米),宽:10﹣8=2(分米),长方体高:2×(1﹣45%=1.1(分米);
长方体的体积:8×2×1.1=17.6(立方分米);
圆锥体的底面积:17.6×3÷6=52.8÷6=8.8(平方分米);
答:圆锥体的底面积是8.8平方分米.
【解析】【分析】根据底面周长先算出底面长和宽的和,再根据长与宽的比算出底面的长和宽是多少,高比宽少45%就是高是宽的(145%),根据分数乘法的意义即可算出高是多少,再根据长方形的体积公式进行计算即可算出长方体的体积。根据题意可知长方体和圆锥的体积相等,根据圆锥的底面积=圆锥的体积3圆锥的高即可算出圆锥的底面积
