2020年春人教版数学八年级下册课件19.3课题学习选择方案(18张PPT)
文档属性
| 名称 | 2020年春人教版数学八年级下册课件19.3课题学习选择方案(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览





文档简介
课件18张PPT。?第十九章一次函数19.3 课题学习 选择方案核心目标进一步巩固一次函数的相关知识,能根据所列函数的解析式的性质,选择合理的方案解决问题.课前学案1.某水库的水位在5小时内持续上涨,初始的水位高度为
6米,水位以每小时0.3米的速度匀速上升,则水库的水
位高度y米与时间x小时(0≤x≤5)的函数关系式为_______
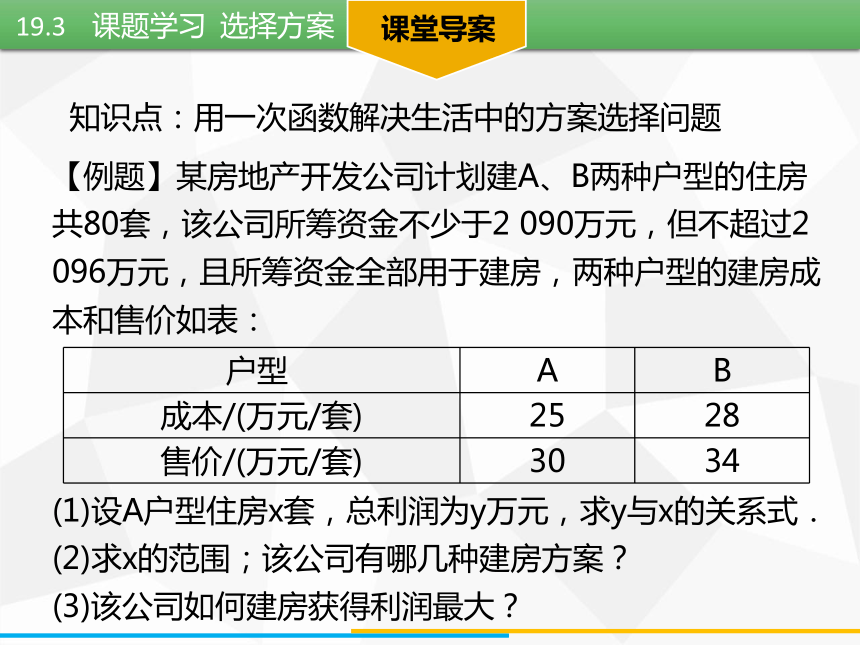
________________.2y=6+0.3x课堂导案知识点:用一次函数解决生活中的方案选择问题【例题】某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2 090万元,但不超过2 096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如表:
(1)设A户型住房x套,总利润为y万元,求y与x的关系式.
(2)求x的范围;该公司有哪几种建房方案?
(3)该公司如何建房获得利润最大?课堂导案(3)y=-x+480,y随x的增大而减小,
当x最小时,y取最大值,
当x=48时,y最大=-48+480=432(万元),
答:公司建48套A户型,32套B户型房获得利润
最大,最大利润是432万元.课堂导案课堂导案【解析】(1)根据户A型的利润与B户型的利润和, 可得函数关系式;
(2)根据A户型B户型的投资不少于2 090万元,但不超过2 096万元,可得不等式组,根据解不等式组,可得方案;
(3)根据一次函数的增减性,可得答案.【点拔】本题考查了一次函数的应用,(1)A户型与B户型的利润和是解题关键;(2)解不等式组是解题关键;(3)k<0时,y随x的增大而减小是解题关键.课堂导案1.学校组织暑期夏令营,学校联系了报价均为每人
200元的两家旅行社,经协商,甲旅行社的优惠
条件是:全部师生7.5折优惠;乙旅行社的优惠条
件是:可免去一位老师的费用,其余师生8折优惠.
(1)分别写出两家旅行社所需的费用y(元)与师生人
数x(人)的函数关系式;对点训练(1)y甲=150x, y乙=160x-160课堂导案(2)学校应选择哪家旅行社?(2)当y甲>y乙时,150x>160x-160得x<16 ;
当y甲=y乙时,x=16;当y甲<y乙时,x>16.
所以当x>16时应选择甲旅行社,
当x<16时,应选择乙旅行社,
当x=16时两家旅行社一样.课堂导案2.实验学校计划组织共青团员372人到某爱国主义
基地接受教育,并安排8位老师同行,经学校与
汽车出租公司协商,有两种型号客车可供选择,
它们的载客量和租金如下表,
为了保证每人都有座位,学校决定租8辆车.课堂导案(1)写出符合要求的租车方案,并说明理由;
(1)设租甲种客车x辆,则50x+30(8-x)≥372+8
得x≥7又x≤8即7≤x≤8 ∴x=7或8,
所以有两种租车方案:
方案一:租甲种客车7辆,乙种客车1辆;
方案二:租甲种客车8辆,乙种客车0辆.课堂导案(2)设租甲种客车x辆,总租金共y(元),写出y与x
之间的函数关系式;
(2)y=400x+200(8-x)
即y=200x+1 600;
(3)在(1)方案中,求出租金最少的租车方案.
(3)当x=7时,y=3 000;当x=8时,y=3 200,
所以租金最少的方案是租甲种客车7辆,乙种客
车1辆.课后练案3.康乐公司在A、B两地分别有同型号的机器17台和
15台,现要运往甲地18台,乙地14台,从A、
B两地运往甲、乙两地的价格如下表:
(1)如果从A地运往甲地x台,求完成以上调运所需
总费用y(元)与x(台)的函数关系式;(1)y=600x+500(17-x)+400(18-x)+800(x-3)
=500x+13 300;课后练案(2)若康乐公司请你设计一种最佳调运方案,使总的费
用最少,该公司完成以上调运方案至少需要多少费
用?这什么?(2)由(1)知总运费y=500x+13 300,
∵x≥0,17-x≥0,18-x≥0,x-3≥0
∴3≤x≤17又∵k>0 ∴y随x的增大而增大,
∴当x=3时,y最小=500×3+13 300=14 800(元),
所以完成以上调运方案至少需用14 800元运费,
最佳方案是:由A调3台至甲地,14台至乙地;由B调
15台至甲地.拓展提升4.抗震救灾中,某县粮食局为了保证库存粮食的安全,
决定将甲、乙两个仓库的粮食,全部转移到具有较
强抗震功能的A、B两仓库.已知甲库有粮食100吨,
乙库有粮食80吨,而A库的容量为70吨,B库的容量
为110吨.从甲、乙两库到A、B两库的路程和运费
如下表(表中“元/吨·千米”表示每吨粮食运送1千米
所需人民币)拓展提升(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B
两库的总运费y(元)与x(吨)的函数关系式.
(1)y=12×20x+10×25(100-x)+1
2×15(70-x)+8×20[110-(100-x)]
=-30x+39 200,其中0≤x≤70;(2)当甲、乙两库各运往A、B两库多少吨粮食时,总
运费最省,最省的总运费是多少?
(2)上述一次函数中k=-30<0,所以y随x的增大而
减小,所以当x=70时,总运费最省,最省总运费
为-30×70+39 200=37 100(元).感谢聆听
6米,水位以每小时0.3米的速度匀速上升,则水库的水
位高度y米与时间x小时(0≤x≤5)的函数关系式为_______
________________.2y=6+0.3x课堂导案知识点:用一次函数解决生活中的方案选择问题【例题】某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2 090万元,但不超过2 096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如表:
(1)设A户型住房x套,总利润为y万元,求y与x的关系式.
(2)求x的范围;该公司有哪几种建房方案?
(3)该公司如何建房获得利润最大?课堂导案(3)y=-x+480,y随x的增大而减小,
当x最小时,y取最大值,
当x=48时,y最大=-48+480=432(万元),
答:公司建48套A户型,32套B户型房获得利润
最大,最大利润是432万元.课堂导案课堂导案【解析】(1)根据户A型的利润与B户型的利润和, 可得函数关系式;
(2)根据A户型B户型的投资不少于2 090万元,但不超过2 096万元,可得不等式组,根据解不等式组,可得方案;
(3)根据一次函数的增减性,可得答案.【点拔】本题考查了一次函数的应用,(1)A户型与B户型的利润和是解题关键;(2)解不等式组是解题关键;(3)k<0时,y随x的增大而减小是解题关键.课堂导案1.学校组织暑期夏令营,学校联系了报价均为每人
200元的两家旅行社,经协商,甲旅行社的优惠
条件是:全部师生7.5折优惠;乙旅行社的优惠条
件是:可免去一位老师的费用,其余师生8折优惠.
(1)分别写出两家旅行社所需的费用y(元)与师生人
数x(人)的函数关系式;对点训练(1)y甲=150x, y乙=160x-160课堂导案(2)学校应选择哪家旅行社?(2)当y甲>y乙时,150x>160x-160得x<16 ;
当y甲=y乙时,x=16;当y甲<y乙时,x>16.
所以当x>16时应选择甲旅行社,
当x<16时,应选择乙旅行社,
当x=16时两家旅行社一样.课堂导案2.实验学校计划组织共青团员372人到某爱国主义
基地接受教育,并安排8位老师同行,经学校与
汽车出租公司协商,有两种型号客车可供选择,
它们的载客量和租金如下表,
为了保证每人都有座位,学校决定租8辆车.课堂导案(1)写出符合要求的租车方案,并说明理由;
(1)设租甲种客车x辆,则50x+30(8-x)≥372+8
得x≥7又x≤8即7≤x≤8 ∴x=7或8,
所以有两种租车方案:
方案一:租甲种客车7辆,乙种客车1辆;
方案二:租甲种客车8辆,乙种客车0辆.课堂导案(2)设租甲种客车x辆,总租金共y(元),写出y与x
之间的函数关系式;
(2)y=400x+200(8-x)
即y=200x+1 600;
(3)在(1)方案中,求出租金最少的租车方案.
(3)当x=7时,y=3 000;当x=8时,y=3 200,
所以租金最少的方案是租甲种客车7辆,乙种客
车1辆.课后练案3.康乐公司在A、B两地分别有同型号的机器17台和
15台,现要运往甲地18台,乙地14台,从A、
B两地运往甲、乙两地的价格如下表:
(1)如果从A地运往甲地x台,求完成以上调运所需
总费用y(元)与x(台)的函数关系式;(1)y=600x+500(17-x)+400(18-x)+800(x-3)
=500x+13 300;课后练案(2)若康乐公司请你设计一种最佳调运方案,使总的费
用最少,该公司完成以上调运方案至少需要多少费
用?这什么?(2)由(1)知总运费y=500x+13 300,
∵x≥0,17-x≥0,18-x≥0,x-3≥0
∴3≤x≤17又∵k>0 ∴y随x的增大而增大,
∴当x=3时,y最小=500×3+13 300=14 800(元),
所以完成以上调运方案至少需用14 800元运费,
最佳方案是:由A调3台至甲地,14台至乙地;由B调
15台至甲地.拓展提升4.抗震救灾中,某县粮食局为了保证库存粮食的安全,
决定将甲、乙两个仓库的粮食,全部转移到具有较
强抗震功能的A、B两仓库.已知甲库有粮食100吨,
乙库有粮食80吨,而A库的容量为70吨,B库的容量
为110吨.从甲、乙两库到A、B两库的路程和运费
如下表(表中“元/吨·千米”表示每吨粮食运送1千米
所需人民币)拓展提升(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B
两库的总运费y(元)与x(吨)的函数关系式.
(1)y=12×20x+10×25(100-x)+1
2×15(70-x)+8×20[110-(100-x)]
=-30x+39 200,其中0≤x≤70;(2)当甲、乙两库各运往A、B两库多少吨粮食时,总
运费最省,最省的总运费是多少?
(2)上述一次函数中k=-30<0,所以y随x的增大而
减小,所以当x=70时,总运费最省,最省总运费
为-30×70+39 200=37 100(元).感谢聆听
