沪科版八上数学15.1轴对称图形-轴对称教学课件(34张)
文档属性
| 名称 | 沪科版八上数学15.1轴对称图形-轴对称教学课件(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览






文档简介
(共34张PPT)
第15章 轴对称图形与等腰三角形
第1节 轴对称图形
轴对称
课堂讲解
课时流程
1
2
轴对称
线段的垂直平分线
轴对称的性质
逐点
导讲练
课堂小结
课后
作业
1
知识点
轴对称
知1-讲
观察
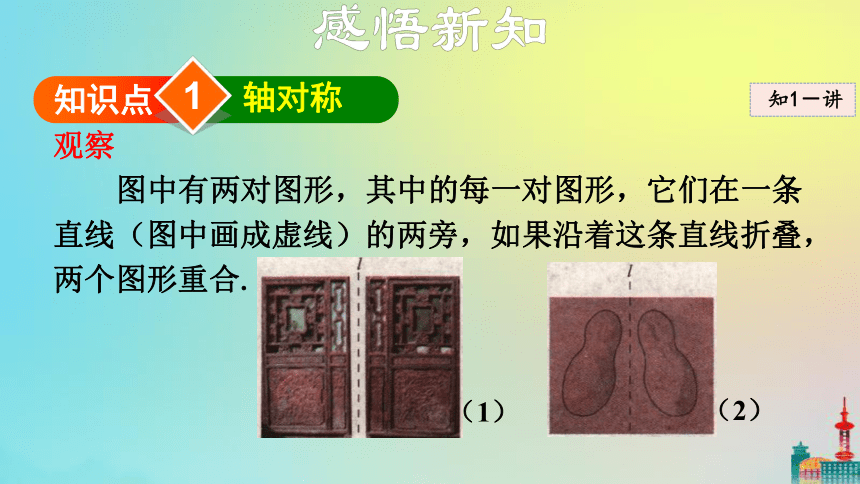
图中有两对图形,其中的每一对图形,它们在一条直线(图中画成虚线)的两旁,如果沿着这条直线折叠,两个图形重合.
(1)
(2)
知1-讲
1.轴对称的定义:平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点,也叫做对称点.
注意:不在对称轴上的对称点在对称轴的两侧,对称轴上的点的对称点是它本身.
知1-讲
2.轴对称的定义包含两层含义:(1)有两个图形,且形状、大小完全相同.(2)两个图形的位置必须满足沿一条直线折叠后能完全重合.
知1-讲
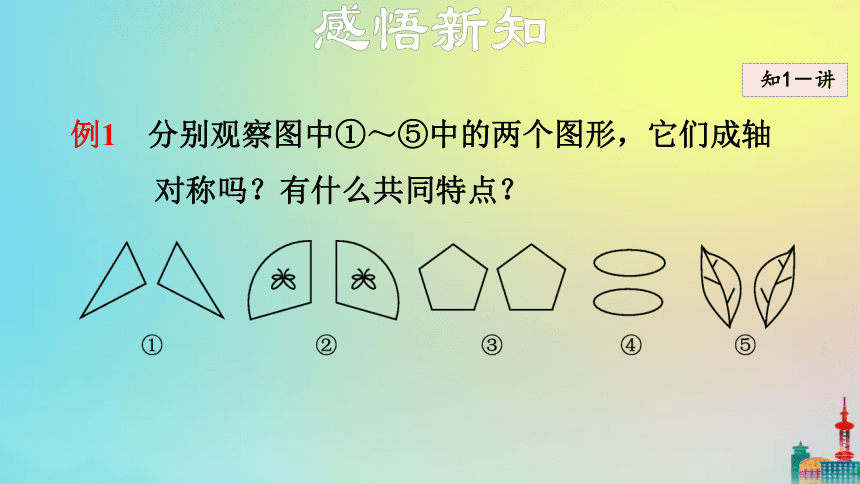
例1 分别观察图中①~⑤中的两个图形,它们成轴对称吗?有什么共同特点?
知1-讲
导引:尝试沿着一条直线折叠,观察两个图形是否能够完全重合,并根据轴对称的定义判断.
解:它们都成轴对称,每一组中都有两个图形,都可以沿某一条直线折叠使两个图形完全重合在一起,所以每组图中的两个图形成轴对称.
知1-讲
识别轴对称的方法:判断两个图形是否关于某条直线成轴对称,先观察两个图形的形状、大小,如果形状、大小相同,再看能否找到一条直线且将两个图形沿这条直线折叠,如果能够重合,则这两个图形成轴对称,否则不成轴对称.
知1-讲
轴对称图形与轴对称的区别与联系:
名称
关系 轴对称 轴对称图形
区别 对象不同 两个图形 一个图形
意义不同 两个图形的特殊位置关系 一个具有特殊形状的图形
对应点位置不同 对称点分别在两个图形上 对称点在同一个图形上
知1-讲
名称
关系 轴对称 轴对称图形
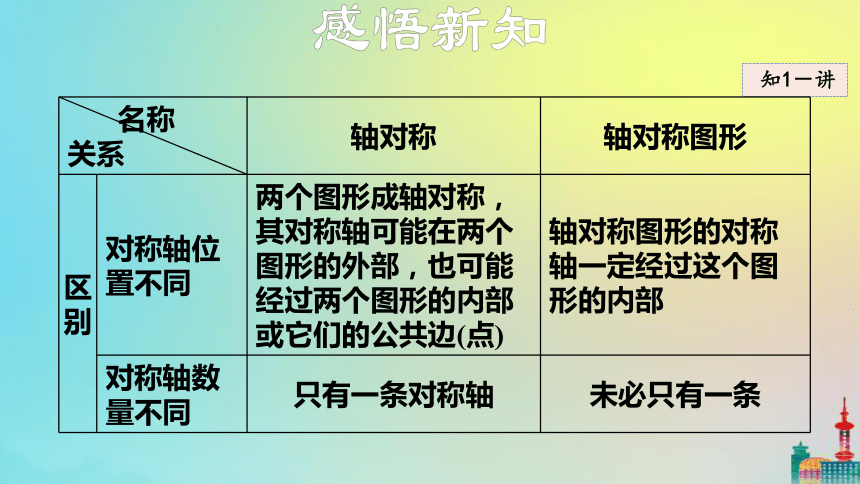
区别 对称轴位置不同 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 轴对称图形的对称轴一定经过这个图形的内部
对称轴数量不同 只有一条对称轴 未必只有一条
知1-讲
名称
关系 轴对称 轴对称图形
联系 (1)定义中都有一条直线,都要沿着这条直线折叠 (2)把成轴对称的两个图形看成一个整体,它就是一个轴对称图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线成轴对称
知1-讲
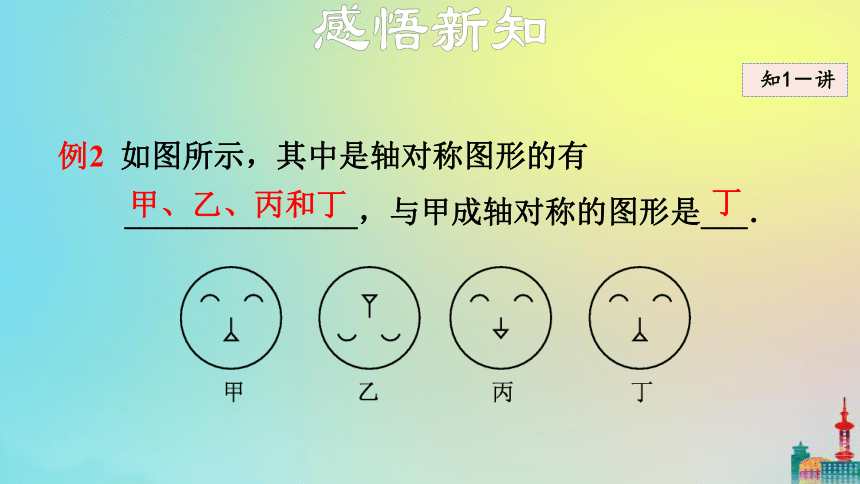
例2 如图所示,其中是轴对称图形的有 _______________,与甲成轴对称的图形是___.
甲、乙、丙和丁
丁
知1-讲
导引:根据轴对称和轴对称图形的定义,知甲、乙、丙、丁都是轴对称图形.沿某一条直线折叠后与甲能够完全重合的是丁.
知1-讲
判断轴对称图形和轴对称都需判断重合. 轴对称图形是指一个图形的特性,轴对称是指两个图形的位置关系,区别时要紧抓“一个图形还是两个图形”.
知1-练
C
1
如图,成轴对称的有( )个.
A.1 B.2 C.3 D.4
知1-练
A
2
下列说法中,正确的是( )
A.关于某条直线对称的两个三角形是全等三角形
B.全等的两个三角形是关于某条直线对称的
C.若两个图形关于某条直线对称,则这两个图形一 定分别位于这条直线的两侧
D.全等的两个图形一定成轴对称
2
知识点
线段的垂直平分线
知2-讲
思考
如图,△ABC与△A'B'C',关于直线l 对称,点A',B',C'分别是点A, B,C的对应点. 连接AA',设AA'与直线l交于点O1.
(1)直线l与线段AA'有怎样的位置关系?
(2)O1A与O1A'的长度有何关系?
知2-讲
线段的垂直平分线:
(1)定义:经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线.
要点精析:线段的垂直平分线必须满足两个条件:
①经过线段的中点;②垂直于这条线段.
(2)如图,CD是AB的垂直平分线?
知2-讲
例3 如图,直线AE是线段BC的垂直平分线,垂足为E.
求证:∠ABD=∠ACD.
导引:利用线段垂直平分线的定义结合
全等三角形知识证明.
知2-讲
证明:∵直线AE是线段BC的垂直平分线,
∴BE=CE,AE⊥BC,
∴∠AEB=∠AEC=90°.
在△BDE和△CDE中,∵
∴△BDE≌△CDE,∴∠DBE=∠DCE.
知2-讲
在△ABE和△ACE中,∵
∴△ABE≌△ACE,
∴∠ABE=∠ACE,
∴∠ABD=∠ACD.
知2-练
1 如图,已知△A′B′C′与△ABC关于直线MN对称,则MN垂直平分线段______________.
AA′BB′CC′
3
知识点
轴对称的性质
知3-讲
轴对称及轴对称图形的性质:
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
(2)轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(3)关于某一条直线成轴对称的两个图形是全等形.
知3-讲
轴对称的判定:
(1)如果两个图形的对应点所连线段被同一条直线垂直平分,那么这两个图形关于这条直线成轴对称.
(2)如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等,并且这两个图形成轴对称.
知3-讲
要点精析:无论是轴对称图形还是两个图形成轴对称都有一个共同特性:折叠后两部分(两个图形)能够完全重合;即两个图形成轴对称,其对应线段相等,对应角相等.
知3-讲
例6 如图是轴对称图形,图中直线l是它的对称轴.
(1)∠3和∠4有什么关系?AB与A′B′呢?
为什么?
(2)DD′与直线l有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
知3-讲
解:(1)∠3=∠4,AB=A′B′,因为轴对称图形中对应角相等,对应线段相等.
(2)直线l是DD′的垂直平分线,因为轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(3)AD=A′D′,∠1=∠2,DC=D′C′等.
知3-讲
要学会熟练应用轴对称图形的性质中的相等关系和垂直关系.要准确找出图中的对应点、对应角和对应线段.
知3-讲
例7 如图,△ABC是轴对称图形,且直线AD△ABC的对称轴,点E,F是线段AD上的任意两点,若△ABC的面积为12 cm2,则图中阴影部分的面积是____cm2.
6
知3-讲
导引:因为△ABC是轴对称图形,且直线AD是对称轴,所以△ABD与△ACD关于直线AD对称,所以 S△ABD=S△ACD= 又因为点E,F是AD上的任意两点,所以△BEF与△CEF关于直线AD对称, 所以S△CEF=S△BEF,所以阴影部分的面积S阴影=S△ABE+S△BEF+S△BDF=S△ABD= S△ABC=
知3-讲
如图,△ABC与△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.A、D的连线段被MN垂直平分
1
A
知3-讲
2
如图,△ABC和△AB′C′关于直线l对称,下列结论:①△ABC≌△AB′C′;②∠BAC′=∠B′AC;③直线l垂直平分线段CC′;④直线BC和B′C′的交点不一定在直线l上.其中正确的有( )
A.4个 B.3个
C.2个 D.1个
B
轴对称和轴对称图形的区别:
(1)定义不同;
(2)轴对称图形指的是一个图形,而两个图形成轴对称指的是两个图形;
(3)一个轴对称图形的对称轴可能有多条,而两个图形成轴对称的对称轴一般只有一条.
请完成对应习题。
第15章 轴对称图形与等腰三角形
第1节 轴对称图形
轴对称
课堂讲解
课时流程
1
2
轴对称
线段的垂直平分线
轴对称的性质
逐点
导讲练
课堂小结
课后
作业
1
知识点
轴对称
知1-讲
观察
图中有两对图形,其中的每一对图形,它们在一条直线(图中画成虚线)的两旁,如果沿着这条直线折叠,两个图形重合.
(1)
(2)
知1-讲
1.轴对称的定义:平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点,也叫做对称点.
注意:不在对称轴上的对称点在对称轴的两侧,对称轴上的点的对称点是它本身.
知1-讲
2.轴对称的定义包含两层含义:(1)有两个图形,且形状、大小完全相同.(2)两个图形的位置必须满足沿一条直线折叠后能完全重合.
知1-讲
例1 分别观察图中①~⑤中的两个图形,它们成轴对称吗?有什么共同特点?
知1-讲
导引:尝试沿着一条直线折叠,观察两个图形是否能够完全重合,并根据轴对称的定义判断.
解:它们都成轴对称,每一组中都有两个图形,都可以沿某一条直线折叠使两个图形完全重合在一起,所以每组图中的两个图形成轴对称.
知1-讲
识别轴对称的方法:判断两个图形是否关于某条直线成轴对称,先观察两个图形的形状、大小,如果形状、大小相同,再看能否找到一条直线且将两个图形沿这条直线折叠,如果能够重合,则这两个图形成轴对称,否则不成轴对称.
知1-讲
轴对称图形与轴对称的区别与联系:
名称
关系 轴对称 轴对称图形
区别 对象不同 两个图形 一个图形
意义不同 两个图形的特殊位置关系 一个具有特殊形状的图形
对应点位置不同 对称点分别在两个图形上 对称点在同一个图形上
知1-讲
名称
关系 轴对称 轴对称图形
区别 对称轴位置不同 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 轴对称图形的对称轴一定经过这个图形的内部
对称轴数量不同 只有一条对称轴 未必只有一条
知1-讲
名称
关系 轴对称 轴对称图形
联系 (1)定义中都有一条直线,都要沿着这条直线折叠 (2)把成轴对称的两个图形看成一个整体,它就是一个轴对称图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线成轴对称
知1-讲
例2 如图所示,其中是轴对称图形的有 _______________,与甲成轴对称的图形是___.
甲、乙、丙和丁
丁
知1-讲
导引:根据轴对称和轴对称图形的定义,知甲、乙、丙、丁都是轴对称图形.沿某一条直线折叠后与甲能够完全重合的是丁.
知1-讲
判断轴对称图形和轴对称都需判断重合. 轴对称图形是指一个图形的特性,轴对称是指两个图形的位置关系,区别时要紧抓“一个图形还是两个图形”.
知1-练
C
1
如图,成轴对称的有( )个.
A.1 B.2 C.3 D.4
知1-练
A
2
下列说法中,正确的是( )
A.关于某条直线对称的两个三角形是全等三角形
B.全等的两个三角形是关于某条直线对称的
C.若两个图形关于某条直线对称,则这两个图形一 定分别位于这条直线的两侧
D.全等的两个图形一定成轴对称
2
知识点
线段的垂直平分线
知2-讲
思考
如图,△ABC与△A'B'C',关于直线l 对称,点A',B',C'分别是点A, B,C的对应点. 连接AA',设AA'与直线l交于点O1.
(1)直线l与线段AA'有怎样的位置关系?
(2)O1A与O1A'的长度有何关系?
知2-讲
线段的垂直平分线:
(1)定义:经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线.
要点精析:线段的垂直平分线必须满足两个条件:
①经过线段的中点;②垂直于这条线段.
(2)如图,CD是AB的垂直平分线?
知2-讲
例3 如图,直线AE是线段BC的垂直平分线,垂足为E.
求证:∠ABD=∠ACD.
导引:利用线段垂直平分线的定义结合
全等三角形知识证明.
知2-讲
证明:∵直线AE是线段BC的垂直平分线,
∴BE=CE,AE⊥BC,
∴∠AEB=∠AEC=90°.
在△BDE和△CDE中,∵
∴△BDE≌△CDE,∴∠DBE=∠DCE.
知2-讲
在△ABE和△ACE中,∵
∴△ABE≌△ACE,
∴∠ABE=∠ACE,
∴∠ABD=∠ACD.
知2-练
1 如图,已知△A′B′C′与△ABC关于直线MN对称,则MN垂直平分线段______________.
AA′BB′CC′
3
知识点
轴对称的性质
知3-讲
轴对称及轴对称图形的性质:
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
(2)轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(3)关于某一条直线成轴对称的两个图形是全等形.
知3-讲
轴对称的判定:
(1)如果两个图形的对应点所连线段被同一条直线垂直平分,那么这两个图形关于这条直线成轴对称.
(2)如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等,并且这两个图形成轴对称.
知3-讲
要点精析:无论是轴对称图形还是两个图形成轴对称都有一个共同特性:折叠后两部分(两个图形)能够完全重合;即两个图形成轴对称,其对应线段相等,对应角相等.
知3-讲
例6 如图是轴对称图形,图中直线l是它的对称轴.
(1)∠3和∠4有什么关系?AB与A′B′呢?
为什么?
(2)DD′与直线l有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
知3-讲
解:(1)∠3=∠4,AB=A′B′,因为轴对称图形中对应角相等,对应线段相等.
(2)直线l是DD′的垂直平分线,因为轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(3)AD=A′D′,∠1=∠2,DC=D′C′等.
知3-讲
要学会熟练应用轴对称图形的性质中的相等关系和垂直关系.要准确找出图中的对应点、对应角和对应线段.
知3-讲
例7 如图,△ABC是轴对称图形,且直线AD△ABC的对称轴,点E,F是线段AD上的任意两点,若△ABC的面积为12 cm2,则图中阴影部分的面积是____cm2.
6
知3-讲
导引:因为△ABC是轴对称图形,且直线AD是对称轴,所以△ABD与△ACD关于直线AD对称,所以 S△ABD=S△ACD= 又因为点E,F是AD上的任意两点,所以△BEF与△CEF关于直线AD对称, 所以S△CEF=S△BEF,所以阴影部分的面积S阴影=S△ABE+S△BEF+S△BDF=S△ABD= S△ABC=
知3-讲
如图,△ABC与△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.A、D的连线段被MN垂直平分
1
A
知3-讲
2
如图,△ABC和△AB′C′关于直线l对称,下列结论:①△ABC≌△AB′C′;②∠BAC′=∠B′AC;③直线l垂直平分线段CC′;④直线BC和B′C′的交点不一定在直线l上.其中正确的有( )
A.4个 B.3个
C.2个 D.1个
B
轴对称和轴对称图形的区别:
(1)定义不同;
(2)轴对称图形指的是一个图形,而两个图形成轴对称指的是两个图形;
(3)一个轴对称图形的对称轴可能有多条,而两个图形成轴对称的对称轴一般只有一条.
请完成对应习题。
