沪科版八上数学15.2线段的垂直平分线教学课件(43张)
文档属性
| 名称 | 沪科版八上数学15.2线段的垂直平分线教学课件(43张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 08:42:08 | ||
图片预览









文档简介
(共43张PPT)
第15章 轴对称图形与等腰三角形
第2节 线段的垂直平分线
课堂讲解
课时流程
1
2
线段垂直平分线的画法
线段垂直平分线的性质
线段垂直平分线的判定
逐点
导讲练
课堂小结
课后
作业
1
知识点
线段垂直平分线的画法
知1-讲
怎样作出线段的垂直平分线?
问 题
知1-讲
通过折纸可以作出线段的垂直平分线.在半透明纸上画一条线段AA',折纸,使A与A'重合,得到的折痕l是线段 AA'的垂直平分线(如图).
步骤1
步骤2
步骤3
知1-讲
也可以用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
知1-讲
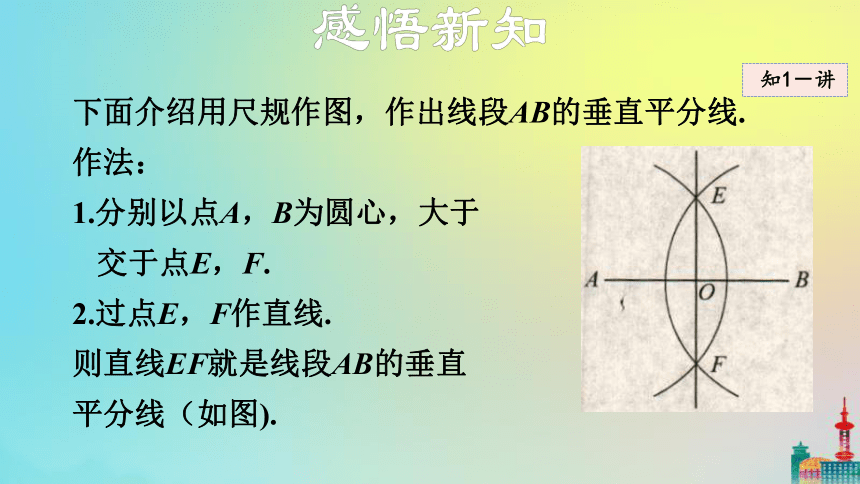
下面介绍用尺规作图,作出线段AB的垂直平分线.
作法:
1.分别以点A,B为圆心,大于
交于点E,F.
2.过点E,F作直线.
则直线EF就是线段AB的垂直
平分线(如图).
2
知识点
线段垂直平分线的性质
知2-讲
思考
为什么这样作出的直线EF,就是线段AB的垂直平分线呢?设所作直线EF交AB于点O,你能给出证明吗?
知2-讲
线段的垂直平分线的性质:
1.定理:线段垂直平分线上的点到线段两端的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端的距离相等.
表达方式:如图,l⊥AB,AO=BO,
点P在l上,则AP=BP.
2.作用:可用来证明两线段相等.
知2-讲
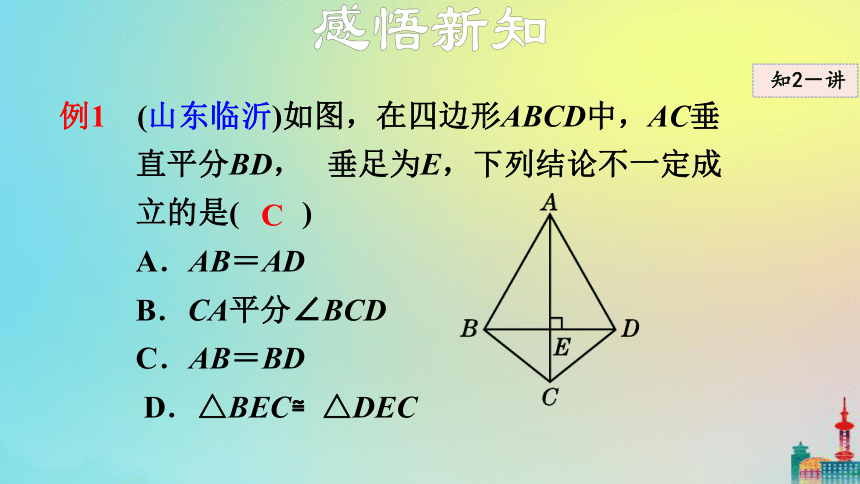
例1 (山东临沂)如图,在四边形ABCD中,AC垂直平分BD, 垂足为E,下列结论不一定成立的是( )
A.AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
C
知2-讲
导引:根据线段垂直平分线的性质得出AB与AD的关系,结合三角形全等对四个选项进行逐一验证.
∵AC垂直平分BD,∴AB=AD,BC=DC,
又∵AC=AC,∴△ABC≌△ADC,
∴∠BCA=∠DCA.
又∵BC=DC,CE=CE,
∴△BEC≌△DEC,∴选项A,B,D成立.
知2-讲
平面几何图形问题的解决方法:分析图形,结合已知条件对基本图形的形状进行判定是常用的方法,然后再根据具体图形的性质作出判断即可.
知2-讲
例2 如图,在△ABC中,AC=5,AB的垂直平分线DE交AB,AC于点E,D,
(1)若△BCD的周长为8,求BC的长;
(2) 若BC=4,求△BCD的周长.
知2-讲
导引:由DE是AB的垂直平分线,得AD=BD,所以BD与CD的长度和等于AC的长,所以由△BCD的周长可求BC的长,同样由BC的长也可求△BCD的周长.
知2-讲
解:∵DE是AB的垂直平分线,
∴AD=BD,∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.
知2-讲
本题运用了转化思想,用线段垂直平分线的性质把BD的长转化成AD的长,从而把未知的BD与CD的长度和转化成已知的线段AC的长.本题中AC的长、BC的长及△BCD的周长三者可互相转化,知其二可求第三者.
知2-讲
例3 如图,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD的度数是________.
10°
知2-讲
导引:在△ABC中,∵∠B=90°,∠A=40°,
∴∠ACB=50°.
∵MN是线段AC的垂直平分线,
∴DC=DA,AE=CE.又∵DE=DE,
∴△ADE≌△CDE(SSS),
∴∠DCE=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.
知2-讲
利用线段的垂直平分线的性质和定义得出边相等,从而得出三角形全等,再利用全等三角形中对应角相等确定∠DCA的度数,根据角度差解决问题.
知2-练
1
(中考·义乌)如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6 B.5 C.4 D.3
B
知2-练
(中考·临沂)如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD B.CA平分∠BCD
C.AB=BD D.△BEC≌△DEC
2
C
知2-练
3
(中考·遂宁)如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,若△BCN的周长是7 cm,则BC的长为( )
A.1 cm B.2 cm
C.3 cm D.4 cm
C
知2-练
(中考·荆州)如图,在△ABC中,AB=AC,
AB的垂直平分线交边AB于D点,交边AC于E
点,若△ABC与△EBC的周长分别是40 cm,
24 cm,则AB=________.
4
16cm
3
知识点
线段垂直平分线的判定
知3-讲
思考
你能写出上面定理的逆命题吗?它是真命题 吗?如果是真命题,请给出证明.
知3-讲
线段的垂直平分线的判定:
1.定理:到线段两端距离相等的点在线段的垂直平分线上.
(1)条件:点到线段两端距离相等;
结论:点在线段垂直平分线上.
(2)表达方式:如图,∵PA=PB,
∴点P在线段AB的垂直平分线上.
知3-讲
(3)作用:①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
2.拓展:三角形三边的垂直平分线交于一点,这点到三角形的三个顶点的距离相等,这个点叫这个三角形的外心.
知3-讲
例4 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.求证:直线AD是CE的垂直平分线.
导引:根据角平分线的定义可得
∠BAD=∠CAD,结合已知条件可证△ADE≌△ADC,所以DE=DC,AE=AC,所以点D、A都在CE的垂直平分线上,从而就能证明结论.
知3-讲
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠ACB=90°,DE⊥AB,
∴∠AED=∠ACB=90°.
又∵AD=AD,
∴△ADE≌△ADC,∴CD=DE,AC=AE,
∴点D、A都在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.
知3-讲
利用判定定理证一条直线是线段的垂直平分线,必须证明这条直线上有两点到线段两端的距离相等(即证有两点在线段的垂直平分线上).易错之处:只证明一个点在线段的垂直平分线上,就说过该点的直线是线段的垂直平分线.因为过该点的直线有无穷多条,其中只有一条是线段的垂直平分线.注意:证线段的垂直平分线也可以利用定义.
知3-讲
例5 已知:如图,△ABC的边AB, AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
知3-讲
证明:连接PA,PB,PC.
∵点P在AB, AC的垂直平分线上,(已知)
∴PA = PB, PA = PC.(线段垂直平分线
上的点到线段两端的距离相等)
∴PB = PC.(等量代换)
∴点P在BC的垂直平分线上.(到线段两端距离相等的点在线段的垂直平分线上)
知3-讲
例6 如图,已知AB=AD,BC=DC,E是AC上一点,求证:
(1)BE=DE;
(2)∠ABE=∠ADE.
知3-讲
导引:(1)连接BD,要证BE=DE,只要证明E点是线段BD的垂直平分线上的点即可.由AB=AD,说明A点是线段BD的垂直平分线上的点,由BC=DC,说明C点也是线段BD的垂直平分线上的点,所以AC是线段BD的垂直平分线,而已知E是AC上一点,问题得以解决.(2)要证明角相等,只需证明△ABE≌△ADE即可.
知3-讲
证明:(1)连接BD,如图,
∵AB=AD,BC=CD,
∴A,C两点均在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
又∵E是AC上一点,
∴BE=DE.
知3-讲
证明: (2)在△ABE和△ADE中,
∵AB=AD,BE=DE,AE=AE,
∴△ABE≌△ADE(SSS),
∴∠ABE=∠ADE.
知3-讲
由线段的垂直平分线的判定定理确定AC是线段BD的垂直平分线,再由线段垂直平分线的性质得BE=DE,这是线段垂直平分线的性质和判定定理的综合运用.
知3-讲
例7 如图,某城市规划局为了方便居民的生活,计划在三个住宅小区A,B,C之间修建一个购物中心,试问:该购物中心
应建于何处,才能使得它到
三个小区的距离相等?
知3-讲
导引:本题转化为数学问题就是要找一个点,使它到三角形的三个顶点的距离相等.首先考虑到A,B两点距离相等的点应该在线段AB的垂直平分线上,到B,C两点距离相等的点应该在线段BC的垂直平分线上,两条垂直平分线的交点即为所求的点.
知3-讲
解:连接AB,BC,分别作AB,BC的垂直平分线DE,GF,两直线交于点M,则点M就是所要确定的购物中心的位置.如图.
知3-讲
解决作图选点性问题:若要找到某两个点的距离相等的点,一般在这两点所连线段的垂直平分线上去找.
知3-练
锐角三角形ABC内有一点P,满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
1
D
知3-练
如图,点D在三角形ABC的BC边上,且BC=BD+AD,则点D在线段( )的垂直平分线上.
A.AB B.AC
C.BC D.不确定
2
B
1.线段的垂直平分线的性质和判定的“两点作用”:
(1)利用线段垂直平分线的性质可证明两线段相等,只需直线满足垂直、平分即可;
(2)利用线段垂直平分线的判定可证明垂直关系和线段的相等关系.
2.应用线段垂直平分线的性质要注意两点:(1)点一定在垂直平分线上;(2)距离指的是点到线段两个端点的距离.
请完成对应习题。
第15章 轴对称图形与等腰三角形
第2节 线段的垂直平分线
课堂讲解
课时流程
1
2
线段垂直平分线的画法
线段垂直平分线的性质
线段垂直平分线的判定
逐点
导讲练
课堂小结
课后
作业
1
知识点
线段垂直平分线的画法
知1-讲
怎样作出线段的垂直平分线?
问 题
知1-讲
通过折纸可以作出线段的垂直平分线.在半透明纸上画一条线段AA',折纸,使A与A'重合,得到的折痕l是线段 AA'的垂直平分线(如图).
步骤1
步骤2
步骤3
知1-讲
也可以用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
知1-讲
下面介绍用尺规作图,作出线段AB的垂直平分线.
作法:
1.分别以点A,B为圆心,大于
交于点E,F.
2.过点E,F作直线.
则直线EF就是线段AB的垂直
平分线(如图).
2
知识点
线段垂直平分线的性质
知2-讲
思考
为什么这样作出的直线EF,就是线段AB的垂直平分线呢?设所作直线EF交AB于点O,你能给出证明吗?
知2-讲
线段的垂直平分线的性质:
1.定理:线段垂直平分线上的点到线段两端的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端的距离相等.
表达方式:如图,l⊥AB,AO=BO,
点P在l上,则AP=BP.
2.作用:可用来证明两线段相等.
知2-讲
例1 (山东临沂)如图,在四边形ABCD中,AC垂直平分BD, 垂足为E,下列结论不一定成立的是( )
A.AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
C
知2-讲
导引:根据线段垂直平分线的性质得出AB与AD的关系,结合三角形全等对四个选项进行逐一验证.
∵AC垂直平分BD,∴AB=AD,BC=DC,
又∵AC=AC,∴△ABC≌△ADC,
∴∠BCA=∠DCA.
又∵BC=DC,CE=CE,
∴△BEC≌△DEC,∴选项A,B,D成立.
知2-讲
平面几何图形问题的解决方法:分析图形,结合已知条件对基本图形的形状进行判定是常用的方法,然后再根据具体图形的性质作出判断即可.
知2-讲
例2 如图,在△ABC中,AC=5,AB的垂直平分线DE交AB,AC于点E,D,
(1)若△BCD的周长为8,求BC的长;
(2) 若BC=4,求△BCD的周长.
知2-讲
导引:由DE是AB的垂直平分线,得AD=BD,所以BD与CD的长度和等于AC的长,所以由△BCD的周长可求BC的长,同样由BC的长也可求△BCD的周长.
知2-讲
解:∵DE是AB的垂直平分线,
∴AD=BD,∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.
知2-讲
本题运用了转化思想,用线段垂直平分线的性质把BD的长转化成AD的长,从而把未知的BD与CD的长度和转化成已知的线段AC的长.本题中AC的长、BC的长及△BCD的周长三者可互相转化,知其二可求第三者.
知2-讲
例3 如图,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD的度数是________.
10°
知2-讲
导引:在△ABC中,∵∠B=90°,∠A=40°,
∴∠ACB=50°.
∵MN是线段AC的垂直平分线,
∴DC=DA,AE=CE.又∵DE=DE,
∴△ADE≌△CDE(SSS),
∴∠DCE=∠A=40°.
∴∠BCD=∠ACB-∠DCA=50°-40°=10°.
知2-讲
利用线段的垂直平分线的性质和定义得出边相等,从而得出三角形全等,再利用全等三角形中对应角相等确定∠DCA的度数,根据角度差解决问题.
知2-练
1
(中考·义乌)如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6 B.5 C.4 D.3
B
知2-练
(中考·临沂)如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD B.CA平分∠BCD
C.AB=BD D.△BEC≌△DEC
2
C
知2-练
3
(中考·遂宁)如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,若△BCN的周长是7 cm,则BC的长为( )
A.1 cm B.2 cm
C.3 cm D.4 cm
C
知2-练
(中考·荆州)如图,在△ABC中,AB=AC,
AB的垂直平分线交边AB于D点,交边AC于E
点,若△ABC与△EBC的周长分别是40 cm,
24 cm,则AB=________.
4
16cm
3
知识点
线段垂直平分线的判定
知3-讲
思考
你能写出上面定理的逆命题吗?它是真命题 吗?如果是真命题,请给出证明.
知3-讲
线段的垂直平分线的判定:
1.定理:到线段两端距离相等的点在线段的垂直平分线上.
(1)条件:点到线段两端距离相等;
结论:点在线段垂直平分线上.
(2)表达方式:如图,∵PA=PB,
∴点P在线段AB的垂直平分线上.
知3-讲
(3)作用:①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
2.拓展:三角形三边的垂直平分线交于一点,这点到三角形的三个顶点的距离相等,这个点叫这个三角形的外心.
知3-讲
例4 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.求证:直线AD是CE的垂直平分线.
导引:根据角平分线的定义可得
∠BAD=∠CAD,结合已知条件可证△ADE≌△ADC,所以DE=DC,AE=AC,所以点D、A都在CE的垂直平分线上,从而就能证明结论.
知3-讲
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠ACB=90°,DE⊥AB,
∴∠AED=∠ACB=90°.
又∵AD=AD,
∴△ADE≌△ADC,∴CD=DE,AC=AE,
∴点D、A都在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.
知3-讲
利用判定定理证一条直线是线段的垂直平分线,必须证明这条直线上有两点到线段两端的距离相等(即证有两点在线段的垂直平分线上).易错之处:只证明一个点在线段的垂直平分线上,就说过该点的直线是线段的垂直平分线.因为过该点的直线有无穷多条,其中只有一条是线段的垂直平分线.注意:证线段的垂直平分线也可以利用定义.
知3-讲
例5 已知:如图,△ABC的边AB, AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
知3-讲
证明:连接PA,PB,PC.
∵点P在AB, AC的垂直平分线上,(已知)
∴PA = PB, PA = PC.(线段垂直平分线
上的点到线段两端的距离相等)
∴PB = PC.(等量代换)
∴点P在BC的垂直平分线上.(到线段两端距离相等的点在线段的垂直平分线上)
知3-讲
例6 如图,已知AB=AD,BC=DC,E是AC上一点,求证:
(1)BE=DE;
(2)∠ABE=∠ADE.
知3-讲
导引:(1)连接BD,要证BE=DE,只要证明E点是线段BD的垂直平分线上的点即可.由AB=AD,说明A点是线段BD的垂直平分线上的点,由BC=DC,说明C点也是线段BD的垂直平分线上的点,所以AC是线段BD的垂直平分线,而已知E是AC上一点,问题得以解决.(2)要证明角相等,只需证明△ABE≌△ADE即可.
知3-讲
证明:(1)连接BD,如图,
∵AB=AD,BC=CD,
∴A,C两点均在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
又∵E是AC上一点,
∴BE=DE.
知3-讲
证明: (2)在△ABE和△ADE中,
∵AB=AD,BE=DE,AE=AE,
∴△ABE≌△ADE(SSS),
∴∠ABE=∠ADE.
知3-讲
由线段的垂直平分线的判定定理确定AC是线段BD的垂直平分线,再由线段垂直平分线的性质得BE=DE,这是线段垂直平分线的性质和判定定理的综合运用.
知3-讲
例7 如图,某城市规划局为了方便居民的生活,计划在三个住宅小区A,B,C之间修建一个购物中心,试问:该购物中心
应建于何处,才能使得它到
三个小区的距离相等?
知3-讲
导引:本题转化为数学问题就是要找一个点,使它到三角形的三个顶点的距离相等.首先考虑到A,B两点距离相等的点应该在线段AB的垂直平分线上,到B,C两点距离相等的点应该在线段BC的垂直平分线上,两条垂直平分线的交点即为所求的点.
知3-讲
解:连接AB,BC,分别作AB,BC的垂直平分线DE,GF,两直线交于点M,则点M就是所要确定的购物中心的位置.如图.
知3-讲
解决作图选点性问题:若要找到某两个点的距离相等的点,一般在这两点所连线段的垂直平分线上去找.
知3-练
锐角三角形ABC内有一点P,满足PA=PB=PC,则点P是△ABC( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
1
D
知3-练
如图,点D在三角形ABC的BC边上,且BC=BD+AD,则点D在线段( )的垂直平分线上.
A.AB B.AC
C.BC D.不确定
2
B
1.线段的垂直平分线的性质和判定的“两点作用”:
(1)利用线段垂直平分线的性质可证明两线段相等,只需直线满足垂直、平分即可;
(2)利用线段垂直平分线的判定可证明垂直关系和线段的相等关系.
2.应用线段垂直平分线的性质要注意两点:(1)点一定在垂直平分线上;(2)距离指的是点到线段两个端点的距离.
请完成对应习题。
