沪科版八上数学15.3 等腰三角形-- 等腰三角形的判定教学课件(27张)
文档属性
| 名称 | 沪科版八上数学15.3 等腰三角形-- 等腰三角形的判定教学课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 08:46:18 | ||
图片预览







文档简介
(共27张PPT)
第15章 轴对称图形与等腰三角形
第3节 等腰三角形
等腰三角形的判定
课堂讲解
课时流程
1
2
等腰三角形的判定
等边三角形的判定
逐点
导讲练
课堂小结
课后
作业
1
知识点
等腰三角形的判定
知1-讲
思考
“等腰三角形两个底角相等”的逆命题
是真命题吗?请与你的同学研究讨论后
作出判断.
知1-讲
1.定理:有两个角相等的三角形是等腰三角形.
(简称“等角对等边”)
应用格式:在△ABC中,∵∠B=∠C,
∴AB=AC.
知1-讲
2.等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:等边 等角.
知1-讲
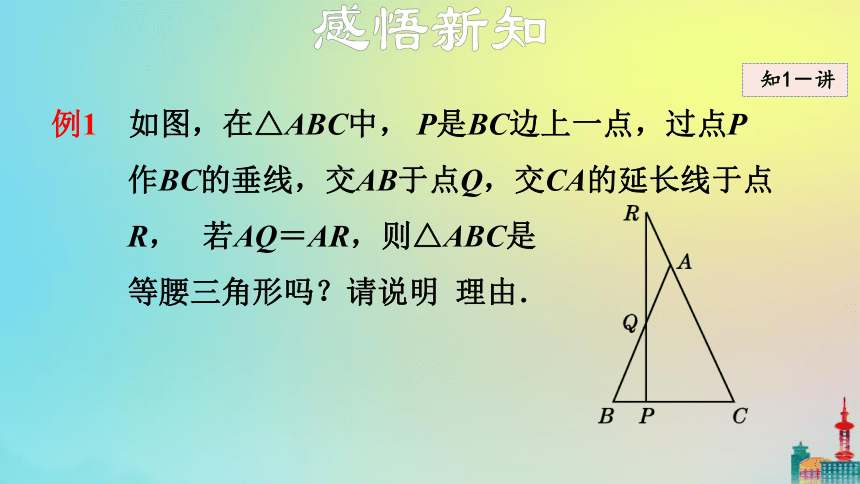
例1 如图,在△ABC中, P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R, 若AQ=AR,则△ABC是
等腰三角形吗?请说明 理由.
知1-讲
导引:要说明△ABC为等腰三角形,由图可知只要说明∠B=∠C即可,而∠B,∠C分别在两个直角三角形中,因此只要说明∠B,∠C的余角∠BQP, ∠R相等即可.
知1-讲
解:△ABC是等腰三角形.理由如下:
∵AQ=AR,∴∠R=∠AQR.
又∵∠BQP=∠AQR,∴∠R=∠BQP.
在Rt△QPB和Rt△RPC中,
∠B+∠BQP=90°,∠C+∠R=90°,
∴∠B=∠C, ∴AB=AC.
知1-讲
本题运用了转化思想,将要说明的两相等角利用等角的余角相等转化为说明其余角相等;对顶角这一隐含条件在推导角的相等关系中起了关键的桥梁作用.
知1-讲
例2 如图,在△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点 D,E.求证:DE=BD+AE.
知1-讲
导引:要证DE=BD+AE,而由图知DE=DP+PE.因此只需证BD+AE=DP+PE即可.即需证BD=DP, AE=PE,而要证这两组边相等,只需证明它们所对的角相等,因此我们可以把证角相等作为切入口 进行证明.
知1-讲
证明:∵DE∥AB,
∴∠ABP=∠DPB, ∠BAP=∠EPA.
∵∠ABC,∠CAB的平分线交于点P,
∴∠ABP=∠DBP, ∠BAP=∠EAP,
∴∠DBP=∠DPB, ∠EAP=∠EPA,
∴DP=DB,EP=AE,
∴DP+EP=DB+AE,即DE=BD+AE.
知1-讲
(1)本题运用平行线性质以及角平分线的定义证明角之间的相等关系,进而运用等腰三角形的判定得出线段之间的长度关系,这是证几何题常用的方法.
知1-讲
(2)如图中角的一边与角的平分线及角另一边的平行线所构成的三角形是等腰三角形,这是一个基本的图形,在以后学习平行四边形时会经常遇到.
知1-练
1
在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70°
B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90°
D.∠A=80°,∠B=60°
B
知1-练
2
如图,在△ABC中,AB=AC,BD是AC边上 的高,CE是AB边上的高,它们相交于点O,则图中除△ABC外一定是等腰三角形的是( )
A.△ABD B.△ACE
C.△OBC D.△OCD
C
2
知识点
等边三角形的判定
知2-讲
等边三角形的判定
1.推论1:三个角都相等的三角形是等边三角形;
推论2:有一个角是60°的等腰三角形是等边三角形.
2.注意事项:推论1在任意三角形中都适用,推论2的
前提条件是等腰三角形.因此要结合题目的条件选
择适当的方法.
知2-讲
如图,在等边三角形ABC中,∠ABC和∠ACB的平分线相交于点O,OB,OC的垂直平分线分别交BC于点E,F,连接OE,OF.
求证:△OEF是等边三角形.
例3
导引:
从题中条件看,利用三角形
的外角性质易求得∠OEF=∠OFE=60°,
从而证明△OEF是等边三角形.
知2-讲
证明:∵E,F分别是线段OB,OC的垂直平分线上的点,
∴OE=BE,OF=CF,
∴∠OBE=∠BOE,∠OCF=∠COF.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
知2-讲
证明:又∵BO,CO分别平分∠ABC和∠ACB,
∴∠OBE=∠BOE=∠OCF=∠COF=30°.
∴∠OEF=∠OFE=60°.
∴∠EOF=180°-2×60°=60°.
∴△OEF是等边三角形.
知2-讲
证明一个三角形是等边三角形,要根据已知条件选择适当的方法.(1)如果已知三边关系,则选用等边三角形定义来判定.(2)若已知三角关系,则选用“三个角都相等的三角形是等边三角形”来判定.(3)若已知是等腰三角形,则选用“有一个角是60°的等腰三角形是等边三角形”来判定.
知2-讲
例5 如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC,证明:△ADE是等边三角形.
导引:从题中条件看用“HL”证明Rt△ABD≌Rt△ACE,可得
AD=AE,∠BAD=∠CAE=60°,因此用推论2证△ADE是等边三角形.
知2-讲
证明:∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=60°,BD⊥AC.
∵AE⊥EC,∴∠BDA=∠CEA=90°.
在Rt△ABD和Rt△ACE中,
∴Rt△ABD≌Rt△ACE,
∴AD=AE,∠EAD=∠BAD=60°,
∴△ADE是等边三角形.
知2-练
1
如图,△ABC是等边三角形,D,E,F为各边中点,则图中共有等边三角形( )
A.2个 B.3个 C.4个 D.5个
D
等腰三角形的三种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相等的三角形是等腰三角形”来证明.
(2)当三角形中有两个角相等时,应用“有两个角相等的三角形是等腰三角形”来证明.
(3)当线段垂直平分线上的点与线段两端点构成三角形时,应用“线段垂直平分线上的点到线段两端的距离相等”来证明.
根据条件判定等边三角形的解题技巧:
(1)若已知三边关系,则考虑用“三条边都相等的三角形是等边三角形”判定.
(2)若已知三角关系,则根据“三个角都相等的三角形是等边三角形”判定.
(3)若已知三角形是等腰三角形,则根据“有一个角是60°的等腰三角形是等边三角形”判定.
请完成对应习题。
第15章 轴对称图形与等腰三角形
第3节 等腰三角形
等腰三角形的判定
课堂讲解
课时流程
1
2
等腰三角形的判定
等边三角形的判定
逐点
导讲练
课堂小结
课后
作业
1
知识点
等腰三角形的判定
知1-讲
思考
“等腰三角形两个底角相等”的逆命题
是真命题吗?请与你的同学研究讨论后
作出判断.
知1-讲
1.定理:有两个角相等的三角形是等腰三角形.
(简称“等角对等边”)
应用格式:在△ABC中,∵∠B=∠C,
∴AB=AC.
知1-讲
2.等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:等边 等角.
知1-讲
例1 如图,在△ABC中, P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R, 若AQ=AR,则△ABC是
等腰三角形吗?请说明 理由.
知1-讲
导引:要说明△ABC为等腰三角形,由图可知只要说明∠B=∠C即可,而∠B,∠C分别在两个直角三角形中,因此只要说明∠B,∠C的余角∠BQP, ∠R相等即可.
知1-讲
解:△ABC是等腰三角形.理由如下:
∵AQ=AR,∴∠R=∠AQR.
又∵∠BQP=∠AQR,∴∠R=∠BQP.
在Rt△QPB和Rt△RPC中,
∠B+∠BQP=90°,∠C+∠R=90°,
∴∠B=∠C, ∴AB=AC.
知1-讲
本题运用了转化思想,将要说明的两相等角利用等角的余角相等转化为说明其余角相等;对顶角这一隐含条件在推导角的相等关系中起了关键的桥梁作用.
知1-讲
例2 如图,在△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点 D,E.求证:DE=BD+AE.
知1-讲
导引:要证DE=BD+AE,而由图知DE=DP+PE.因此只需证BD+AE=DP+PE即可.即需证BD=DP, AE=PE,而要证这两组边相等,只需证明它们所对的角相等,因此我们可以把证角相等作为切入口 进行证明.
知1-讲
证明:∵DE∥AB,
∴∠ABP=∠DPB, ∠BAP=∠EPA.
∵∠ABC,∠CAB的平分线交于点P,
∴∠ABP=∠DBP, ∠BAP=∠EAP,
∴∠DBP=∠DPB, ∠EAP=∠EPA,
∴DP=DB,EP=AE,
∴DP+EP=DB+AE,即DE=BD+AE.
知1-讲
(1)本题运用平行线性质以及角平分线的定义证明角之间的相等关系,进而运用等腰三角形的判定得出线段之间的长度关系,这是证几何题常用的方法.
知1-讲
(2)如图中角的一边与角的平分线及角另一边的平行线所构成的三角形是等腰三角形,这是一个基本的图形,在以后学习平行四边形时会经常遇到.
知1-练
1
在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70°
B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90°
D.∠A=80°,∠B=60°
B
知1-练
2
如图,在△ABC中,AB=AC,BD是AC边上 的高,CE是AB边上的高,它们相交于点O,则图中除△ABC外一定是等腰三角形的是( )
A.△ABD B.△ACE
C.△OBC D.△OCD
C
2
知识点
等边三角形的判定
知2-讲
等边三角形的判定
1.推论1:三个角都相等的三角形是等边三角形;
推论2:有一个角是60°的等腰三角形是等边三角形.
2.注意事项:推论1在任意三角形中都适用,推论2的
前提条件是等腰三角形.因此要结合题目的条件选
择适当的方法.
知2-讲
如图,在等边三角形ABC中,∠ABC和∠ACB的平分线相交于点O,OB,OC的垂直平分线分别交BC于点E,F,连接OE,OF.
求证:△OEF是等边三角形.
例3
导引:
从题中条件看,利用三角形
的外角性质易求得∠OEF=∠OFE=60°,
从而证明△OEF是等边三角形.
知2-讲
证明:∵E,F分别是线段OB,OC的垂直平分线上的点,
∴OE=BE,OF=CF,
∴∠OBE=∠BOE,∠OCF=∠COF.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
知2-讲
证明:又∵BO,CO分别平分∠ABC和∠ACB,
∴∠OBE=∠BOE=∠OCF=∠COF=30°.
∴∠OEF=∠OFE=60°.
∴∠EOF=180°-2×60°=60°.
∴△OEF是等边三角形.
知2-讲
证明一个三角形是等边三角形,要根据已知条件选择适当的方法.(1)如果已知三边关系,则选用等边三角形定义来判定.(2)若已知三角关系,则选用“三个角都相等的三角形是等边三角形”来判定.(3)若已知是等腰三角形,则选用“有一个角是60°的等腰三角形是等边三角形”来判定.
知2-讲
例5 如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC,证明:△ADE是等边三角形.
导引:从题中条件看用“HL”证明Rt△ABD≌Rt△ACE,可得
AD=AE,∠BAD=∠CAE=60°,因此用推论2证△ADE是等边三角形.
知2-讲
证明:∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=60°,BD⊥AC.
∵AE⊥EC,∴∠BDA=∠CEA=90°.
在Rt△ABD和Rt△ACE中,
∴Rt△ABD≌Rt△ACE,
∴AD=AE,∠EAD=∠BAD=60°,
∴△ADE是等边三角形.
知2-练
1
如图,△ABC是等边三角形,D,E,F为各边中点,则图中共有等边三角形( )
A.2个 B.3个 C.4个 D.5个
D
等腰三角形的三种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相等的三角形是等腰三角形”来证明.
(2)当三角形中有两个角相等时,应用“有两个角相等的三角形是等腰三角形”来证明.
(3)当线段垂直平分线上的点与线段两端点构成三角形时,应用“线段垂直平分线上的点到线段两端的距离相等”来证明.
根据条件判定等边三角形的解题技巧:
(1)若已知三边关系,则考虑用“三条边都相等的三角形是等边三角形”判定.
(2)若已知三角关系,则根据“三个角都相等的三角形是等边三角形”判定.
(3)若已知三角形是等腰三角形,则根据“有一个角是60°的等腰三角形是等边三角形”判定.
请完成对应习题。
