沪科版八上数学15.3 等腰三角形--等腰三角形的性质教学课件(55张)
文档属性
| 名称 | 沪科版八上数学15.3 等腰三角形--等腰三角形的性质教学课件(55张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览









文档简介
(共55张PPT)
第15章 轴对称图形与等腰三角形
第3节 等腰三角形
等腰三角形的性质
课堂讲解
课时流程
1
2
等腰三角形的轴对称性、三线合一
等腰三角形的边角性质:等边对等角
等边三角形的性质:每个角都等于60°
逐点
导讲练
课堂小结
课后
作业
等腰三角形是一类特殊的三角形.等腰三角形除具有一般三角形的性质外,还具有什么样的特殊性质呢?
1
知识点
等腰三角形的轴对称性、三线合一
知1-讲
等腰三角形的轴对称性:“三线合一”
定理1:等腰三角形顶角的平分线垂直平分底边.
结论:等腰三角形顶角的平分线、底边上的中线、底边上的高相 互重合(简称“三线合一”).
知1-讲
要点精析:
(1)含义:这是等腰三角形所特有的性质,它实际是一组定理,应用过程中,在三角形是等腰三角形前提下,“顶角的平分线、底边上的中线、底边上的高”只要知道其中“一线”,就可以说明是其他“两线”.
知1-讲
(3)对称性:等腰三角形是轴对称图形,顶角平分线(或底边上的高、底边上的中线)所在的直线是它的对称轴.
(2)作用:是证明线段相等、角相等、垂直等关系的重要方法,应用广泛.
知1-讲
(4)应用格式:如图,在△ABC中,
①∵AB=AC,AD⊥BC,∴AD平分
∠BAC(或BD=CD);
②∵AB=AC,BD=DC,∴AD⊥BC(或AD平分∠BAC);
③∵AB=AC,AD平分∠BAC,∴BD=DC(或AD⊥BC).
知1-讲
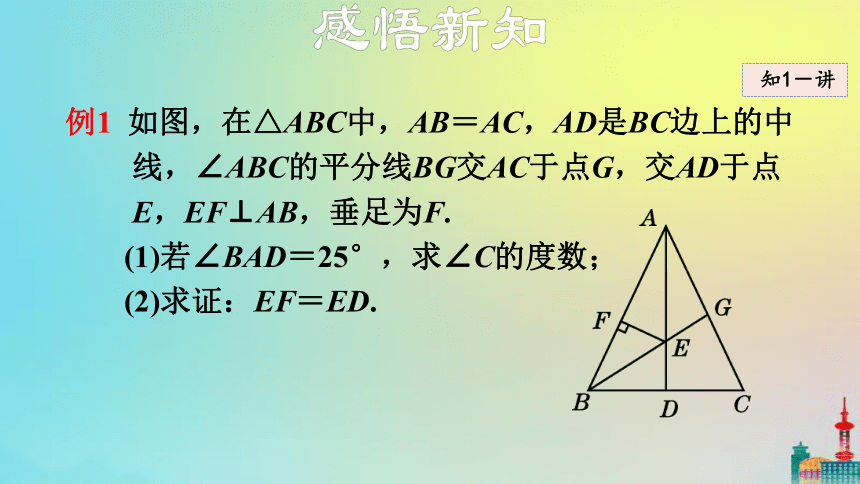
例1 如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
知1-讲
解: (1) ∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,
∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴ ∠C=∠ABC=
知1-讲
证明: (2) ∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∴∠BDE=90°.
∵EF⊥AB,
∴∠BFE=90°,∴∠BFE=∠BDE.
又∵BG平分∠ABC,∴∠FBE=∠DBE.
∵BE为公共边,
∴△BDE≌△BFE,∴EF=ED.
知1-讲
等腰三角形“三线合一”的性质是证明角相等、线段相等和垂直关系的既重要又简便的方法;因为题目的证明或计算所求结果大多都是单一的,所以“三线合一”的性质的应用也是单一的,一般得出一个结论,因此应用要灵活.在等腰三角形中,作“三线”中“一线”,利用“三线合一”是等腰三角形中常用的方法.
知1-讲
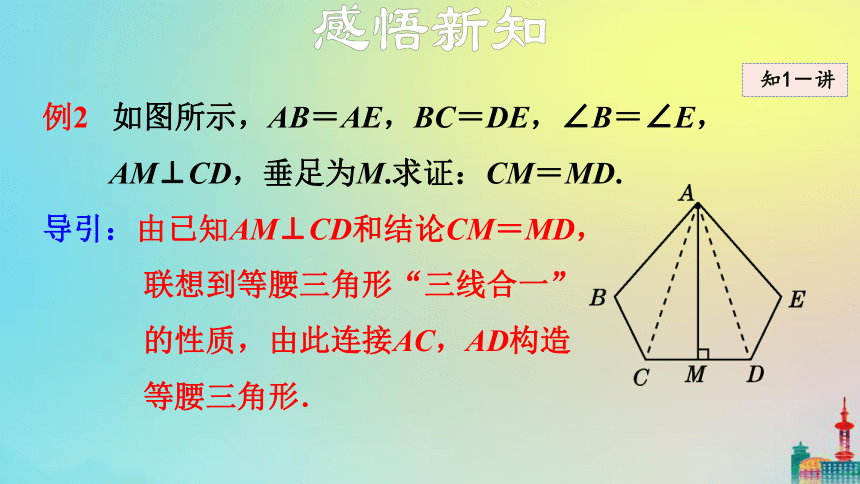
例2 如图所示,AB=AE,BC=DE,∠B=∠E, AM⊥CD,垂足为M.求证:CM=MD.
导引:由已知AM⊥CD和结论CM=MD,
联想到等腰三角形“三线合一”
的性质,由此连接AC,AD构造
等腰三角形.
知1-讲
证明:如图,连接AC,AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).∴AC=AD.
又∵AM⊥CD,∴CM=MD.
知1-讲
对于单一等腰三角形构造“三线合一”的基本图形,作底边上的高、中线还是顶角平分线,可根据解题需要作辅助线;对于叠合等腰三角形构造“三线合一”的基本图形,则需巧作辅助线,下面就如下几种图形说明巧作辅助线的方法:
知1-讲
知1-讲
1.如图甲的情形,需作底边上的高;
2.如图乙的情形,需作顶角平分线;
3.如图丙的情形,需作中线;
4.如图丁的情形,需连接AD并延长再证其是“三线”即可.
知1-练
1
如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;②DE=DF;③BD=CD;④若点P在直线AD上,则PB=PC.
其中正确的是( )
A.① B.①②
C.①②③ D.①②③④
D
2
知识点
等腰三角形的边角性质:等边对等角
知2-讲
操作
画一个等腰三角形ABC,如图(1).把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.
知2-讲
操作
如图(2).观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?
AD与BC垂直吗?为什么?
等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴.
知2-讲
等腰三角形的边角性质:等边对等角
定理1:等腰三角形的两底角相等(简称“等边对等角”).
要点精析:
(1)适用条件:必须在同一个三角形中.
(2)应用格式:在△ABC中,因为AB=AC,所以∠B =∠C.
(3)作用:它是证明角相等常用的方法,应用它可省
去三角形全等的证明,因而更简便.
知2-讲
例3 已知:如图,在△ABC中,AB=AC,∠BAC= 120°,点 D,E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
知2-讲
解:∵AB=AC,(已知)
∴∠B=∠C.(等边对等角)
∴∠B=∠C=
又∵ BD=AD,(已知)
∴∠BAD=∠B=30°.(等边对等角)
同理,∠CAE=∠C=30°.
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°.
知2-讲
本例中去掉AB=AC这个条件,能否求得∠DAE的度数?
本题给你怎样的启示?
知2-讲
例4 (1)在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.
导引:给出的条件中,若底角、顶角已确定,可直接运用三角形 的内角和定理与等腰三角形的两底角相等的性质求解;若给出的条件中底角、顶角不确定,则要分两种情况求解.
知2-讲
解:(1)∵AB=AC,∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
(2)当底角为70°时,顶角为180°-70°×2=40°.当顶角为70°时,70°即为所求.因此顶角为40°或70°.
知2-讲
(3)若顶角为90°,则底角为
若底角为90°,则三个内角的和将大于180°,不符合三角形内角和定理.
因此顶角为90°.
知2-讲
在等腰三角形中求角时,要看给出的角是否确
定为顶角或底角.若已确定,则直接利用三角形的
内角和定理求解;若没有指出所给的角是顶角还是
底角,要分两种情况讨论,并看是否符合三角形内
角和定理.若等腰三角形中给出的一内角是直角或
钝角,则此角必为顶角.
知2-讲
例5 (广西贺州)如图,在等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是________.
50°
知2-讲
导引:根据线段垂直平分线上的点到线段两端的距离相等可得AD=BD,根据等边对等角可得∠A=∠ABD,然后表示出∠ABC,再根据等腰三角形两底角相等可得∠C=∠ABC,然后根据三角形的内角和定理列出方程求解即可.
知2-讲
∵MN是AB的垂直平分线,∴AD=BD,
∴∠A=∠ABD,∵∠DBC=15°,
∴∠ABC=∠A+15°,
∵AB=AC,∴∠C=∠ABC=∠A+15°,
∴∠A+∠A+15°+∠A+15°=180°,
解得∠A=50°.
知2-讲
由线段的垂直平分线可以得到相等的线段,运用等腰三角形性质可以将同一个三角形中线段的相等关系转化为所对内角之间的相等关系.
知2-讲
例6 已知:如图,在△ABC中,AB= AC,点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
知2-讲
解:∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,∠A=∠ABD.(等边对等角)
设∠A=x°,则∠BDC=∠A+∠ABD=2x°.
(三角形的一个外角等于与它不相邻的两个内角的和)
∵∠ABC=∠C=∠BDC=2x°,
∴x+ 2x + 2x=180.(三角形内角和等于 180°)
解方程,得x= 36.
∴∠A=36°,∠C=72°.
知2-讲
例7 求证:斜边和一条直角边分别相等的两个直角三角形全等.已知:如图(1),在Rt△ABC和Rt△A'B'C '中,∠C=∠C'=90°,AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
本例是14.2节中已经学过的判定两个直角三角形全等的定理“HL”的证明.
知2-讲
证明:在平面内移动Rt△ABC和Rt△A'B'C',使点A和点A'、点C和点C'重合,点B和点B'在AC的两侧[图(2)].
∵∠BCB'=90°+90°=180°,
(等式性质)
∴B,C,B'三点在一条
直线上.(平角的定义)
知2-讲
证明:在△ABB'中,
∵AB=AB', (已知)
∴∠B=∠B'.(等边对等角)
在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'. (AAS)
知2-练
1
(中考·盐城)若等腰三角形的顶角为40°,则它的底角度数为( )
A.40° B.50° C.60° D.70°
D
知2-练
(中考·湘西州)如图,在等腰三角形ABC中,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
A.36° B.60°
C.72° D.108°
2
C
3
知识点
等边三角形的性质:每个角都等于60°
知3-讲
等边三角形的性质
1.定义:三边都相等的三角形是等边三角形.
要点精析: (1)它是特殊的等腰三角形,具备等腰三角形的所有性质;(2)它是特殊的等腰三角形,任意两边都可以作为腰,任意一个角都可以作为顶角.
知3-讲
2.性质:(1)等边三角形的三边都相等;(2)等边三角形的三个内角相等,每一个内角都等于60°.(3)等边三角形是轴对称图形,它有三条对称轴,分别为三边的垂直平分线;(4)各边上的高、中线、对角的平分线重合,且长度相等.
知3-讲
例8 如图,△ABC是等边三角形,D,E,
F分别是三边AB,AC,BC上的点,
且DE⊥AC,EF⊥BC,DF⊥AB,
计算△DEF各个内角的度数.
知3-讲
导引:
要计算出△DEF各个内角的度数,有两个途径,即证△DEF 为等边三角形或直接求各个内角的度数,由垂直定义及等边三角形的性质,显然直接求各个内角的度数较容易.
知3-讲
解:因为△ABC是等边三角形,
所以∠A=∠B=∠C=60°.
因为DE⊥AC,EF⊥BC,DF⊥AB,
所以∠AED=∠EFC=∠FDB=90°,
所以∠ADE=90°-∠A=90°-60°=30°,
所以∠EDF= 180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
即△DEF各个内角的度数都是60°.
知3-讲
利用等边三角形的性质求角的度数时,通过利用等边三角形三个内角都相等,并且每一个内角都为60°的性质,找出要求角与已知角间的关系来进行计算;有时还要结合全等图形等知识来解决.
知3-讲
例9 如图,已知△ABC,△BDE都是
等边三角形.求证:AE=CD.
导引:要证AE=CD,可通过证分别含
有AE,CD的两个三角形全等
来实现,即证△ABE≌△CBD,所需条件可从等边三角形中去寻找.
知3-讲
证明:∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS).∴AE=CD.
知3-讲
运用等边三角形性质证明线段相等的方法:把要证的两条线段放到一个三角形中证其为等腰或等边三角形或者放到两个三角形中,利用全等三角形的性质证明;注意等边三角形的三个内角相等、三条边相等、三线合一是隐含的已知条件.
知3-讲
例3 如图,△ABC是等边三角形,分别延长AB至点F,BC至点D,CA至点E,使AF=3AB,BD=3BC,CE=3CA,
求证:△DEF是等边三角形.
导引:利用等边三角形定义判定.
知3-讲
证明:∵△ABC是等边三角形,
∴AB=BC=CA,∠BAC=∠ABC
=∠ACB=60°,
∴∠EAF=∠FBD=∠DCE=120°.
又∵AF=3AB,BD=3BC,CE=3CA,
∴AF=BD=CE,AE=BF=CD,
∴△AEF≌△BFD≌△CDE.
∴EF=FD=DE.∴△DEF是等边三角形.
知3-讲
充分挖掘等边三角形中的有关性质是解决问题的前提,然后利用三角形全等得到三边相等,根据定义证得△DEF是等边三角形.
知3-练
如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
1
D
知3-练
如图,一张等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
A.180° B.220°
C.240° D.300°
2
C
1.等腰三角形“三线合一”的性质包含三层含义:
(1)已知等腰三角形底边上的中线,则它平分顶角,垂直于底边;
(2)已知等腰三角形顶角的平分线,则它垂直平分底边;
(3)已知等腰三角形底边上的高,则它平分底边,平分顶角.
2.等腰三角形“三线合一”的性质常常可以用来证明角相等、线段相等和线段垂直.在遇到等腰三角形的问题时,尝试作这条辅助线,常常会有意想不到的效果.
请完成对应习题。
第15章 轴对称图形与等腰三角形
第3节 等腰三角形
等腰三角形的性质
课堂讲解
课时流程
1
2
等腰三角形的轴对称性、三线合一
等腰三角形的边角性质:等边对等角
等边三角形的性质:每个角都等于60°
逐点
导讲练
课堂小结
课后
作业
等腰三角形是一类特殊的三角形.等腰三角形除具有一般三角形的性质外,还具有什么样的特殊性质呢?
1
知识点
等腰三角形的轴对称性、三线合一
知1-讲
等腰三角形的轴对称性:“三线合一”
定理1:等腰三角形顶角的平分线垂直平分底边.
结论:等腰三角形顶角的平分线、底边上的中线、底边上的高相 互重合(简称“三线合一”).
知1-讲
要点精析:
(1)含义:这是等腰三角形所特有的性质,它实际是一组定理,应用过程中,在三角形是等腰三角形前提下,“顶角的平分线、底边上的中线、底边上的高”只要知道其中“一线”,就可以说明是其他“两线”.
知1-讲
(3)对称性:等腰三角形是轴对称图形,顶角平分线(或底边上的高、底边上的中线)所在的直线是它的对称轴.
(2)作用:是证明线段相等、角相等、垂直等关系的重要方法,应用广泛.
知1-讲
(4)应用格式:如图,在△ABC中,
①∵AB=AC,AD⊥BC,∴AD平分
∠BAC(或BD=CD);
②∵AB=AC,BD=DC,∴AD⊥BC(或AD平分∠BAC);
③∵AB=AC,AD平分∠BAC,∴BD=DC(或AD⊥BC).
知1-讲
例1 如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
知1-讲
解: (1) ∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,
∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴ ∠C=∠ABC=
知1-讲
证明: (2) ∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∴∠BDE=90°.
∵EF⊥AB,
∴∠BFE=90°,∴∠BFE=∠BDE.
又∵BG平分∠ABC,∴∠FBE=∠DBE.
∵BE为公共边,
∴△BDE≌△BFE,∴EF=ED.
知1-讲
等腰三角形“三线合一”的性质是证明角相等、线段相等和垂直关系的既重要又简便的方法;因为题目的证明或计算所求结果大多都是单一的,所以“三线合一”的性质的应用也是单一的,一般得出一个结论,因此应用要灵活.在等腰三角形中,作“三线”中“一线”,利用“三线合一”是等腰三角形中常用的方法.
知1-讲
例2 如图所示,AB=AE,BC=DE,∠B=∠E, AM⊥CD,垂足为M.求证:CM=MD.
导引:由已知AM⊥CD和结论CM=MD,
联想到等腰三角形“三线合一”
的性质,由此连接AC,AD构造
等腰三角形.
知1-讲
证明:如图,连接AC,AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).∴AC=AD.
又∵AM⊥CD,∴CM=MD.
知1-讲
对于单一等腰三角形构造“三线合一”的基本图形,作底边上的高、中线还是顶角平分线,可根据解题需要作辅助线;对于叠合等腰三角形构造“三线合一”的基本图形,则需巧作辅助线,下面就如下几种图形说明巧作辅助线的方法:
知1-讲
知1-讲
1.如图甲的情形,需作底边上的高;
2.如图乙的情形,需作顶角平分线;
3.如图丙的情形,需作中线;
4.如图丁的情形,需连接AD并延长再证其是“三线”即可.
知1-练
1
如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;②DE=DF;③BD=CD;④若点P在直线AD上,则PB=PC.
其中正确的是( )
A.① B.①②
C.①②③ D.①②③④
D
2
知识点
等腰三角形的边角性质:等边对等角
知2-讲
操作
画一个等腰三角形ABC,如图(1).把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.
知2-讲
操作
如图(2).观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?
AD与BC垂直吗?为什么?
等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴.
知2-讲
等腰三角形的边角性质:等边对等角
定理1:等腰三角形的两底角相等(简称“等边对等角”).
要点精析:
(1)适用条件:必须在同一个三角形中.
(2)应用格式:在△ABC中,因为AB=AC,所以∠B =∠C.
(3)作用:它是证明角相等常用的方法,应用它可省
去三角形全等的证明,因而更简便.
知2-讲
例3 已知:如图,在△ABC中,AB=AC,∠BAC= 120°,点 D,E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
知2-讲
解:∵AB=AC,(已知)
∴∠B=∠C.(等边对等角)
∴∠B=∠C=
又∵ BD=AD,(已知)
∴∠BAD=∠B=30°.(等边对等角)
同理,∠CAE=∠C=30°.
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°.
知2-讲
本例中去掉AB=AC这个条件,能否求得∠DAE的度数?
本题给你怎样的启示?
知2-讲
例4 (1)在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.
导引:给出的条件中,若底角、顶角已确定,可直接运用三角形 的内角和定理与等腰三角形的两底角相等的性质求解;若给出的条件中底角、顶角不确定,则要分两种情况求解.
知2-讲
解:(1)∵AB=AC,∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
(2)当底角为70°时,顶角为180°-70°×2=40°.当顶角为70°时,70°即为所求.因此顶角为40°或70°.
知2-讲
(3)若顶角为90°,则底角为
若底角为90°,则三个内角的和将大于180°,不符合三角形内角和定理.
因此顶角为90°.
知2-讲
在等腰三角形中求角时,要看给出的角是否确
定为顶角或底角.若已确定,则直接利用三角形的
内角和定理求解;若没有指出所给的角是顶角还是
底角,要分两种情况讨论,并看是否符合三角形内
角和定理.若等腰三角形中给出的一内角是直角或
钝角,则此角必为顶角.
知2-讲
例5 (广西贺州)如图,在等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是________.
50°
知2-讲
导引:根据线段垂直平分线上的点到线段两端的距离相等可得AD=BD,根据等边对等角可得∠A=∠ABD,然后表示出∠ABC,再根据等腰三角形两底角相等可得∠C=∠ABC,然后根据三角形的内角和定理列出方程求解即可.
知2-讲
∵MN是AB的垂直平分线,∴AD=BD,
∴∠A=∠ABD,∵∠DBC=15°,
∴∠ABC=∠A+15°,
∵AB=AC,∴∠C=∠ABC=∠A+15°,
∴∠A+∠A+15°+∠A+15°=180°,
解得∠A=50°.
知2-讲
由线段的垂直平分线可以得到相等的线段,运用等腰三角形性质可以将同一个三角形中线段的相等关系转化为所对内角之间的相等关系.
知2-讲
例6 已知:如图,在△ABC中,AB= AC,点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
知2-讲
解:∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,∠A=∠ABD.(等边对等角)
设∠A=x°,则∠BDC=∠A+∠ABD=2x°.
(三角形的一个外角等于与它不相邻的两个内角的和)
∵∠ABC=∠C=∠BDC=2x°,
∴x+ 2x + 2x=180.(三角形内角和等于 180°)
解方程,得x= 36.
∴∠A=36°,∠C=72°.
知2-讲
例7 求证:斜边和一条直角边分别相等的两个直角三角形全等.已知:如图(1),在Rt△ABC和Rt△A'B'C '中,∠C=∠C'=90°,AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
本例是14.2节中已经学过的判定两个直角三角形全等的定理“HL”的证明.
知2-讲
证明:在平面内移动Rt△ABC和Rt△A'B'C',使点A和点A'、点C和点C'重合,点B和点B'在AC的两侧[图(2)].
∵∠BCB'=90°+90°=180°,
(等式性质)
∴B,C,B'三点在一条
直线上.(平角的定义)
知2-讲
证明:在△ABB'中,
∵AB=AB', (已知)
∴∠B=∠B'.(等边对等角)
在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'. (AAS)
知2-练
1
(中考·盐城)若等腰三角形的顶角为40°,则它的底角度数为( )
A.40° B.50° C.60° D.70°
D
知2-练
(中考·湘西州)如图,在等腰三角形ABC中,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
A.36° B.60°
C.72° D.108°
2
C
3
知识点
等边三角形的性质:每个角都等于60°
知3-讲
等边三角形的性质
1.定义:三边都相等的三角形是等边三角形.
要点精析: (1)它是特殊的等腰三角形,具备等腰三角形的所有性质;(2)它是特殊的等腰三角形,任意两边都可以作为腰,任意一个角都可以作为顶角.
知3-讲
2.性质:(1)等边三角形的三边都相等;(2)等边三角形的三个内角相等,每一个内角都等于60°.(3)等边三角形是轴对称图形,它有三条对称轴,分别为三边的垂直平分线;(4)各边上的高、中线、对角的平分线重合,且长度相等.
知3-讲
例8 如图,△ABC是等边三角形,D,E,
F分别是三边AB,AC,BC上的点,
且DE⊥AC,EF⊥BC,DF⊥AB,
计算△DEF各个内角的度数.
知3-讲
导引:
要计算出△DEF各个内角的度数,有两个途径,即证△DEF 为等边三角形或直接求各个内角的度数,由垂直定义及等边三角形的性质,显然直接求各个内角的度数较容易.
知3-讲
解:因为△ABC是等边三角形,
所以∠A=∠B=∠C=60°.
因为DE⊥AC,EF⊥BC,DF⊥AB,
所以∠AED=∠EFC=∠FDB=90°,
所以∠ADE=90°-∠A=90°-60°=30°,
所以∠EDF= 180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
即△DEF各个内角的度数都是60°.
知3-讲
利用等边三角形的性质求角的度数时,通过利用等边三角形三个内角都相等,并且每一个内角都为60°的性质,找出要求角与已知角间的关系来进行计算;有时还要结合全等图形等知识来解决.
知3-讲
例9 如图,已知△ABC,△BDE都是
等边三角形.求证:AE=CD.
导引:要证AE=CD,可通过证分别含
有AE,CD的两个三角形全等
来实现,即证△ABE≌△CBD,所需条件可从等边三角形中去寻找.
知3-讲
证明:∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS).∴AE=CD.
知3-讲
运用等边三角形性质证明线段相等的方法:把要证的两条线段放到一个三角形中证其为等腰或等边三角形或者放到两个三角形中,利用全等三角形的性质证明;注意等边三角形的三个内角相等、三条边相等、三线合一是隐含的已知条件.
知3-讲
例3 如图,△ABC是等边三角形,分别延长AB至点F,BC至点D,CA至点E,使AF=3AB,BD=3BC,CE=3CA,
求证:△DEF是等边三角形.
导引:利用等边三角形定义判定.
知3-讲
证明:∵△ABC是等边三角形,
∴AB=BC=CA,∠BAC=∠ABC
=∠ACB=60°,
∴∠EAF=∠FBD=∠DCE=120°.
又∵AF=3AB,BD=3BC,CE=3CA,
∴AF=BD=CE,AE=BF=CD,
∴△AEF≌△BFD≌△CDE.
∴EF=FD=DE.∴△DEF是等边三角形.
知3-讲
充分挖掘等边三角形中的有关性质是解决问题的前提,然后利用三角形全等得到三边相等,根据定义证得△DEF是等边三角形.
知3-练
如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
1
D
知3-练
如图,一张等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
A.180° B.220°
C.240° D.300°
2
C
1.等腰三角形“三线合一”的性质包含三层含义:
(1)已知等腰三角形底边上的中线,则它平分顶角,垂直于底边;
(2)已知等腰三角形顶角的平分线,则它垂直平分底边;
(3)已知等腰三角形底边上的高,则它平分底边,平分顶角.
2.等腰三角形“三线合一”的性质常常可以用来证明角相等、线段相等和线段垂直.在遇到等腰三角形的问题时,尝试作这条辅助线,常常会有意想不到的效果.
请完成对应习题。
