沪科版八上数学15.3 等腰三角形-- 含30°角的直角三角形的性质教学课件(23张)
文档属性
| 名称 | 沪科版八上数学15.3 等腰三角形-- 含30°角的直角三角形的性质教学课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 917.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第15章 轴对称图形与等腰三角形
第3节 等腰三角形
含30°角的直角三角形的性质
课堂讲解
课时流程
1
2
含30°角的直角三角形的性质
含30°角的直角三角形的性质的应用
逐点
导讲练
课堂小结
课后
作业
1
知识点
含30°角的直角三角形的性质
知1-讲
1.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
要点精析: (1)适用条件——含30°角的直角三角形,
(2)揭示的关系——30°角所对的直角边与斜边的关系.
知1-讲
2.拓展:在直角三角形中,若一直角边等于斜边的一半,则该直角边所对的角为30°.
3.作用:应用于证线段的倍分关系和计算角度.
知1-讲
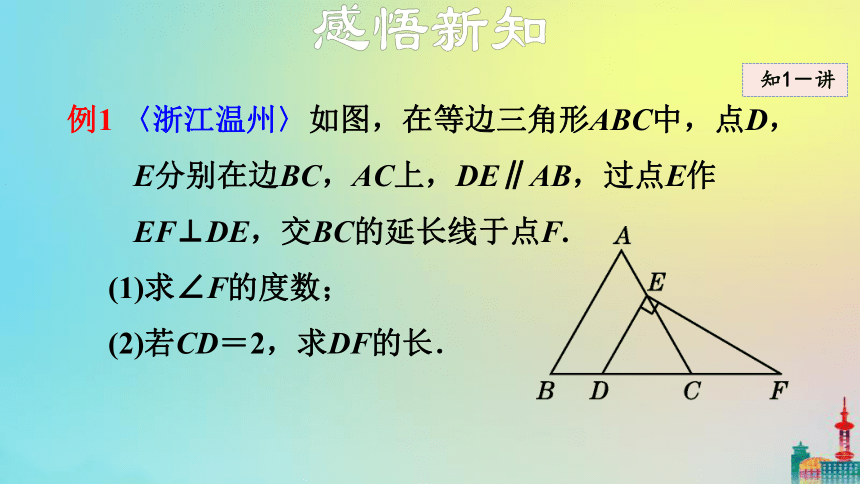
例1 〈浙江温州〉如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
知1-讲
导引:(1)根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求解;(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
知1-讲
解:(1)∵△ABC是等边三角形,∴∠B=60°,
∵DE∥AB,∴∠EDC=∠B=60°,
∵EF⊥DE,∴∠DEF=90°,
∴∠F=90°-∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴∠DEC=60°, ∴△EDC是等边三角形.
∴ED=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.
知1-讲
利用含30°角的直角三角形的性质,关键有两个要素:一是30°的角;二是直角三角形.根据这两个要素可建立直角三角形中斜边与直角边之间的关系.
知1-讲
例2 如图,在等边三角形ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,求证:BP=2PQ.
导引:由于BQ⊥AD,要证BP=2PQ,
只需证∠PBQ=30°,根据已知可 证△ABE≌△CAD,故∠CAD=∠ABE,结合等边三角形的内角可证∠BPQ=60°.
知1-讲
证明:在等边三角形ABC中,AB=AC,
∠BAE=∠C=60°.
∵AE=CD,∴△ABE≌△CAD,
∴∠CAD=∠ABE, ∴∠BPQ=
∠ABE+∠BAP=∠CAD+∠BAP
=∠BAE=60°.
∵BQ⊥AD,∴∠PBQ=30°,∴BP=2PQ.
知1-讲
60°角的余角是30°,当问题中出现直角及30°角时,经常利用“在直角三角形中,30°角所对的直角边等于斜边的一半”的性质来解决线段的倍分问题.
知1-练
1
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,则AB等于( )
A.6 cm B.7 cm C.8 cm D.9 cm
C
知1-练
2
如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,垂足为D,BE=6 cm,则AC等于( )
A.6 cm B.5 cm
C.4 cm D.3 cm
D
2
知识点
含30°角的直角三角形的性质的应用
知2-讲
例3 如图,一艘船从A处出发,以每时10n mile(海里)的速度向正北航行,从A处测得一礁石
C在北偏西30°的方向上.如果这艘船
上午8:00从A处出发,10:00到达B处,
从B处测得礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;(2)求从B处到礁石C的距离.
知2-讲
解:(1)以B为顶点,向北偏西60°作角,这角一边与AC交于点C, 则点C为礁石所在地.
知2-讲
解: (2)∵∠ACB= 60°-30°=30°,(三角形的外角性质)
又∵∠BAC= 30°,∴∠BCA=∠BAC. ∴BC=BA.
∵BA=10×(10-8)=20(n mile),
∴BC=20(n mile).
即从 B处到礁石C的距离是20n mile.
知2-练
1
如图是屋架设计图的一部分,立柱BC垂直于横梁AD,AB=8 m,∠A=30°,则立柱BC的长度为( )
A.4 m B.8 m
C.10 m D.16 m
A
知2-练
2
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( )
A.3 m B.4 m
C.5 m D.6 m
B
知2-练
3
如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为________米.
12
知2-练
4
将一副三角尺如图叠放在一起,若AB=10 cm,则阴影部分的面积是________cm2.
1.在直角三角形中,30°角所对的直角边等于斜边的一半.这个定理将特殊的直角三角形中的角度关系转化为直角三角形中边的等量关系.在一般情况下,遇到30°角常用的添加辅助线的方法就是作垂线,构造含30°角的直角三角形,解决相关的线段问题.
2.利用含30°角的直角三角形的性质求有关线段的长:
依据:直角三角形中30°角所对的直角边等于斜边的一半.
用途:求线段长度和证明线段倍分关系.
作法:当图形中含有30°角时,通过作垂线构造含有30°角的直角三角形.
请完成对应习题。
第15章 轴对称图形与等腰三角形
第3节 等腰三角形
含30°角的直角三角形的性质
课堂讲解
课时流程
1
2
含30°角的直角三角形的性质
含30°角的直角三角形的性质的应用
逐点
导讲练
课堂小结
课后
作业
1
知识点
含30°角的直角三角形的性质
知1-讲
1.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
要点精析: (1)适用条件——含30°角的直角三角形,
(2)揭示的关系——30°角所对的直角边与斜边的关系.
知1-讲
2.拓展:在直角三角形中,若一直角边等于斜边的一半,则该直角边所对的角为30°.
3.作用:应用于证线段的倍分关系和计算角度.
知1-讲
例1 〈浙江温州〉如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
知1-讲
导引:(1)根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求解;(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
知1-讲
解:(1)∵△ABC是等边三角形,∴∠B=60°,
∵DE∥AB,∴∠EDC=∠B=60°,
∵EF⊥DE,∴∠DEF=90°,
∴∠F=90°-∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴∠DEC=60°, ∴△EDC是等边三角形.
∴ED=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.
知1-讲
利用含30°角的直角三角形的性质,关键有两个要素:一是30°的角;二是直角三角形.根据这两个要素可建立直角三角形中斜边与直角边之间的关系.
知1-讲
例2 如图,在等边三角形ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,求证:BP=2PQ.
导引:由于BQ⊥AD,要证BP=2PQ,
只需证∠PBQ=30°,根据已知可 证△ABE≌△CAD,故∠CAD=∠ABE,结合等边三角形的内角可证∠BPQ=60°.
知1-讲
证明:在等边三角形ABC中,AB=AC,
∠BAE=∠C=60°.
∵AE=CD,∴△ABE≌△CAD,
∴∠CAD=∠ABE, ∴∠BPQ=
∠ABE+∠BAP=∠CAD+∠BAP
=∠BAE=60°.
∵BQ⊥AD,∴∠PBQ=30°,∴BP=2PQ.
知1-讲
60°角的余角是30°,当问题中出现直角及30°角时,经常利用“在直角三角形中,30°角所对的直角边等于斜边的一半”的性质来解决线段的倍分问题.
知1-练
1
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,则AB等于( )
A.6 cm B.7 cm C.8 cm D.9 cm
C
知1-练
2
如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,垂足为D,BE=6 cm,则AC等于( )
A.6 cm B.5 cm
C.4 cm D.3 cm
D
2
知识点
含30°角的直角三角形的性质的应用
知2-讲
例3 如图,一艘船从A处出发,以每时10n mile(海里)的速度向正北航行,从A处测得一礁石
C在北偏西30°的方向上.如果这艘船
上午8:00从A处出发,10:00到达B处,
从B处测得礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;(2)求从B处到礁石C的距离.
知2-讲
解:(1)以B为顶点,向北偏西60°作角,这角一边与AC交于点C, 则点C为礁石所在地.
知2-讲
解: (2)∵∠ACB= 60°-30°=30°,(三角形的外角性质)
又∵∠BAC= 30°,∴∠BCA=∠BAC. ∴BC=BA.
∵BA=10×(10-8)=20(n mile),
∴BC=20(n mile).
即从 B处到礁石C的距离是20n mile.
知2-练
1
如图是屋架设计图的一部分,立柱BC垂直于横梁AD,AB=8 m,∠A=30°,则立柱BC的长度为( )
A.4 m B.8 m
C.10 m D.16 m
A
知2-练
2
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( )
A.3 m B.4 m
C.5 m D.6 m
B
知2-练
3
如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为________米.
12
知2-练
4
将一副三角尺如图叠放在一起,若AB=10 cm,则阴影部分的面积是________cm2.
1.在直角三角形中,30°角所对的直角边等于斜边的一半.这个定理将特殊的直角三角形中的角度关系转化为直角三角形中边的等量关系.在一般情况下,遇到30°角常用的添加辅助线的方法就是作垂线,构造含30°角的直角三角形,解决相关的线段问题.
2.利用含30°角的直角三角形的性质求有关线段的长:
依据:直角三角形中30°角所对的直角边等于斜边的一半.
用途:求线段长度和证明线段倍分关系.
作法:当图形中含有30°角时,通过作垂线构造含有30°角的直角三角形.
请完成对应习题。
