人教版高中数学必修1第三章第一节方程的根与函数的零点(共18张PPT)
文档属性
| 名称 | 人教版高中数学必修1第三章第一节方程的根与函数的零点(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 584.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
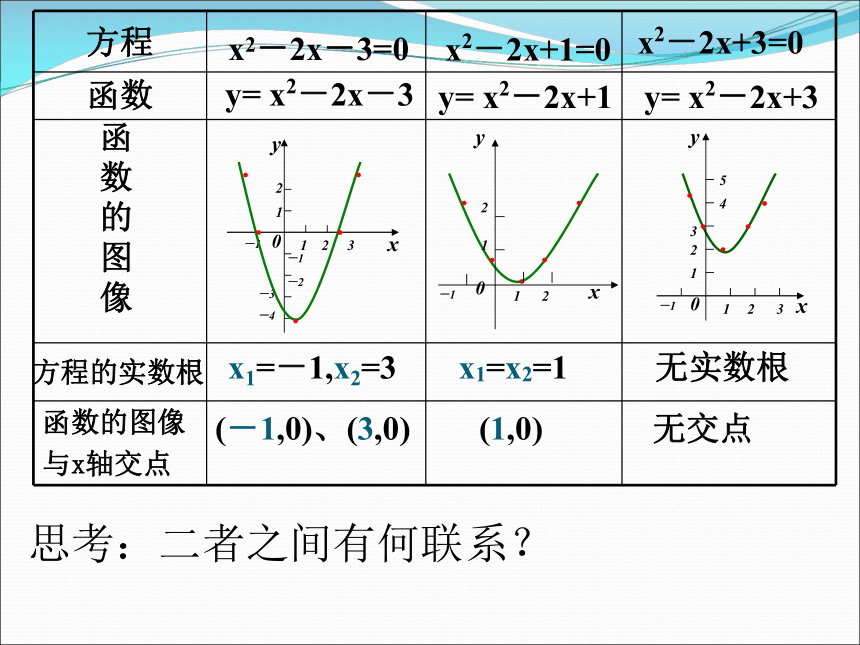
方程
函数
函
数
的
图像
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
函数的图像
与x轴交点
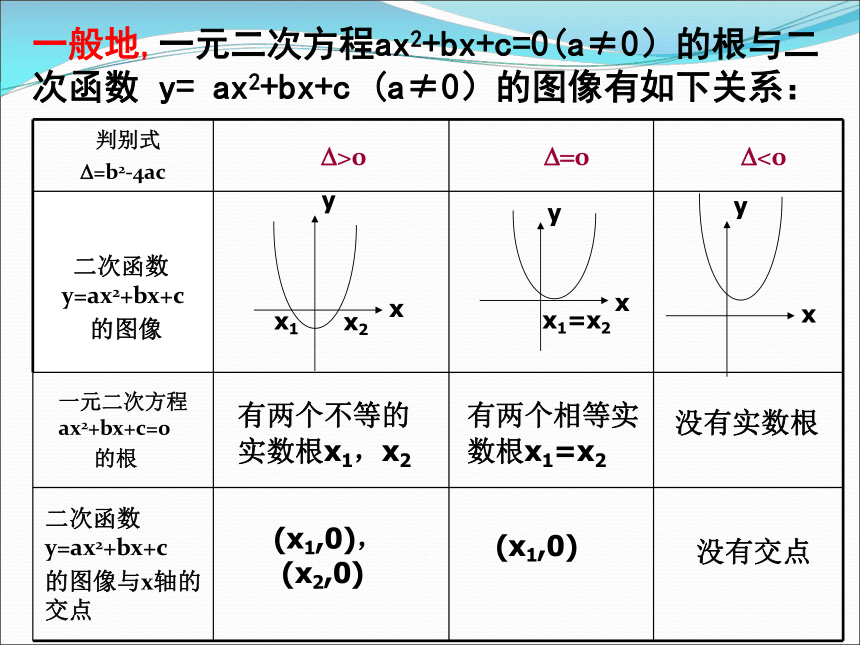
有两个不等的
实数根x1,x2
有两个相等实数根x1=x2
没有实数根
一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图像有如下关系:
(x1,0),
(x2,0)
(x1,0)
没有交点
判别式
?=b2-4ac ?>0 ??0 ?<0
二次函数y=ax2+bx+c
的图像
一元二次方程ax2+bx+c=0
的根
二次函数y=ax2+bx+c
的图像与x轴的交点
1、函数零点的定义
方程f(x)=0有实数根
2、结论
问题6:如果将定义域改为区间[a,b]观察图像
说一说零点个数的情况,有什么发现?
问题8:满足上述两个条件,能否确定零点
个数呢?
结论
表3--1
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972
问题10:为什么上个问题中只有一个零点呢?
说一说理由?
练习:88页第一题
问题11:请同学们思考、交流一下,这节课
学习到了什么?
1、知识小结:一个定义,四个结论。
2、思想方法:数形结合、转化思想。
作业:
1、必做题:P88 练习第二题
方程
函数
函
数
的
图像
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
函数的图像
与x轴交点
有两个不等的
实数根x1,x2
有两个相等实数根x1=x2
没有实数根
一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图像有如下关系:
(x1,0),
(x2,0)
(x1,0)
没有交点
判别式
?=b2-4ac ?>0 ??0 ?<0
二次函数y=ax2+bx+c
的图像
一元二次方程ax2+bx+c=0
的根
二次函数y=ax2+bx+c
的图像与x轴的交点
1、函数零点的定义
方程f(x)=0有实数根
2、结论
问题6:如果将定义域改为区间[a,b]观察图像
说一说零点个数的情况,有什么发现?
问题8:满足上述两个条件,能否确定零点
个数呢?
结论
表3--1
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972
问题10:为什么上个问题中只有一个零点呢?
说一说理由?
练习:88页第一题
问题11:请同学们思考、交流一下,这节课
学习到了什么?
1、知识小结:一个定义,四个结论。
2、思想方法:数形结合、转化思想。
作业:
1、必做题:P88 练习第二题
