高中数学人教A版必修3第二章2.2.1用样本的频率分布估计总体分布(2)课件(共17张PPT)
文档属性
| 名称 | 高中数学人教A版必修3第二章2.2.1用样本的频率分布估计总体分布(2)课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 676.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
2.2.1用样本的频率分布估计总体分布(二)
(频率分布折线图、总体密度曲线、茎叶图)
复习:画频率分布直方图的步骤
①找最大值与最小值。
②决定组距与组数
③决定分点
④登记频数,计算频率,列表,画直方图
本课中的基本概念
一、 众数、中位数、平均数的概念:
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.众数是零个或多个.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
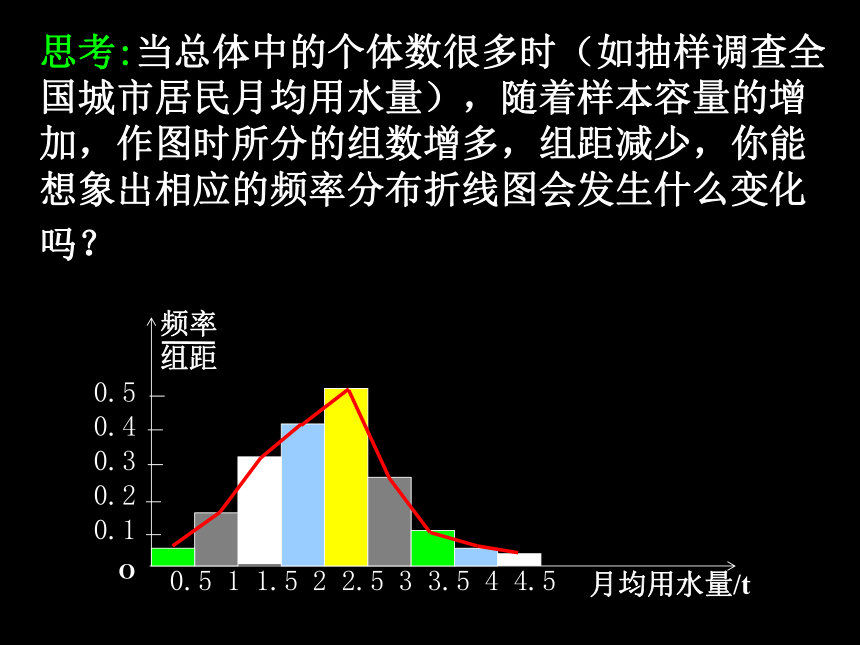
在频率分布直方图中,依次连接各小长方形上端的中点,就得到一条折线,这条折线称为频率分布折线图. 你认为频率分布折线图能大致反映样本数据的频率分布吗?
二、频率分布折线图
思考:当总体中的个体数很多时(如抽样调查全国城市居民月均用水量),随着样本容量的增加,作图时所分的组数增多,组距减少,你能想象出相应的频率分布折线图会发生什么变化吗?
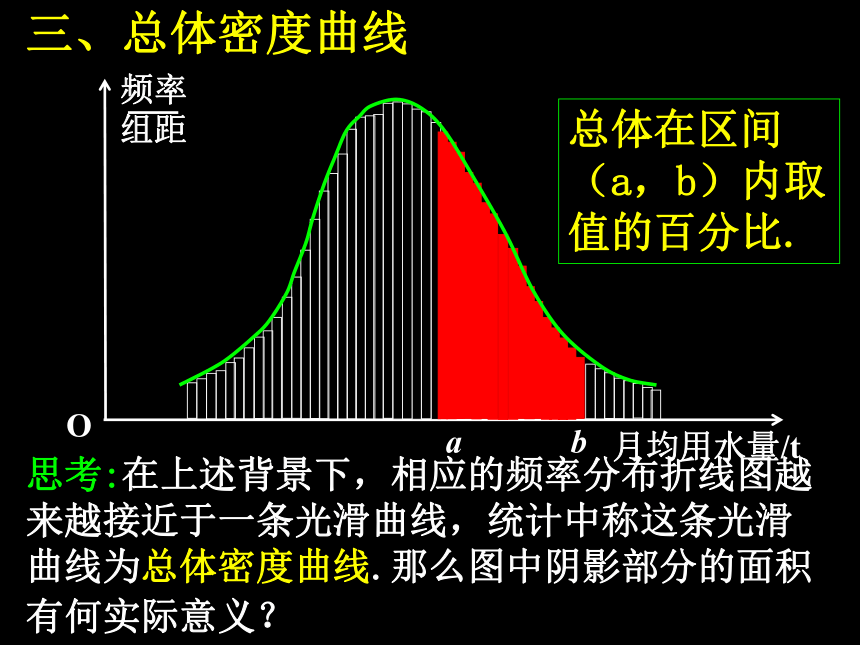
思考:在上述背景下,相应的频率分布折线图越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.那么图中阴影部分的面积有何实际意义?
总体在区间(a,b)内取值的百分比.
三、总体密度曲线
思考1:当总体中的个体数比较少或样
本数据不密集时,是否存在总体密度曲线?为什么?
不存在,因为组距不能任意缩小.
思考2:对于一个总体,如果存在总体密度曲线,这条曲线是否惟一?能否通过样本数据准确地画出总体密度曲线?
四、茎叶图
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39
乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39
(1)画出茎叶图;(2)根据茎叶图分析这两名运动员的水平。
茎叶图
甲
乙
0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
0
8
4 6 3
6 8
3 8 9
1
叶就是从茎的旁边生长出来的数,表示得分的个位数。
茎是指中间的一列数,表示得分的十位数
画茎叶图的步骤:
1、将每个数据分为茎(高位)和叶(低位)两部分,再此例中,茎为十位上的数字,叶为个位上的数字。
2、将最小茎和最大茎之间的数按大小次序排成一行,写在左(右)侧。
3、将各个数据的叶按大小次序写在其茎的右(左)侧。
几种表示频率分布的方法的优点和不足
(1)频率分布表在数量表示上比较确切,但不够直观、形象,分析数据分布的总体态势不太方便。
(2)频率分布直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到在分布表中看不清楚的数据模式。缺点是原始数据不能在图中表示。
(3)频率分布折线图的优点是它反映了数据的变化趋势。如果样本容量不断增大,分组的组距不断缩小,那么折线图就趋近于总体分布的密度曲线。
(4)用茎叶图刻画有两个优点:一是所有的信息都可以从这个茎叶图中得到;二是便于记录和表示,能够展示数据的分布情况。但样本数据教多或数据位数较多时,茎叶图就显得不太方便。
(1) 右面是甲、乙两名运动员某赛季一些场次得分的茎叶图,据图可知 ( )
B.乙运动员的成绩好于甲运动员
C.甲、乙两名运动员的成绩没有明显的差异
D.甲运动员的最低得分为0分
A.甲运动员的成绩好于乙运动员
A
知识迁移
(1)频率分布表:
1.00
0.02
0.08
0.09
0.18
0.28
0.15
0.10
0.06
0.04
(2)频率分布直方图:
(3)(0.02+0.08+0.09)×500=95(人)
(3)估计该校学生身高小于134cm的人数约为多少?
例2 为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率分布直方图.图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.
(1)第二小组的频
率是多少?
(2)样本容量是多
少?
(3)若次数在110以
上(含110次)为达
标,试估计该校全体
高一学生的达标率约
是多少?
小结
1.用样本的频率分布估计总体分布,当总体中的个体数取值很少时,可用茎叶图估计总体分布;当总体中的个体数取值较多时,可将样本数据适当分组,用频率分布表或频率分布直方图估计总体分布.
2.总体密度曲线可看成是函数的图象,对一
些特殊的密度曲线,其函数解析式是可求的.
3.茎叶图中数据的茎和叶的划分,可根据样本数据的特点灵活决定.
2.2.1用样本的频率分布估计总体分布(二)
(频率分布折线图、总体密度曲线、茎叶图)
复习:画频率分布直方图的步骤
①找最大值与最小值。
②决定组距与组数
③决定分点
④登记频数,计算频率,列表,画直方图
本课中的基本概念
一、 众数、中位数、平均数的概念:
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.众数是零个或多个.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
在频率分布直方图中,依次连接各小长方形上端的中点,就得到一条折线,这条折线称为频率分布折线图. 你认为频率分布折线图能大致反映样本数据的频率分布吗?
二、频率分布折线图
思考:当总体中的个体数很多时(如抽样调查全国城市居民月均用水量),随着样本容量的增加,作图时所分的组数增多,组距减少,你能想象出相应的频率分布折线图会发生什么变化吗?
思考:在上述背景下,相应的频率分布折线图越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.那么图中阴影部分的面积有何实际意义?
总体在区间(a,b)内取值的百分比.
三、总体密度曲线
思考1:当总体中的个体数比较少或样
本数据不密集时,是否存在总体密度曲线?为什么?
不存在,因为组距不能任意缩小.
思考2:对于一个总体,如果存在总体密度曲线,这条曲线是否惟一?能否通过样本数据准确地画出总体密度曲线?
四、茎叶图
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39
乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39
(1)画出茎叶图;(2)根据茎叶图分析这两名运动员的水平。
茎叶图
甲
乙
0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
0
8
4 6 3
6 8
3 8 9
1
叶就是从茎的旁边生长出来的数,表示得分的个位数。
茎是指中间的一列数,表示得分的十位数
画茎叶图的步骤:
1、将每个数据分为茎(高位)和叶(低位)两部分,再此例中,茎为十位上的数字,叶为个位上的数字。
2、将最小茎和最大茎之间的数按大小次序排成一行,写在左(右)侧。
3、将各个数据的叶按大小次序写在其茎的右(左)侧。
几种表示频率分布的方法的优点和不足
(1)频率分布表在数量表示上比较确切,但不够直观、形象,分析数据分布的总体态势不太方便。
(2)频率分布直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到在分布表中看不清楚的数据模式。缺点是原始数据不能在图中表示。
(3)频率分布折线图的优点是它反映了数据的变化趋势。如果样本容量不断增大,分组的组距不断缩小,那么折线图就趋近于总体分布的密度曲线。
(4)用茎叶图刻画有两个优点:一是所有的信息都可以从这个茎叶图中得到;二是便于记录和表示,能够展示数据的分布情况。但样本数据教多或数据位数较多时,茎叶图就显得不太方便。
(1) 右面是甲、乙两名运动员某赛季一些场次得分的茎叶图,据图可知 ( )
B.乙运动员的成绩好于甲运动员
C.甲、乙两名运动员的成绩没有明显的差异
D.甲运动员的最低得分为0分
A.甲运动员的成绩好于乙运动员
A
知识迁移
(1)频率分布表:
1.00
0.02
0.08
0.09
0.18
0.28
0.15
0.10
0.06
0.04
(2)频率分布直方图:
(3)(0.02+0.08+0.09)×500=95(人)
(3)估计该校学生身高小于134cm的人数约为多少?
例2 为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率分布直方图.图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.
(1)第二小组的频
率是多少?
(2)样本容量是多
少?
(3)若次数在110以
上(含110次)为达
标,试估计该校全体
高一学生的达标率约
是多少?
小结
1.用样本的频率分布估计总体分布,当总体中的个体数取值很少时,可用茎叶图估计总体分布;当总体中的个体数取值较多时,可将样本数据适当分组,用频率分布表或频率分布直方图估计总体分布.
2.总体密度曲线可看成是函数的图象,对一
些特殊的密度曲线,其函数解析式是可求的.
3.茎叶图中数据的茎和叶的划分,可根据样本数据的特点灵活决定.
