青岛版数学七年级下册:13.1 三角形有关概念课件(共24张PPT)
文档属性
| 名称 | 青岛版数学七年级下册:13.1 三角形有关概念课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
图片中有一种共同的平面图形,你发现了吗?
学习目标:
1、经历从具体情境中抽象出三角形建立几何模型的过程,能规范说出三角形的定义和构成。
2、能把三角形按一定的标准进行分类,培养不重不漏的分类思想。
活动二:归纳定义 规范表示
背景
定义、表示
划分(以角、边为标准)
性质(从角、边的角度研究)
特殊三角形(性质和判定)
应用
中学三角形的学习将从以下几个方面展开
本节目标
1、什么叫三角形?
怎么表示一个三角形?
2、什么叫三角形的边?
3、什么叫三角形的顶点?
4、什么叫三角形的角?
课本130页
三角形的构成
三角形
由不在同一条直线上的三条线段
首尾顺次相接所组成的图形。
三角形的边
组成三角形的线段
三角形的顶点
相邻两边的公共端点
A
B
C
三角形的内角
相邻两边所组成的角
学
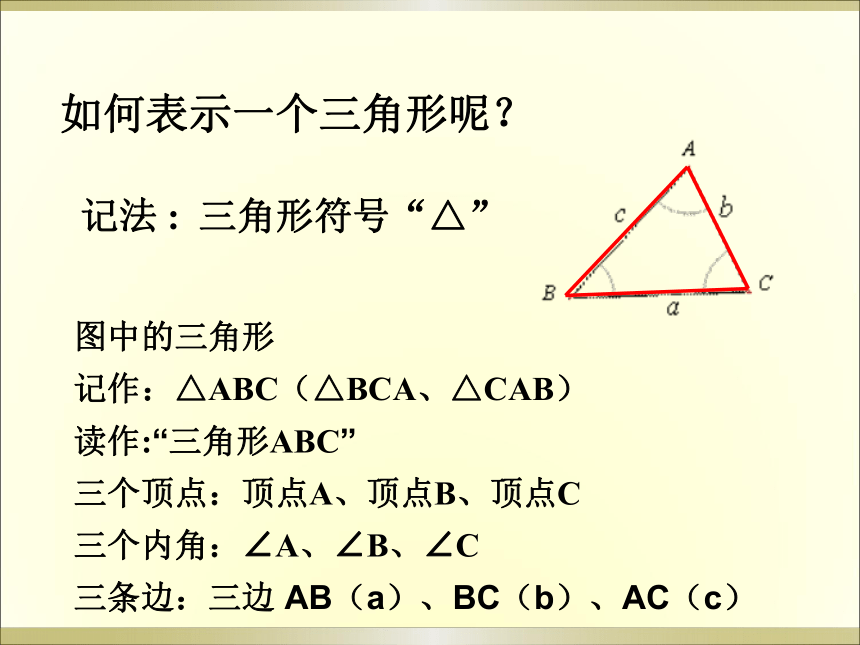
如何表示一个三角形呢?
记法 : 三角形符号“△”
图中的三角形
记作:△ABC(△BCA、△CAB)
读作:“三角形ABC”
三个顶点:顶点A、顶点B、顶点C
三个内角:∠A、∠B、∠C
三条边:三边 AB(a)、BC(b)、AC(c)
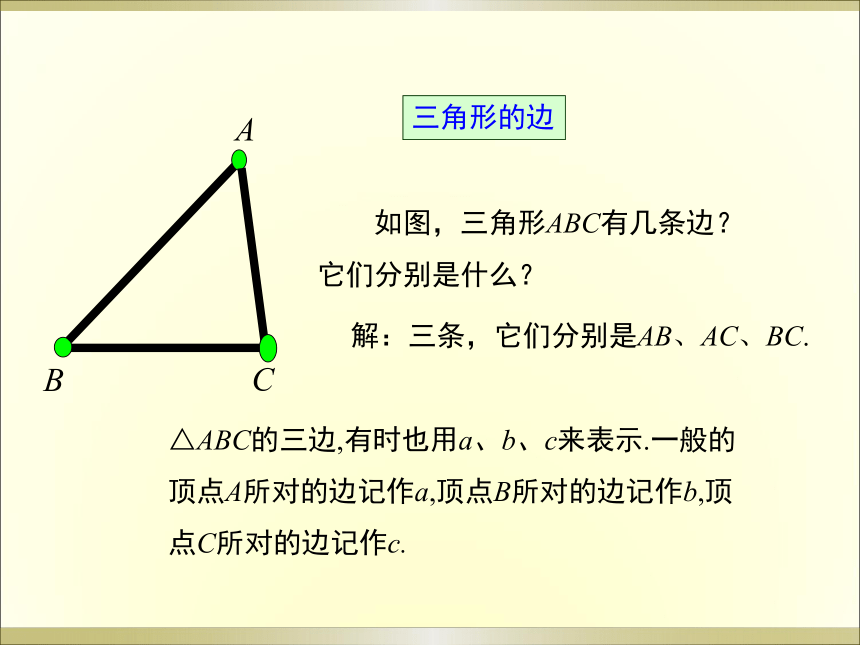
如图,三角形ABC有几条边?它们分别是什么?
△ABC的三边,有时也用a、b、c来表示.一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
解:三条,它们分别是AB、AC、BC.
三角形的边
A
1、图中有 个三角形,并分别用字母表示出来 。
2、 ∠AED是 的角?
3、AE 和 的公共边?
4、 ∠D是 和 的公共角?
D
C
B
E
A
锐角三角形
直角三角形
钝角三角形
三角形
锐角三角形
直角三角形
钝角三角形
把所有的三角形看作一个整体,锐角三角形、直角三角形和钝角三角形都是这个整体的一部分。它们之间的关系,可以用下图表示。
直角三角形各边名称
如图所示:
直角三角形通常用符号
“Rt△”表示.如图所示
直角三角形记Rt△ABC.
在直角三角形中三边中,哪条边最长?为什么?
直角三角形的两个锐角互余。
符号语言:在Rt△ABC中, ∠ C= 90° ∠ A+ ∠ B= 90°
1、锐角三角形的三个内角都是锐角;( )
2、钝角三角形的三个内角都是钝角;( )
3、直角三角形的斜边大于任何一条直角边;( )
4、三角形中至少有两个锐角;( )
5、三角形的三个内角中,最多有一个是钝角。
( )
判断题(对的填“√”,错的填“×”):
√
√
√
√
×
腰
腰
三边都不相等的三角形
等腰三角形
等边三角形
也叫正三角形
底边
顶角
底角
底角
探
没有边相等
特殊
更特殊
两边相等
三边相等
一般
有两条边相等的三角形叫做等腰三角形.如图,在等腰三角形ABC中,AB=AC,它的各边与各角的名称如图所示.
三边都相等的三角形叫做等边三角形,也叫正三角形.
思考:你认为等边三角形与等腰三角形有什么关系?
把所有的三角形看作一个整体,三边都不相等的三角形、等腰三角形和等边三角形都是这个整体的一部分。画图表示它们之间的关系。
三角形
三边都不相等的三角形
等腰三角形
(两边相等)
底边和腰不相等的等腰三角形
等边三角形
特别提示:等边三角形是特殊的等腰三角形.是底边和腰相等的等腰三角形.
1、下列说法中正确的是( )
A、等腰三角形一定是等边三角形
B、由三条线段组成的图形叫做三角形
C、等边三角形是等腰三角形
D、三角形可分为不等边三角形和等边三角形
2、下列说法正确的是( )
A、一个钝角三角形一定不是等腰三角形。
B、一个等腰三角形一定是锐角三角形或直角三角形。
C、一个直角三角形一定不是等腰三角形,也不是直角三角形。
D、一个等边三角形一定不是钝角三角形,也不是直角三角形。
认识了三角形,知道了三角形的表示法。
知道三角形的构成。
掌握了三角形按角分类。
掌握了三角形按边分类。
测
一.选择题
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
2、下列说法中正确的有( )个
A、三角形按边分类可以分为等腰三角形、等边三角形和不等边三角形
B、三角形按角分类可以分为锐角三角形、直角三角形和钝角三角形。
C、一个三角形里面有两个锐角,则一定是锐角三角形。
D、所有的等腰三角形都是锐角三角形。
不以规矩,不能成方圆!
1、积极发言的同学
2、最优秀的小组
3、进步最大的同学
图片中有一种共同的平面图形,你发现了吗?
学习目标:
1、经历从具体情境中抽象出三角形建立几何模型的过程,能规范说出三角形的定义和构成。
2、能把三角形按一定的标准进行分类,培养不重不漏的分类思想。
活动二:归纳定义 规范表示
背景
定义、表示
划分(以角、边为标准)
性质(从角、边的角度研究)
特殊三角形(性质和判定)
应用
中学三角形的学习将从以下几个方面展开
本节目标
1、什么叫三角形?
怎么表示一个三角形?
2、什么叫三角形的边?
3、什么叫三角形的顶点?
4、什么叫三角形的角?
课本130页
三角形的构成
三角形
由不在同一条直线上的三条线段
首尾顺次相接所组成的图形。
三角形的边
组成三角形的线段
三角形的顶点
相邻两边的公共端点
A
B
C
三角形的内角
相邻两边所组成的角
学
如何表示一个三角形呢?
记法 : 三角形符号“△”
图中的三角形
记作:△ABC(△BCA、△CAB)
读作:“三角形ABC”
三个顶点:顶点A、顶点B、顶点C
三个内角:∠A、∠B、∠C
三条边:三边 AB(a)、BC(b)、AC(c)
如图,三角形ABC有几条边?它们分别是什么?
△ABC的三边,有时也用a、b、c来表示.一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
解:三条,它们分别是AB、AC、BC.
三角形的边
A
1、图中有 个三角形,并分别用字母表示出来 。
2、 ∠AED是 的角?
3、AE 和 的公共边?
4、 ∠D是 和 的公共角?
D
C
B
E
A
锐角三角形
直角三角形
钝角三角形
三角形
锐角三角形
直角三角形
钝角三角形
把所有的三角形看作一个整体,锐角三角形、直角三角形和钝角三角形都是这个整体的一部分。它们之间的关系,可以用下图表示。
直角三角形各边名称
如图所示:
直角三角形通常用符号
“Rt△”表示.如图所示
直角三角形记Rt△ABC.
在直角三角形中三边中,哪条边最长?为什么?
直角三角形的两个锐角互余。
符号语言:在Rt△ABC中, ∠ C= 90° ∠ A+ ∠ B= 90°
1、锐角三角形的三个内角都是锐角;( )
2、钝角三角形的三个内角都是钝角;( )
3、直角三角形的斜边大于任何一条直角边;( )
4、三角形中至少有两个锐角;( )
5、三角形的三个内角中,最多有一个是钝角。
( )
判断题(对的填“√”,错的填“×”):
√
√
√
√
×
腰
腰
三边都不相等的三角形
等腰三角形
等边三角形
也叫正三角形
底边
顶角
底角
底角
探
没有边相等
特殊
更特殊
两边相等
三边相等
一般
有两条边相等的三角形叫做等腰三角形.如图,在等腰三角形ABC中,AB=AC,它的各边与各角的名称如图所示.
三边都相等的三角形叫做等边三角形,也叫正三角形.
思考:你认为等边三角形与等腰三角形有什么关系?
把所有的三角形看作一个整体,三边都不相等的三角形、等腰三角形和等边三角形都是这个整体的一部分。画图表示它们之间的关系。
三角形
三边都不相等的三角形
等腰三角形
(两边相等)
底边和腰不相等的等腰三角形
等边三角形
特别提示:等边三角形是特殊的等腰三角形.是底边和腰相等的等腰三角形.
1、下列说法中正确的是( )
A、等腰三角形一定是等边三角形
B、由三条线段组成的图形叫做三角形
C、等边三角形是等腰三角形
D、三角形可分为不等边三角形和等边三角形
2、下列说法正确的是( )
A、一个钝角三角形一定不是等腰三角形。
B、一个等腰三角形一定是锐角三角形或直角三角形。
C、一个直角三角形一定不是等腰三角形,也不是直角三角形。
D、一个等边三角形一定不是钝角三角形,也不是直角三角形。
认识了三角形,知道了三角形的表示法。
知道三角形的构成。
掌握了三角形按角分类。
掌握了三角形按边分类。
测
一.选择题
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
2、下列说法中正确的有( )个
A、三角形按边分类可以分为等腰三角形、等边三角形和不等边三角形
B、三角形按角分类可以分为锐角三角形、直角三角形和钝角三角形。
C、一个三角形里面有两个锐角,则一定是锐角三角形。
D、所有的等腰三角形都是锐角三角形。
不以规矩,不能成方圆!
1、积极发言的同学
2、最优秀的小组
3、进步最大的同学
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
