高二数学(人教版)必修2课件:§3.1.2两条直线平行与垂直的判定(共23张PPT)
文档属性
| 名称 | 高二数学(人教版)必修2课件:§3.1.2两条直线平行与垂直的判定(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 412.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 09:00:31 | ||
图片预览







文档简介
(共23张PPT)
1、理解并掌握两条直线平行与垂直的条件;
2、会运用条件判定两直线是否平行或垂直.
学习目标
直线的倾斜角
斜率
斜率公式
定义
范围
复习回顾
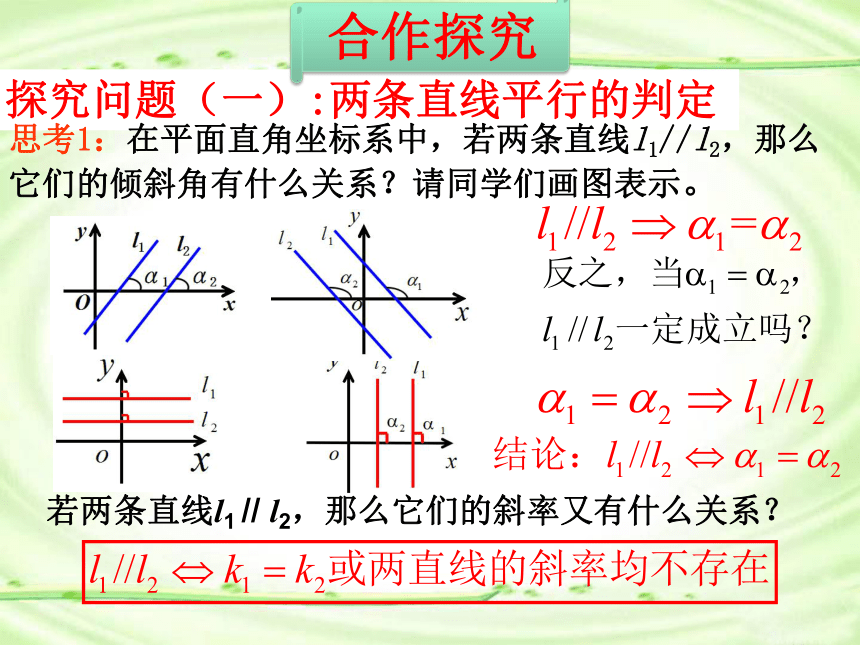
探究问题(一):两条直线平行的判定
思考1:在平面直角坐标系中,若两条直线l1//l2,那么它们的倾斜角有什么关系?请同学们画图表示。
若两条直线l1
//
l2,那么它们的斜率又有什么关系?
合作探究
(3)若两条不重合的直线的斜率都不存在,它们平行
。
(1)
若两条直线的斜率相等,这两条直线一定平行。
概念巩固
(2)若两条直线平行,则它们的斜率一定相等。
(×)
(×)
(√
)
注意重合
斜率不存在
(2)两条直线可能重合,斜率都存在
,则:
注意:
等价的前提是两直线斜率都存在
特殊情况下的两直线平行:
两直线斜率都不存在,两直线互相平行
结论1:(1)两条直线不重合,斜率都存在
,则:
[化解疑难]
对两直线平行与斜率的关系要注意以下几点
(1)l1∥l2 k1=k2成立的前提条件是:
①两条直线的斜率都存在;②l1与l2不重合.
(2)当两条直线不重合且斜率都不存在时,l1与l2的倾斜角都是90°,则l1∥l2.
(3)两条不重合直线平行的判定的一般结论是:
l1∥l2 k1=k2或l1,l2斜率都不存在.
例1.
已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
x
y
O
B
A
P
Q
解:
例题讲解
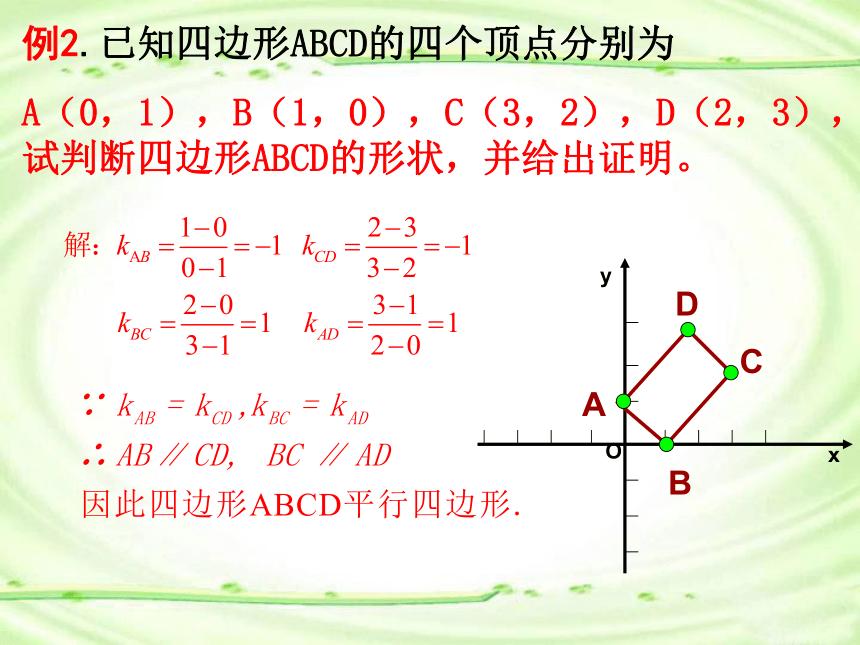
例2.已知四边形ABCD的四个顶点分别为
A(0,1),B(1,0),C(3,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
O
x
y
D
C
A
B
例2、已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
例题讲解
O
x
y
∥
∥
平行关系
A
B
C
D
问题探究二:两直线垂直,它们斜率有何关系?
填一填
已知两条直线l1和l2,其倾斜角分别为α1和α2(α1<α2),且l1⊥l2,如图所示,问:
α1与α2之间有什么关系呢?
-1
1
k1k2=
-1
,k1=
,k2=
;
,k1=
,k2=
.
,k1=
,k2=
.
α2=90°+α1
120°
135°
150°
你能发现k1与k2之间有什么关系吗?
O
x
l2
y
l1
α1
α2
设两条直线l
1、
l
2的倾斜角分别为α1、α2
(α1,α2≠
90°),且α1<α2,其斜率分别为k1,k2。(公式:
)
y
x
O
l2
l1
α1
α2
问题探究二:两直线垂直与它们斜率有何关系?
思考2
当k1k2=-1时,l1与l2的位置关系如何?
l1⊥l2
对于两条直线l1,
l2,其斜率分别
为
k1,k2
,则有
这个结论在图 中成立的吗?
k1·k2=-1或一条直线的斜率不存在,
同时另一条直线的斜率等于零.
结论:
它们的斜率互为负倒数
[类题通法]
使用斜率公式判定两直线垂直的步骤
(1)一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第一步.
(2)二用:就是将点的坐标代入斜率公式.
(3)求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式要对参数进行讨论.
总之,l1与l2一个斜率为0,另一个斜率不存在时,l1⊥l2;l1与l2斜率都存在时,满足k1·k2=-1.它们的斜率互为负倒数。
判断下列说法的对与错:
(1)
若两条直线的斜率之积等于-1,
这两条直线
一定垂直.
(
)
(2)
若两条直线垂直,
则它们的斜率之积一定为-1.
(
)
×
√
巩固练习
例3、已知A(-6,0),B(3,6),P(0,3)
Q(6,-6),判断直线AB与PQ的位置关系。
例题讲解
例3:
已知A(0,1),B(2,2),C(1,-1),
D(3,0),你能判断直线AB与CD,AB与AC的
位置关系吗?并证明你的结论。
A
B
C
D
例题讲解
例4、已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。
O
x
y
A
C
B
已知四边形ABCD的四个顶点分别为
A(0,1),B(1,0),C(3,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
O
x
y
D
C
A
B
变式:
1、已知过点A(-2,m)和B(m,4)的直线
与斜率为-2的直线平行,则m的值是(
)
A.-8
B.0
C.2
D.10
A
2、经过两点A(m,3)与B(2,2m)的直线
l与倾斜角为45 的直线互相垂直,则m的值
为
1
当堂检测
小结
:
2
1
l
l
和
结论1:对于两条不重合的直线
.
,
2
1
都不存在
或
k
k
l1∥l2
k1=k2.
条件:不重合、都有斜率
结论2:
:
2
1
l
l
和
对于任意两条直线
.
,
2
1
另一个不存在
中一个为0,
或
k
k
l1⊥l2
k1k2=-1.
条件:都有斜率
作用:根据斜率可证明三点共线、判断三角形或四边形的形状。
练习:
2、试确定m的值,使过点A(m,1),B(-1,m)
的直线与过点p(1,2),Q(-5,0)的直线
(1)平行;
(2)垂直。
课本P89练习T2
3:已知点A(m,1),B(-3,4),C(1,m),D(-1,m+1),分别在下列条件下求实数m的值:
(1)直线AB与CD平行;
(2)直线AB与CD垂直.
课本P90B组T2
(1)m=3
(1)m=-9/2
1、理解并掌握两条直线平行与垂直的条件;
2、会运用条件判定两直线是否平行或垂直.
学习目标
直线的倾斜角
斜率
斜率公式
定义
范围
复习回顾
探究问题(一):两条直线平行的判定
思考1:在平面直角坐标系中,若两条直线l1//l2,那么它们的倾斜角有什么关系?请同学们画图表示。
若两条直线l1
//
l2,那么它们的斜率又有什么关系?
合作探究
(3)若两条不重合的直线的斜率都不存在,它们平行
。
(1)
若两条直线的斜率相等,这两条直线一定平行。
概念巩固
(2)若两条直线平行,则它们的斜率一定相等。
(×)
(×)
(√
)
注意重合
斜率不存在
(2)两条直线可能重合,斜率都存在
,则:
注意:
等价的前提是两直线斜率都存在
特殊情况下的两直线平行:
两直线斜率都不存在,两直线互相平行
结论1:(1)两条直线不重合,斜率都存在
,则:
[化解疑难]
对两直线平行与斜率的关系要注意以下几点
(1)l1∥l2 k1=k2成立的前提条件是:
①两条直线的斜率都存在;②l1与l2不重合.
(2)当两条直线不重合且斜率都不存在时,l1与l2的倾斜角都是90°,则l1∥l2.
(3)两条不重合直线平行的判定的一般结论是:
l1∥l2 k1=k2或l1,l2斜率都不存在.
例1.
已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
x
y
O
B
A
P
Q
解:
例题讲解
例2.已知四边形ABCD的四个顶点分别为
A(0,1),B(1,0),C(3,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
O
x
y
D
C
A
B
例2、已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
例题讲解
O
x
y
∥
∥
平行关系
A
B
C
D
问题探究二:两直线垂直,它们斜率有何关系?
填一填
已知两条直线l1和l2,其倾斜角分别为α1和α2(α1<α2),且l1⊥l2,如图所示,问:
α1与α2之间有什么关系呢?
-1
1
k1k2=
-1
,k1=
,k2=
;
,k1=
,k2=
.
,k1=
,k2=
.
α2=90°+α1
120°
135°
150°
你能发现k1与k2之间有什么关系吗?
O
x
l2
y
l1
α1
α2
设两条直线l
1、
l
2的倾斜角分别为α1、α2
(α1,α2≠
90°),且α1<α2,其斜率分别为k1,k2。(公式:
)
y
x
O
l2
l1
α1
α2
问题探究二:两直线垂直与它们斜率有何关系?
思考2
当k1k2=-1时,l1与l2的位置关系如何?
l1⊥l2
对于两条直线l1,
l2,其斜率分别
为
k1,k2
,则有
这个结论在图 中成立的吗?
k1·k2=-1或一条直线的斜率不存在,
同时另一条直线的斜率等于零.
结论:
它们的斜率互为负倒数
[类题通法]
使用斜率公式判定两直线垂直的步骤
(1)一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第一步.
(2)二用:就是将点的坐标代入斜率公式.
(3)求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式要对参数进行讨论.
总之,l1与l2一个斜率为0,另一个斜率不存在时,l1⊥l2;l1与l2斜率都存在时,满足k1·k2=-1.它们的斜率互为负倒数。
判断下列说法的对与错:
(1)
若两条直线的斜率之积等于-1,
这两条直线
一定垂直.
(
)
(2)
若两条直线垂直,
则它们的斜率之积一定为-1.
(
)
×
√
巩固练习
例3、已知A(-6,0),B(3,6),P(0,3)
Q(6,-6),判断直线AB与PQ的位置关系。
例题讲解
例3:
已知A(0,1),B(2,2),C(1,-1),
D(3,0),你能判断直线AB与CD,AB与AC的
位置关系吗?并证明你的结论。
A
B
C
D
例题讲解
例4、已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。
O
x
y
A
C
B
已知四边形ABCD的四个顶点分别为
A(0,1),B(1,0),C(3,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
O
x
y
D
C
A
B
变式:
1、已知过点A(-2,m)和B(m,4)的直线
与斜率为-2的直线平行,则m的值是(
)
A.-8
B.0
C.2
D.10
A
2、经过两点A(m,3)与B(2,2m)的直线
l与倾斜角为45 的直线互相垂直,则m的值
为
1
当堂检测
小结
:
2
1
l
l
和
结论1:对于两条不重合的直线
.
,
2
1
都不存在
或
k
k
l1∥l2
k1=k2.
条件:不重合、都有斜率
结论2:
:
2
1
l
l
和
对于任意两条直线
.
,
2
1
另一个不存在
中一个为0,
或
k
k
l1⊥l2
k1k2=-1.
条件:都有斜率
作用:根据斜率可证明三点共线、判断三角形或四边形的形状。
练习:
2、试确定m的值,使过点A(m,1),B(-1,m)
的直线与过点p(1,2),Q(-5,0)的直线
(1)平行;
(2)垂直。
课本P89练习T2
3:已知点A(m,1),B(-3,4),C(1,m),D(-1,m+1),分别在下列条件下求实数m的值:
(1)直线AB与CD平行;
(2)直线AB与CD垂直.
课本P90B组T2
(1)m=3
(1)m=-9/2
同课章节目录
