高中数学人教A版必修2 课件:3.3.2-两点间的距离(共18张PPT)
文档属性
| 名称 | 高中数学人教A版必修2 课件:3.3.2-两点间的距离(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 773.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
1.理解两点间距离公式的推导方法,掌握此公式,并能用其解决实际问题
2.初步体会坐标法解决平面几何问题的思想,掌握运用坐标法证明简单平面几何问题的步骤
【预习导航】
1,平面内两点P1(x1,y1),P2(x2,y2)则
两点间的距离|P1
P2|=__________________
2,当
所在直线与y轴垂直时,
P1
、P2
3,当P1
、P2
所在直线与x轴垂直时,
4.原点与任一点P(x,y)的距离
P1
、P2
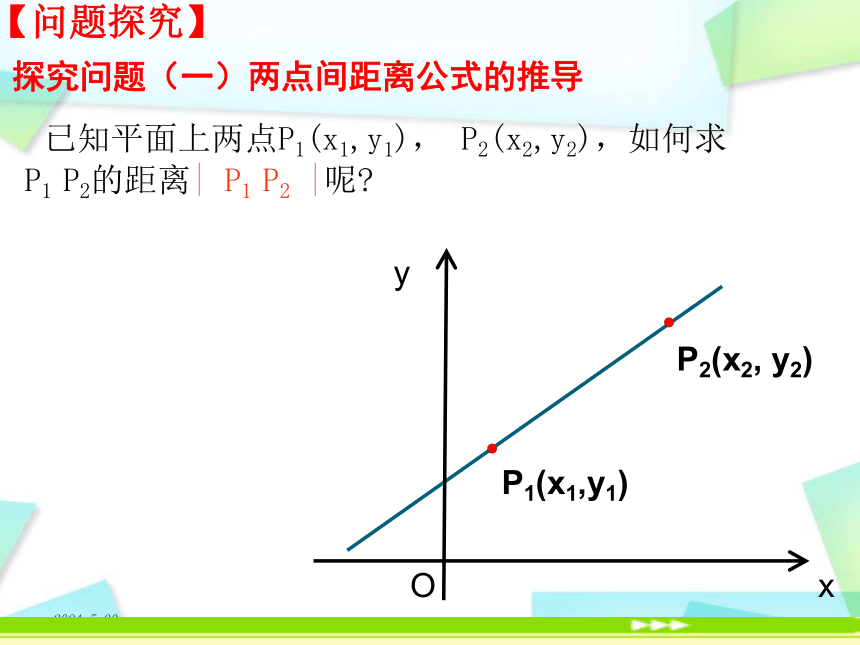
已知平面上两点P1(x1,y1),
P2(x2,y2),如何求P1
P2的距离|
P1
P2
|呢
探究问题(一)两点间距离公式的推导
【问题探究】
O
P1(x1,y1)
P2(x2,
y2)
y
x
已知:
和
,
x
o
y
1)、y1=y2
2)、x1=x2
x
o
y
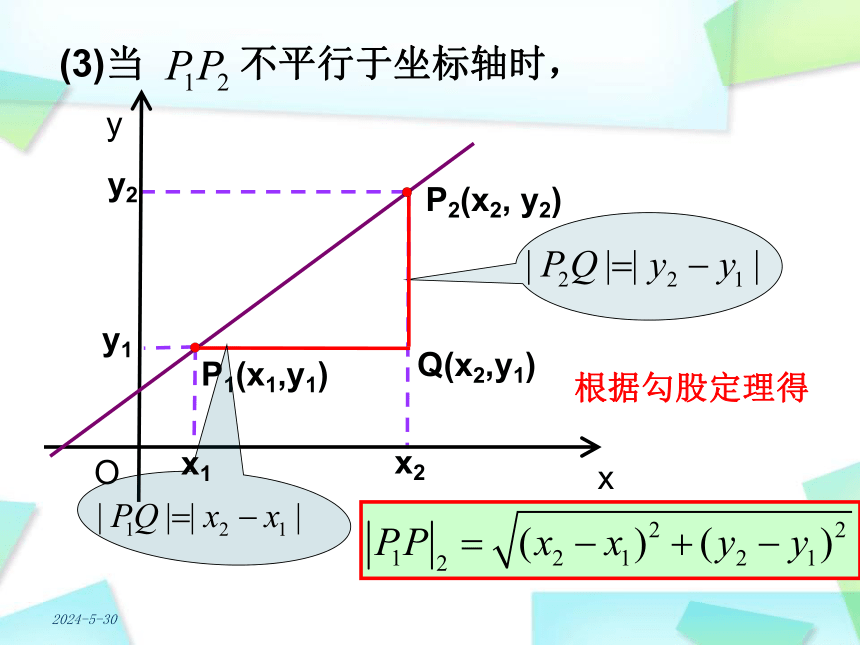
x
y
P1(x1,y1)
P2(x2,
y2)
Q(x2,y1)
O
x2
y2
x1
y1
(3)当
不平行于坐标轴时,
根据勾股定理得
特别地,点P(x,y)到原点(0,0)的距离为
一般地,已知平面上两点P1(x1,y1
)和P2(x2,y2),利用上述方法求点P1和P2的距离为
小结:两点间距离公式
注意公式的逆用
文字语言:横坐标之差的平方与纵坐标之差的平方和的算术平方根
例1、求下列两点间的距离:
(1)、A(6,0),B(-2,0)
(2)、C(0,-4),D(0,-1)
(3)、P(6,0),Q(0,-2)
(4)、M(2,1),N(5,-1)
解:
探究问题(二)两点间距离公式的运用
求点的坐标,一般就设其坐标
1、求在x轴上与点A(5,12)的距离为13的坐标;
2、已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标。
小试身手
(0,0)或(10,0)
y=-1,或y=11
3.已知
证明:以A为原点,AB为x轴建立直角坐标系.
探究问题(三)用两点间距离公式证明平面几何问题
例3
证明平行四边形四条边的平方和等于两条对角线的平方和.
x
y
A(0,0)
B(a,0)
C(a+b,c)
D
(b,c)
则四顶点坐标为A(0,0),B(a,0),D(b,c),C(a+b,c)
建立坐标系,
用坐标表示
有关的量。
y
x
o
A
B
D
C
(0,0)
(a,0)
(a+b,c)
(b,c)
练习1:证明直角三角形斜边上的中点到三个顶点的距离相等
[分析] 取直角边所在的直线为坐标轴建立坐标系,再写出各顶点坐标,给出证明.
[点评] 在建立坐标系时,适当的坐标系能使运算更加简便(如本例以两直角边为坐标轴建立坐标系),故在建坐标系时要有效地利用条件中的垂直、对称等关系.
即直角三角形斜边上的中点到三个顶点的距离相等
点评:
1.两点间的距离公式可用来解决一些有关距离的问题
(如根据各边长度判断三角形或四边形的形状),根据条件直接套用公式即可,要注意公式的变形应用,公式中两点的位置没有先后之分.
2.
应用坐标法解决平面几何问题的一般步骤是:
第一步:建立坐标系,建系时应使尽可能多的点落在坐标轴上,并且充分利用图形的对称性,用坐标
表示有关的量.
第二步:进行有关代数运算;
第三步:把代数运算结果“翻译”成几何关系.
注意逆用
平面内两点P1(x1,y1),
P2(x2,y2)
的距离公式是
【作业布置】
【课堂小结】
习题3.3
A组
6.
7.
8
1.理解两点间距离公式的推导方法,掌握此公式,并能用其解决实际问题
2.初步体会坐标法解决平面几何问题的思想,掌握运用坐标法证明简单平面几何问题的步骤
【预习导航】
1,平面内两点P1(x1,y1),P2(x2,y2)则
两点间的距离|P1
P2|=__________________
2,当
所在直线与y轴垂直时,
P1
、P2
3,当P1
、P2
所在直线与x轴垂直时,
4.原点与任一点P(x,y)的距离
P1
、P2
已知平面上两点P1(x1,y1),
P2(x2,y2),如何求P1
P2的距离|
P1
P2
|呢
探究问题(一)两点间距离公式的推导
【问题探究】
O
P1(x1,y1)
P2(x2,
y2)
y
x
已知:
和
,
x
o
y
1)、y1=y2
2)、x1=x2
x
o
y
x
y
P1(x1,y1)
P2(x2,
y2)
Q(x2,y1)
O
x2
y2
x1
y1
(3)当
不平行于坐标轴时,
根据勾股定理得
特别地,点P(x,y)到原点(0,0)的距离为
一般地,已知平面上两点P1(x1,y1
)和P2(x2,y2),利用上述方法求点P1和P2的距离为
小结:两点间距离公式
注意公式的逆用
文字语言:横坐标之差的平方与纵坐标之差的平方和的算术平方根
例1、求下列两点间的距离:
(1)、A(6,0),B(-2,0)
(2)、C(0,-4),D(0,-1)
(3)、P(6,0),Q(0,-2)
(4)、M(2,1),N(5,-1)
解:
探究问题(二)两点间距离公式的运用
求点的坐标,一般就设其坐标
1、求在x轴上与点A(5,12)的距离为13的坐标;
2、已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标。
小试身手
(0,0)或(10,0)
y=-1,或y=11
3.已知
证明:以A为原点,AB为x轴建立直角坐标系.
探究问题(三)用两点间距离公式证明平面几何问题
例3
证明平行四边形四条边的平方和等于两条对角线的平方和.
x
y
A(0,0)
B(a,0)
C(a+b,c)
D
(b,c)
则四顶点坐标为A(0,0),B(a,0),D(b,c),C(a+b,c)
建立坐标系,
用坐标表示
有关的量。
y
x
o
A
B
D
C
(0,0)
(a,0)
(a+b,c)
(b,c)
练习1:证明直角三角形斜边上的中点到三个顶点的距离相等
[分析] 取直角边所在的直线为坐标轴建立坐标系,再写出各顶点坐标,给出证明.
[点评] 在建立坐标系时,适当的坐标系能使运算更加简便(如本例以两直角边为坐标轴建立坐标系),故在建坐标系时要有效地利用条件中的垂直、对称等关系.
即直角三角形斜边上的中点到三个顶点的距离相等
点评:
1.两点间的距离公式可用来解决一些有关距离的问题
(如根据各边长度判断三角形或四边形的形状),根据条件直接套用公式即可,要注意公式的变形应用,公式中两点的位置没有先后之分.
2.
应用坐标法解决平面几何问题的一般步骤是:
第一步:建立坐标系,建系时应使尽可能多的点落在坐标轴上,并且充分利用图形的对称性,用坐标
表示有关的量.
第二步:进行有关代数运算;
第三步:把代数运算结果“翻译”成几何关系.
注意逆用
平面内两点P1(x1,y1),
P2(x2,y2)
的距离公式是
【作业布置】
【课堂小结】
习题3.3
A组
6.
7.
8
