高中数学人教A版必修2 2.2.3 直线与平面平行的性质--课件(共18张PPT)
文档属性
| 名称 | 高中数学人教A版必修2 2.2.3 直线与平面平行的性质--课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 359.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-23 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
直线与平面平行的性质
回顾旧知
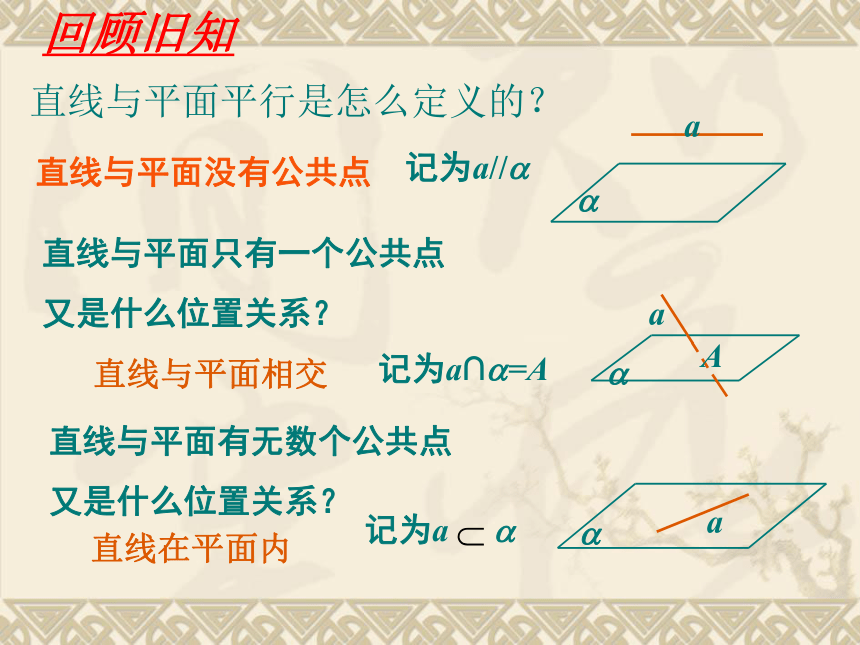
直线与平面只有一个公共点
又是什么位置关系?
直线与平面有无数个公共点
又是什么位置关系?
直线与平面平行是怎么定义的?
直线与平面没有公共点
a
记为a//
直线与平面相交
a
A
记为a∩ =A
直线在平面内
a
记为a
怎样判定一条直线和一个平面平行呢?
线面平行的定义
线面平行的判定定理
回顾旧知
直线与平面平行的判定定理
a
b
如果平面外一条直线与平面内的一条直线平行,
那么这条直线与这个平面平行.
(文字语言)
(符号语言)
(图形语言)
回顾旧知
C1
D1
实例引入
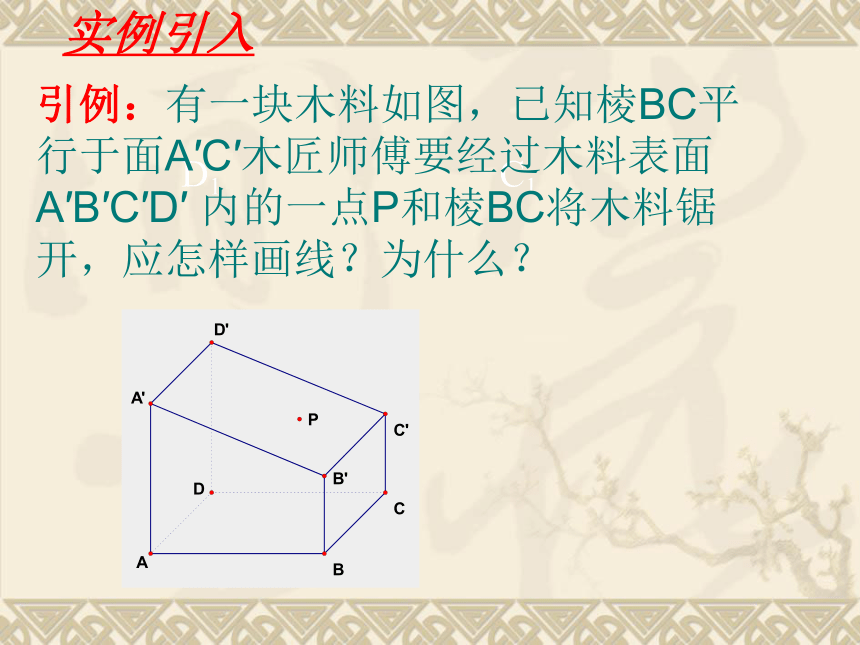
引例:有一块木料如图,已知棱BC平行于面A′C′木匠师傅要经过木料表面A′B′C′D′ 内的一点P和棱BC将木料锯开,应怎样画线?为什么?
问题探究
思辨论证
a
c
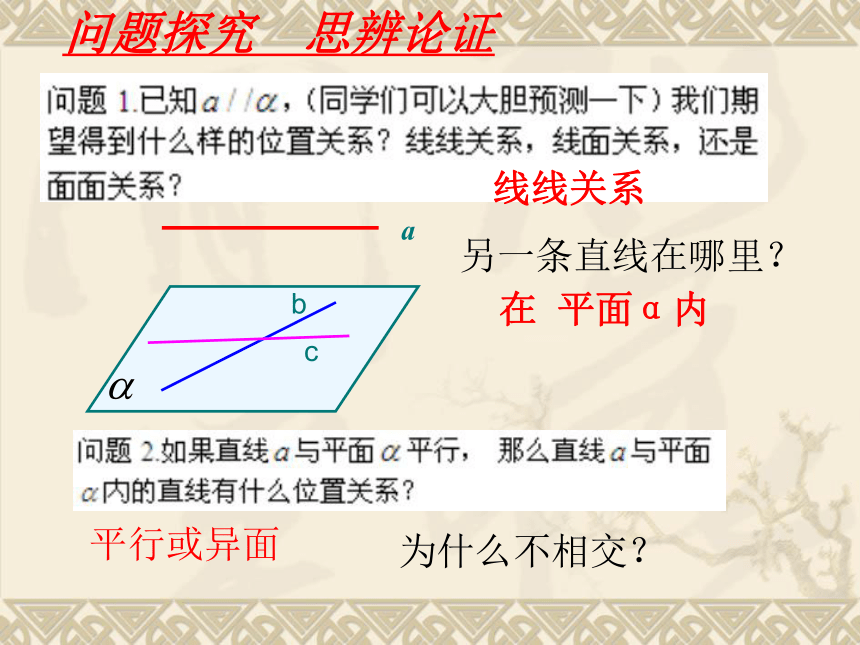
线线关系
另一条直线在哪里?
在
平面α内
平行或异面
为什么不相交?
b
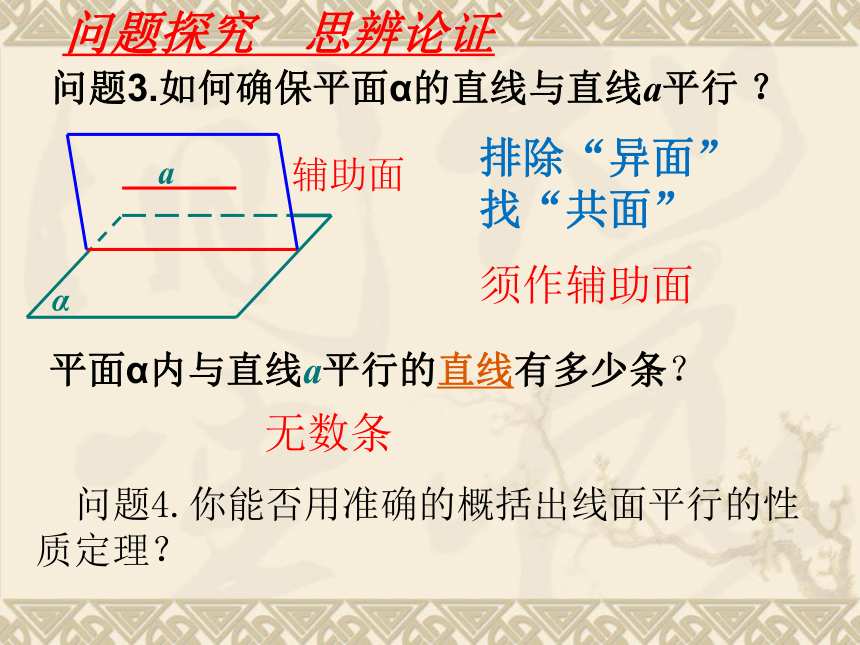
问题3.如何确保平面α的直线与直线a平行
?
排除“异面”
找“共面”
须作辅助面
问题探究
思辨论证
无数条
平面α内与直线a平行的直线有多少条?
α
a
辅助面
问题4.你能否用准确的概括出线面平行的性质定理?
α
β
b
a
如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行.
.
线面平行的性质定理
线线平行
线面平行
(转化)
(图形语言)
(文字语言)
(符号语言)
问题探究
思辨论证
已知:
求证:
.
.
α
β
b
a
如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行
问题探究
思辨论证
判定定理
线面平行
线线平行
性质定理
判定与性质对比
例1、一木匠手里有下图所示的一块木料(棱BC//面A
'
C
'
),
要经过面A
'
C
'内的一点P和棱BC将木料锯开,应怎样画线?为什么?
E
F
尝试应用
例1、一木匠手里有下图所示的一块木料(棱BC//面A
'
C
'
),
要经过面A
'
C
'内的一点P和棱BC将木料锯开,应怎样画线?为什么?
在平面A
'
C
'内,过点P画线段EF∥B
'
C
'
E
F
连接BE,CF,则EF,BE,CF就是应画的线,沿所画的线锯开即可。
由公理4得EF∥BC,则EF
与BC
共面。
尝试应用
例1、一木匠手里有下图所示的一块木料(棱BC//面A
'
C
'
),
要经过面A
'
C
'内的一点P和棱BC将木料锯开,应怎样画线?为什么?
在平面A
'
C
'内,过点P画线段EF∥B
'
C
'
E
F
连接BE,CF,则EF,BE,CF就是应画的线,沿所画的线锯开即可。
由公理4得EF∥BC,则EF
与BC
共面。
尝试应用
E
F
A′
D′
C′
B′
A
B
C
D
E
F
P
尝试应用
形成能力
例2.如图,求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
已知:
求证:
l
α
a
β
b
c
P
尝试应用
形成能力
证明:在平面α内取点P,使
过P和直线a作平面γ交α于
直线b
同理过a作平面δ交于β于直线c
同理
a//c
b//c
又
又
a//b
命题得证
a
α
a
γ
b
=
a
g
I
a//b
小结:关键是“作辅助面”
尝试应用
形成能力
线线平行
线面平行
平行线
定
判
理
定
定
理
性
质
辅助面
找
作
找
作
概括小结
提升思维
作业:
《直线与平面平行的性质》课时作业
直线与平面平行的性质
回顾旧知
直线与平面只有一个公共点
又是什么位置关系?
直线与平面有无数个公共点
又是什么位置关系?
直线与平面平行是怎么定义的?
直线与平面没有公共点
a
记为a//
直线与平面相交
a
A
记为a∩ =A
直线在平面内
a
记为a
怎样判定一条直线和一个平面平行呢?
线面平行的定义
线面平行的判定定理
回顾旧知
直线与平面平行的判定定理
a
b
如果平面外一条直线与平面内的一条直线平行,
那么这条直线与这个平面平行.
(文字语言)
(符号语言)
(图形语言)
回顾旧知
C1
D1
实例引入
引例:有一块木料如图,已知棱BC平行于面A′C′木匠师傅要经过木料表面A′B′C′D′ 内的一点P和棱BC将木料锯开,应怎样画线?为什么?
问题探究
思辨论证
a
c
线线关系
另一条直线在哪里?
在
平面α内
平行或异面
为什么不相交?
b
问题3.如何确保平面α的直线与直线a平行
?
排除“异面”
找“共面”
须作辅助面
问题探究
思辨论证
无数条
平面α内与直线a平行的直线有多少条?
α
a
辅助面
问题4.你能否用准确的概括出线面平行的性质定理?
α
β
b
a
如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行.
.
线面平行的性质定理
线线平行
线面平行
(转化)
(图形语言)
(文字语言)
(符号语言)
问题探究
思辨论证
已知:
求证:
.
.
α
β
b
a
如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行
问题探究
思辨论证
判定定理
线面平行
线线平行
性质定理
判定与性质对比
例1、一木匠手里有下图所示的一块木料(棱BC//面A
'
C
'
),
要经过面A
'
C
'内的一点P和棱BC将木料锯开,应怎样画线?为什么?
E
F
尝试应用
例1、一木匠手里有下图所示的一块木料(棱BC//面A
'
C
'
),
要经过面A
'
C
'内的一点P和棱BC将木料锯开,应怎样画线?为什么?
在平面A
'
C
'内,过点P画线段EF∥B
'
C
'
E
F
连接BE,CF,则EF,BE,CF就是应画的线,沿所画的线锯开即可。
由公理4得EF∥BC,则EF
与BC
共面。
尝试应用
例1、一木匠手里有下图所示的一块木料(棱BC//面A
'
C
'
),
要经过面A
'
C
'内的一点P和棱BC将木料锯开,应怎样画线?为什么?
在平面A
'
C
'内,过点P画线段EF∥B
'
C
'
E
F
连接BE,CF,则EF,BE,CF就是应画的线,沿所画的线锯开即可。
由公理4得EF∥BC,则EF
与BC
共面。
尝试应用
E
F
A′
D′
C′
B′
A
B
C
D
E
F
P
尝试应用
形成能力
例2.如图,求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
已知:
求证:
l
α
a
β
b
c
P
尝试应用
形成能力
证明:在平面α内取点P,使
过P和直线a作平面γ交α于
直线b
同理过a作平面δ交于β于直线c
同理
a//c
b//c
又
又
a//b
命题得证
a
α
a
γ
b
=
a
g
I
a//b
小结:关键是“作辅助面”
尝试应用
形成能力
线线平行
线面平行
平行线
定
判
理
定
定
理
性
质
辅助面
找
作
找
作
概括小结
提升思维
作业:
《直线与平面平行的性质》课时作业
