高中数学人教A版必修2 4.3.1 空间直角坐标系课件(共21张PPT)
文档属性
| 名称 | 高中数学人教A版必修2 4.3.1 空间直角坐标系课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 434.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
空间直角坐标系
x
O
数轴上的点可以用
唯一的一个实数表示
-1
-2
1
2
3
A
B
如何表示数轴上的点?
问题情境1
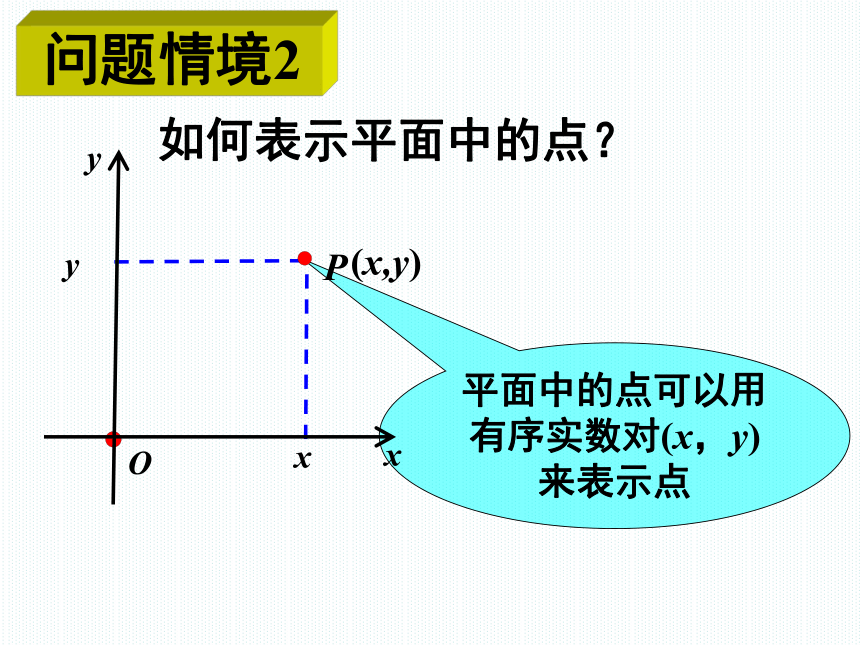
平面中的点可以用有序实数对(x,y)来表示点
x
y
P
O
x
y
(x,y)
如何表示平面中的点?
问题情境2
y
O
x
z
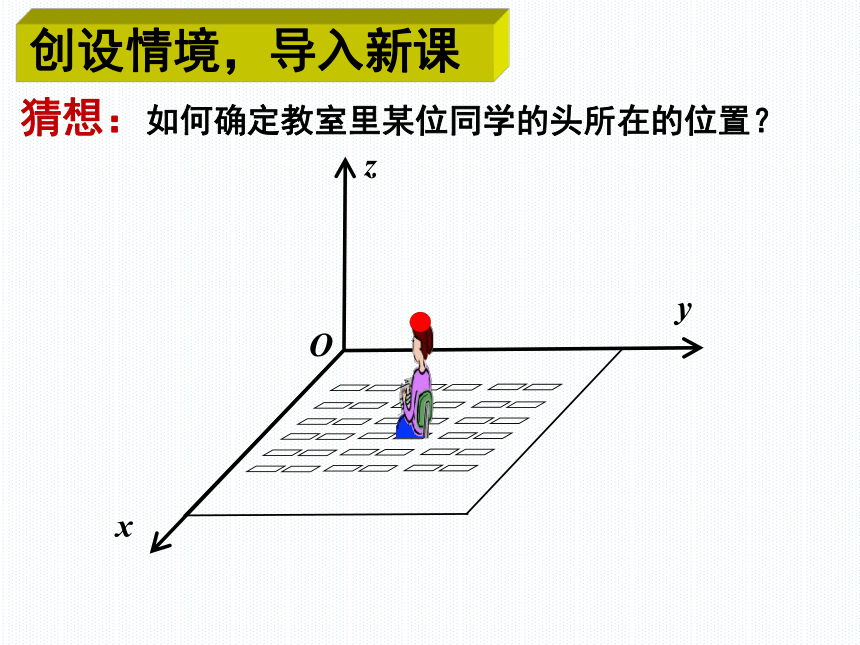
猜想:如何确定教室里某位同学的头所在的位置?
创设情境,导入新课
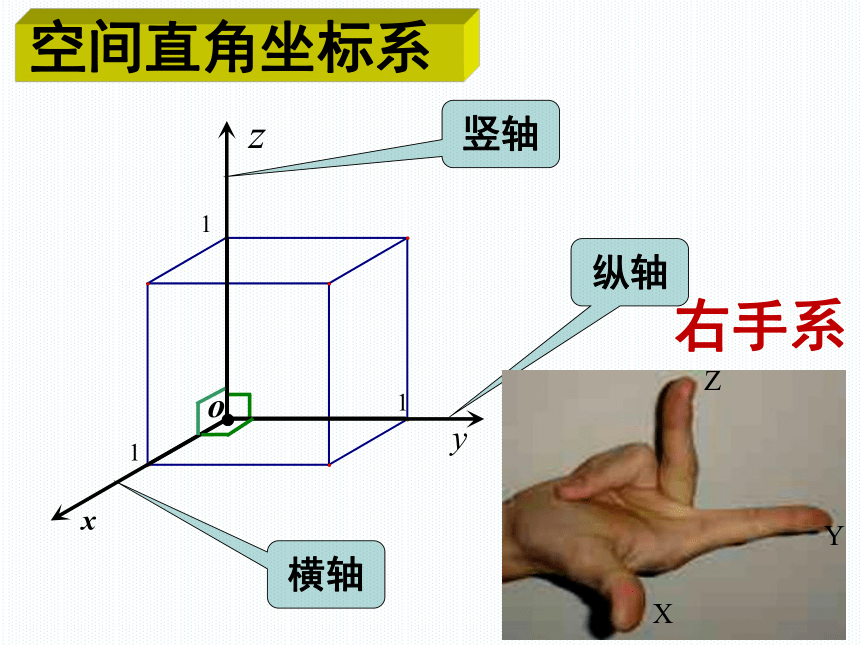
横轴
纵轴
竖轴
右手系
X
Y
Z
空间直角坐标系
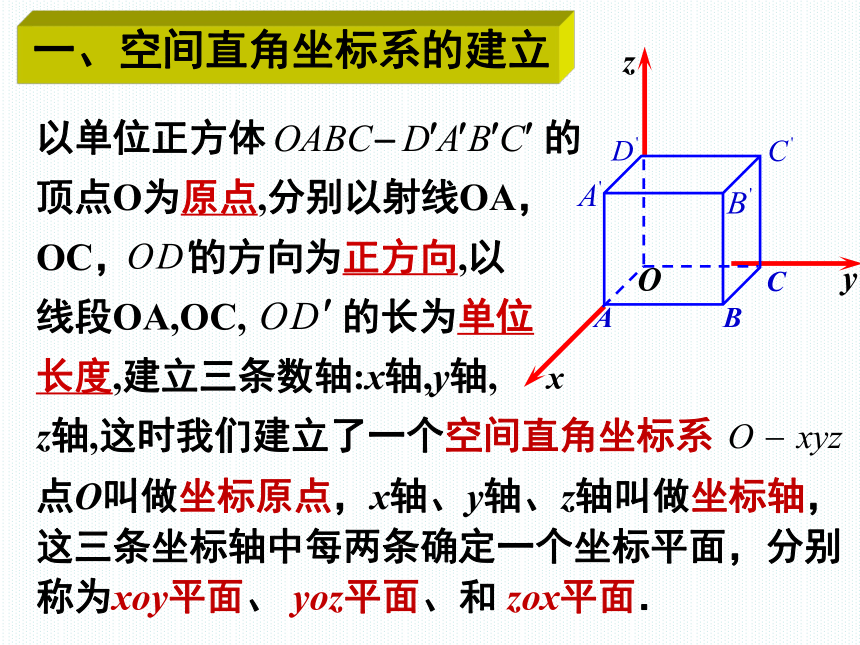
以单位正方体
的
顶点O为原点,分别以射线OA,
OC,
的方向为正方向,以
线段OA,OC,
的长为单位
长度,建立三条数轴:x轴,y轴,
z轴,这时我们建立了一个空间直角坐标系
y
x
z
A
B
C
O
点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、
yoz平面、和
zox平面.
一、空间直角坐标系的建立
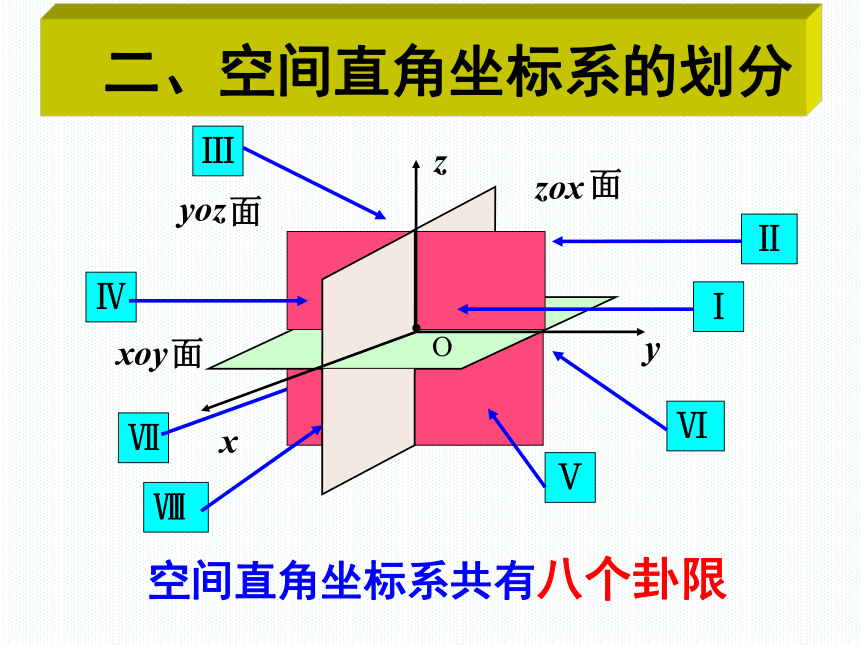
Ⅱ
Ⅶ
Ⅴ
Ⅵ
Ⅰ
Ⅲ
Ⅳ
Ⅷ
O
空间直角坐标系共有八个卦限
面
面
面
二、空间直角坐标系的划分
空间直角坐标系中任意一点的位置如何表示?
探究:
x称为点P的横坐标
O
x
y
z
Px
Pz
x
z
y
P
Py
y称为点P的纵坐标
z称为点P的竖坐标
反之:
(x,y,z)对应唯一的点P
空间的点P
有序数组
三、空间中点的坐标
空间中点的表示(方法二)
x
y
z
y
x
z
A
B
C
O
四棱柱
是单位正方体.如图建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标。
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
跟踪训练
规律:不见的那个就为“0”
O
x
y
z
1
1
1
A
D
C
B
E
F
点P的位置
原点O
x轴上A
y轴上B
z轴上C
坐标形式
点P的位置
xOy面内D
yOz面内E
zOx面内F
坐标形式
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
四、特殊位置的点的坐标:
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
(1)坐标平面内的点:
(2)坐标轴上的点:
O
x
y
z
1
1
1
A
D
C
B
E
F
规律总结:
规律:不见的那个就为“0”
应用举例
x
y
O
x0
y0
(x0,y0)
P
(x0
,
-y0)
P1
横坐标不变,
纵坐标相反。
(-x0
,y0)
P2
横坐标相反,
纵坐标不变。
P3
横坐标相反,
纵坐标相反。
-y0
-x0
(-x0
,
-y0)
关于谁对称谁不变
五、空间点的对称问题
类比探究1:
点M(x,y,z)是空间直角坐标系O-xyz中的一点
(1)与点M关于x轴对称的点:
(2)与点M关于y轴对称的点:
(3)与点M关于z轴对称的点:
(4)与点M关于原点对称的点:
(x,-y,-z)
(-x,y,-z)
(-x,-y,z)
(-x,-y,-z)
规律:见到谁谁不变,见不到变为相反数
五、空间点的对称问题
类比探究2:
点M(x,y,z)是空间直角坐标系O-xyz中的一点
(5)与点M关于平面xOy的对称点:
(x,y,-z)
(-x,y,z)
(x,-y,z)
(6)与点M关于平面yOz的对称点:
(7)与点M关于平面zOx的对称点:
五、空间点的对称问题
规律:见到谁谁不变,见不到变为相反数
1、空间直角坐标系的建立(三步)
2、空间直角坐标系的划分(八个卦限)
3、空间中点的坐标(一一对应)
4、特殊位置的点的坐标(表格)
5、空间点的对称问题
思想方法:数形结合、类比、化归
课堂小结:
空间直角坐标系
x
O
数轴上的点可以用
唯一的一个实数表示
-1
-2
1
2
3
A
B
如何表示数轴上的点?
问题情境1
平面中的点可以用有序实数对(x,y)来表示点
x
y
P
O
x
y
(x,y)
如何表示平面中的点?
问题情境2
y
O
x
z
猜想:如何确定教室里某位同学的头所在的位置?
创设情境,导入新课
横轴
纵轴
竖轴
右手系
X
Y
Z
空间直角坐标系
以单位正方体
的
顶点O为原点,分别以射线OA,
OC,
的方向为正方向,以
线段OA,OC,
的长为单位
长度,建立三条数轴:x轴,y轴,
z轴,这时我们建立了一个空间直角坐标系
y
x
z
A
B
C
O
点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、
yoz平面、和
zox平面.
一、空间直角坐标系的建立
Ⅱ
Ⅶ
Ⅴ
Ⅵ
Ⅰ
Ⅲ
Ⅳ
Ⅷ
O
空间直角坐标系共有八个卦限
面
面
面
二、空间直角坐标系的划分
空间直角坐标系中任意一点的位置如何表示?
探究:
x称为点P的横坐标
O
x
y
z
Px
Pz
x
z
y
P
Py
y称为点P的纵坐标
z称为点P的竖坐标
反之:
(x,y,z)对应唯一的点P
空间的点P
有序数组
三、空间中点的坐标
空间中点的表示(方法二)
x
y
z
y
x
z
A
B
C
O
四棱柱
是单位正方体.如图建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标。
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
跟踪训练
规律:不见的那个就为“0”
O
x
y
z
1
1
1
A
D
C
B
E
F
点P的位置
原点O
x轴上A
y轴上B
z轴上C
坐标形式
点P的位置
xOy面内D
yOz面内E
zOx面内F
坐标形式
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
四、特殊位置的点的坐标:
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
(1)坐标平面内的点:
(2)坐标轴上的点:
O
x
y
z
1
1
1
A
D
C
B
E
F
规律总结:
规律:不见的那个就为“0”
应用举例
x
y
O
x0
y0
(x0,y0)
P
(x0
,
-y0)
P1
横坐标不变,
纵坐标相反。
(-x0
,y0)
P2
横坐标相反,
纵坐标不变。
P3
横坐标相反,
纵坐标相反。
-y0
-x0
(-x0
,
-y0)
关于谁对称谁不变
五、空间点的对称问题
类比探究1:
点M(x,y,z)是空间直角坐标系O-xyz中的一点
(1)与点M关于x轴对称的点:
(2)与点M关于y轴对称的点:
(3)与点M关于z轴对称的点:
(4)与点M关于原点对称的点:
(x,-y,-z)
(-x,y,-z)
(-x,-y,z)
(-x,-y,-z)
规律:见到谁谁不变,见不到变为相反数
五、空间点的对称问题
类比探究2:
点M(x,y,z)是空间直角坐标系O-xyz中的一点
(5)与点M关于平面xOy的对称点:
(x,y,-z)
(-x,y,z)
(x,-y,z)
(6)与点M关于平面yOz的对称点:
(7)与点M关于平面zOx的对称点:
五、空间点的对称问题
规律:见到谁谁不变,见不到变为相反数
1、空间直角坐标系的建立(三步)
2、空间直角坐标系的划分(八个卦限)
3、空间中点的坐标(一一对应)
4、特殊位置的点的坐标(表格)
5、空间点的对称问题
思想方法:数形结合、类比、化归
课堂小结:
