2020年春人教版数学八年级下册第二十章 数据的分析 章末小结 习题课件(24张PPT)
文档属性
| 名称 | 2020年春人教版数学八年级下册第二十章 数据的分析 章末小结 习题课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第二十章
数据的分析
2
1
专题解读
……………..…
知识网络
……………..…
章末小结
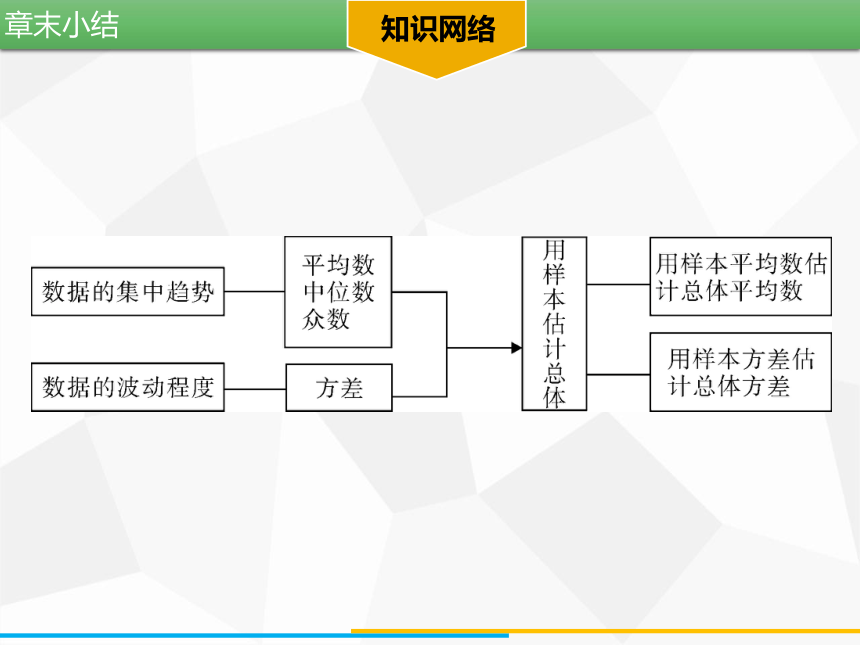
知识网络
专题解读
专题一:平均数
【例1】在一次数学测试中,某小组10名同学的成绩如下:1人100分,3人92分,3人80分,2人75分,1人54分.问:这小组数学成绩的平均分是多少?
【答案】解:
=82
答:这小组的数学成绩的平均分为82分.
【解析】直接运用加权平均数公式计算即可.
【点拔】在求一组数据的加权平均数时,要注意数据的权重.
专题解读
2.某次歌咏比赛中,选手张华的唱功、音乐常识、综
合知识分别得了90分,80分,85分,若这三项按
5∶3∶2的比例计算平均分,则张华的平均分是___
_________.
1.一组数据有5个3,7个5,8个9,这组数据的平均
数是__________.
86
6.1
专题解读
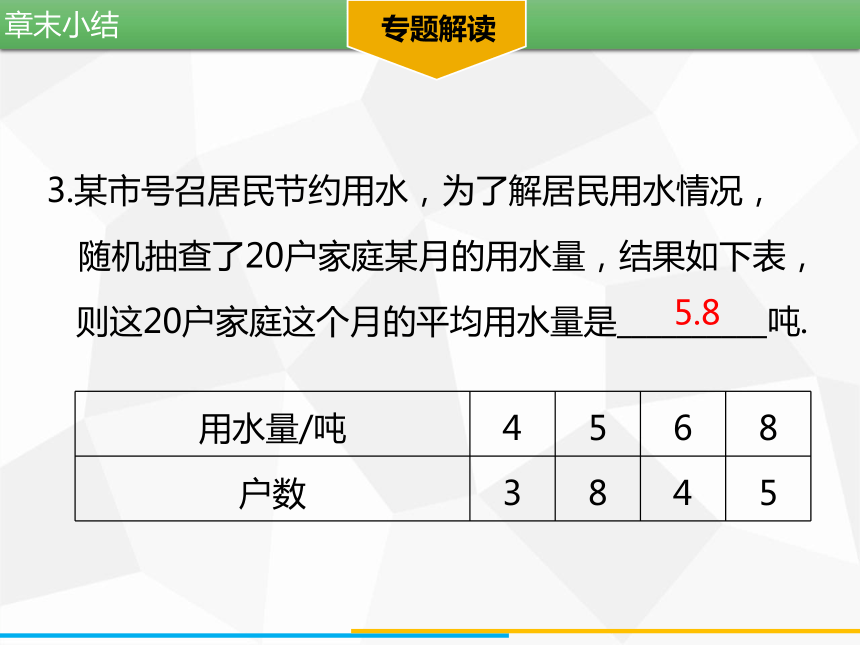
3.某市号召居民节约用水,为了解居民用水情况,
随机抽查了20户家庭某月的用水量,结果如下表,
则这20户家庭这个月的平均用水量是__________吨.
用水量/吨
4
5
6
8
户数
3
8
4
5
5.8
专题解读
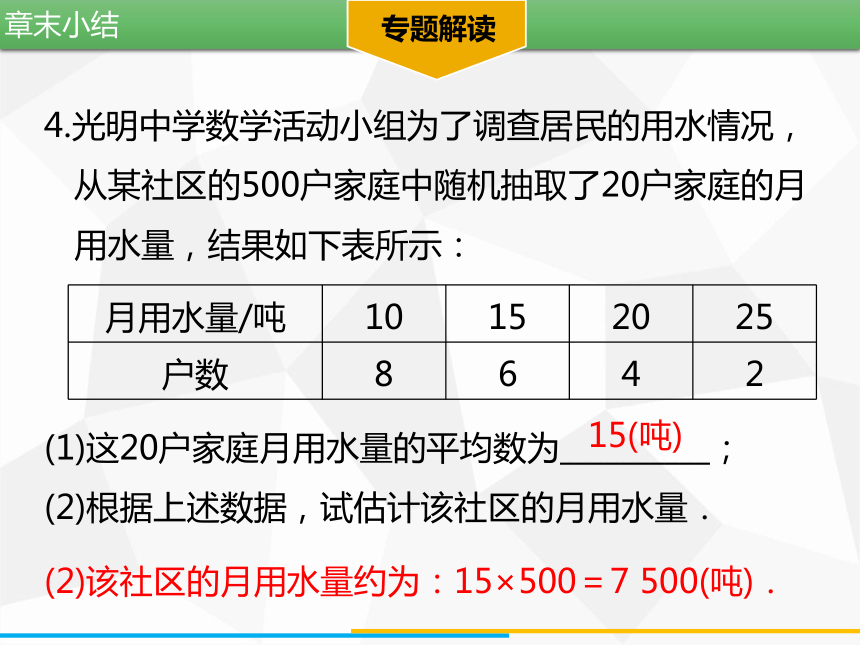
4.光明中学数学活动小组为了调查居民的用水情况,
从某社区的500户家庭中随机抽取了20户家庭的月
用水量,结果如下表所示:
(1)这20户家庭月用水量的平均数为__________;
(2)根据上述数据,试估计该社区的月用水量.
月用水量/吨
10
15
20
25
户数
8
6
4
2
15(吨)
(2)该社区的月用水量约为:15×500=7
500(吨).
专题解读
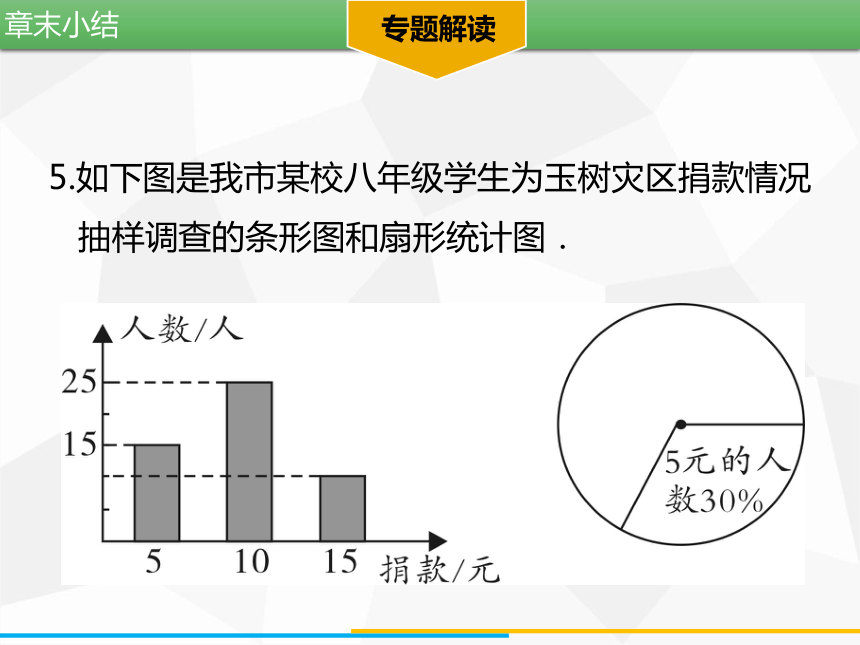
5.如下图是我市某校八年级学生为玉树灾区捐款情况
抽样调查的条形图和扇形统计图.
专题解读
(1)该样本的容量为__________;
(2)在扇形统计图中,该样本中捐款5元的圆心角度
数为________________________;
(3)若该校八年级学生有800人,据此样本求八年级
捐款总数.
30%×360°=108°
50
×800=7
600(元)
专题解读
专题二:中位数和众数
【例2】一支篮球队准备购买10双运动鞋,各种尺码统计如下表:
则这10双运动鞋尺码的众数是________,中位数是
__________.
尺码/厘米v
25
25.5
26
26.5
27
购买量/双
1
1
2
4
2
26.5
26.5
专题解读
【答案】26.5,26.5.
【解析】这组数据按照从小到大的顺序排列为:25,25.5,26,26,26.5,26.5,26.5,26.5,27,27;则众数为26.5,中位数为:(26.5+26.5)÷2=26.5
【点拔】注意中位数的求法,根据数据的个数分两种情况.
专题解读
专题训练二
6.2019年6月份,某市一周空气质量报告中某项
污染指数的数据是:31,35,31,32,30,
32,31.这组数据的众数为__________;中位数
为__________.
31
31
专题解读
7.在一次捐款中,某班第一组有10名同学,其捐款
数额统计如下表:
则捐款数额组成的一组数据中,众数是________,
中位数是__________.
捐款/元
10
15
20
50
人数
1
4
3
2
17.5
15
专题解读
8.某电脑公司的李经理对2018年9月份电脑的销
售情况做了调查,情况如下表:
每台价格/元
6
000
4
500
3
800
3
000
销量/台
20
40
60
30
专题解读
请你回答下列问题:
(1)2018年9月份电脑价格组成的数据平均数为
_________元,中位数为__________元;
(2)本月平均每天销售__________台(9月份为30天);
(3)如果你是该商场的经理,根据以上信息,应该
如何组织货源,并说明你的理由.
如:多进3
800元的电脑,适量
进些其他价位的电脑等;
4
120
3
800
5
专题解读
专题三:方差
【例3】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,10,7,8;
乙:9,5,10,9,7.
(1)将下表填写完整;
(2)若你是教练,根据以上信息,你会选择谁参加射击比
赛,理由是什么?
比较
平均数
方差
甲
乙
3.2
1.2
8
8
专题解读
【答案】(1)甲的平均数是8环,乙的平均数是8环,甲的方差是1.2.
(2)选择甲参加射击比赛,原因是甲乙两人的平均数一样,甲的方差比较小,根据方差越小成绩越稳定,因此甲成绩比较稳定,所以选择甲.
专题解读
【解析】(1)根据平均数的计算公式代值计算求出甲与乙的平均数,再根据方差的计算公式求出甲的方差;(2)根据甲乙的平均数、方差,在平均数相同的情况下,选择方差较小的即可.
【点拔】用方差的大小可以衡量甲、乙两个成绩的稳定性,方差越小,成绩越稳定.
专题解读
队员
第一次
第二次
第三次
第四次
第五次
第六次
甲
9
7
10
10
9
9
乙
10
8
9
8
10
9
9.省射击队为从甲、乙两名运动员中选拔一人参加全
国比赛,对他们进行了六次测试,成绩如下表(单
位:环)
专题解读
(1)根据表格中的数据,计算出甲的平均成绩是
__________环,乙的平均成绩是__________环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)你认为推荐谁参加全国比赛更合适,说明理由.
9
9
(2)S2甲=
1,
S2乙=
(3)选乙,因为甲乙两人平均数相同,
且乙的方差小,成绩比较稳定.
专题解读
10.某中学开展“唱红歌”比赛活动,九年级(1)、(2)
班根据初赛成绩,各选出5名选手参加复赛,两
个班各选出的5名选手的复赛成绩(满分为100分)
如下图所示.
专题解读
(1)根据图示填写下表;
班级
平均数/分
中位数/分
众数/分
九(1)
85
85
九(2)
80
100
85
85
专题解读
(2)结合两班复赛成绩的平均数和中位数,分析哪个
班级的复赛成绩较好;
(2)九(1)班成绩好些,因为两个班级的平均数相同,
九(1)班的中位数高,所以在平均数相同的情况下
中位数高的九(1)班成绩好些;
(3)计算两班复赛成绩的方差.
(3)S=70,S=160.
感谢聆听
第二十章
数据的分析
2
1
专题解读
……………..…
知识网络
……………..…
章末小结
知识网络
专题解读
专题一:平均数
【例1】在一次数学测试中,某小组10名同学的成绩如下:1人100分,3人92分,3人80分,2人75分,1人54分.问:这小组数学成绩的平均分是多少?
【答案】解:
=82
答:这小组的数学成绩的平均分为82分.
【解析】直接运用加权平均数公式计算即可.
【点拔】在求一组数据的加权平均数时,要注意数据的权重.
专题解读
2.某次歌咏比赛中,选手张华的唱功、音乐常识、综
合知识分别得了90分,80分,85分,若这三项按
5∶3∶2的比例计算平均分,则张华的平均分是___
_________.
1.一组数据有5个3,7个5,8个9,这组数据的平均
数是__________.
86
6.1
专题解读
3.某市号召居民节约用水,为了解居民用水情况,
随机抽查了20户家庭某月的用水量,结果如下表,
则这20户家庭这个月的平均用水量是__________吨.
用水量/吨
4
5
6
8
户数
3
8
4
5
5.8
专题解读
4.光明中学数学活动小组为了调查居民的用水情况,
从某社区的500户家庭中随机抽取了20户家庭的月
用水量,结果如下表所示:
(1)这20户家庭月用水量的平均数为__________;
(2)根据上述数据,试估计该社区的月用水量.
月用水量/吨
10
15
20
25
户数
8
6
4
2
15(吨)
(2)该社区的月用水量约为:15×500=7
500(吨).
专题解读
5.如下图是我市某校八年级学生为玉树灾区捐款情况
抽样调查的条形图和扇形统计图.
专题解读
(1)该样本的容量为__________;
(2)在扇形统计图中,该样本中捐款5元的圆心角度
数为________________________;
(3)若该校八年级学生有800人,据此样本求八年级
捐款总数.
30%×360°=108°
50
×800=7
600(元)
专题解读
专题二:中位数和众数
【例2】一支篮球队准备购买10双运动鞋,各种尺码统计如下表:
则这10双运动鞋尺码的众数是________,中位数是
__________.
尺码/厘米v
25
25.5
26
26.5
27
购买量/双
1
1
2
4
2
26.5
26.5
专题解读
【答案】26.5,26.5.
【解析】这组数据按照从小到大的顺序排列为:25,25.5,26,26,26.5,26.5,26.5,26.5,27,27;则众数为26.5,中位数为:(26.5+26.5)÷2=26.5
【点拔】注意中位数的求法,根据数据的个数分两种情况.
专题解读
专题训练二
6.2019年6月份,某市一周空气质量报告中某项
污染指数的数据是:31,35,31,32,30,
32,31.这组数据的众数为__________;中位数
为__________.
31
31
专题解读
7.在一次捐款中,某班第一组有10名同学,其捐款
数额统计如下表:
则捐款数额组成的一组数据中,众数是________,
中位数是__________.
捐款/元
10
15
20
50
人数
1
4
3
2
17.5
15
专题解读
8.某电脑公司的李经理对2018年9月份电脑的销
售情况做了调查,情况如下表:
每台价格/元
6
000
4
500
3
800
3
000
销量/台
20
40
60
30
专题解读
请你回答下列问题:
(1)2018年9月份电脑价格组成的数据平均数为
_________元,中位数为__________元;
(2)本月平均每天销售__________台(9月份为30天);
(3)如果你是该商场的经理,根据以上信息,应该
如何组织货源,并说明你的理由.
如:多进3
800元的电脑,适量
进些其他价位的电脑等;
4
120
3
800
5
专题解读
专题三:方差
【例3】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,10,7,8;
乙:9,5,10,9,7.
(1)将下表填写完整;
(2)若你是教练,根据以上信息,你会选择谁参加射击比
赛,理由是什么?
比较
平均数
方差
甲
乙
3.2
1.2
8
8
专题解读
【答案】(1)甲的平均数是8环,乙的平均数是8环,甲的方差是1.2.
(2)选择甲参加射击比赛,原因是甲乙两人的平均数一样,甲的方差比较小,根据方差越小成绩越稳定,因此甲成绩比较稳定,所以选择甲.
专题解读
【解析】(1)根据平均数的计算公式代值计算求出甲与乙的平均数,再根据方差的计算公式求出甲的方差;(2)根据甲乙的平均数、方差,在平均数相同的情况下,选择方差较小的即可.
【点拔】用方差的大小可以衡量甲、乙两个成绩的稳定性,方差越小,成绩越稳定.
专题解读
队员
第一次
第二次
第三次
第四次
第五次
第六次
甲
9
7
10
10
9
9
乙
10
8
9
8
10
9
9.省射击队为从甲、乙两名运动员中选拔一人参加全
国比赛,对他们进行了六次测试,成绩如下表(单
位:环)
专题解读
(1)根据表格中的数据,计算出甲的平均成绩是
__________环,乙的平均成绩是__________环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)你认为推荐谁参加全国比赛更合适,说明理由.
9
9
(2)S2甲=
1,
S2乙=
(3)选乙,因为甲乙两人平均数相同,
且乙的方差小,成绩比较稳定.
专题解读
10.某中学开展“唱红歌”比赛活动,九年级(1)、(2)
班根据初赛成绩,各选出5名选手参加复赛,两
个班各选出的5名选手的复赛成绩(满分为100分)
如下图所示.
专题解读
(1)根据图示填写下表;
班级
平均数/分
中位数/分
众数/分
九(1)
85
85
九(2)
80
100
85
85
专题解读
(2)结合两班复赛成绩的平均数和中位数,分析哪个
班级的复赛成绩较好;
(2)九(1)班成绩好些,因为两个班级的平均数相同,
九(1)班的中位数高,所以在平均数相同的情况下
中位数高的九(1)班成绩好些;
(3)计算两班复赛成绩的方差.
(3)S=70,S=160.
感谢聆听
