沪科版八年级数学下册课件:18.1勾股定理的应用(第二课时)(共28张PPT)
文档属性
| 名称 | 沪科版八年级数学下册课件:18.1勾股定理的应用(第二课时)(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 620.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 00:00:00 | ||
图片预览

文档简介
(共28张PPT)
第2课时 勾股定理的应用
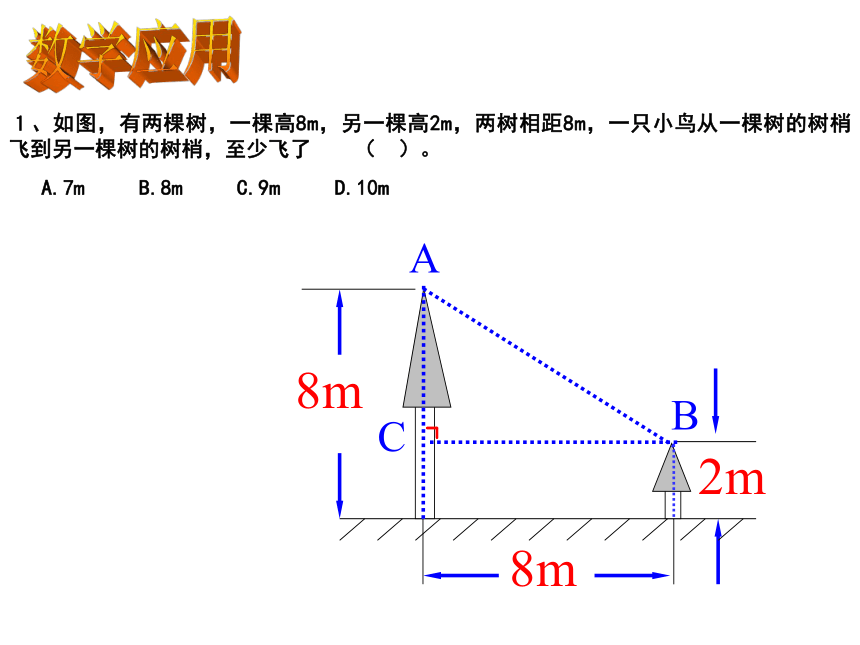
1、如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )。
A.7m B.8m C.9m D.10m
8m
2m
8m
·
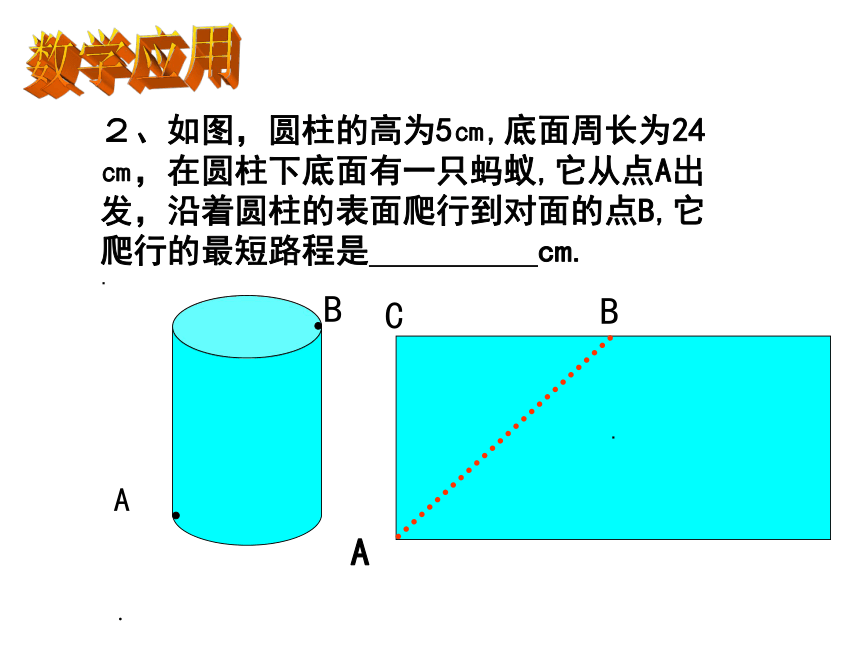
2、如图,圆柱的高为5㎝,底面周长为24㎝,在圆柱下底面有一只蚂蚁,它从点A出发,沿着圆柱的表面爬行到对面的点B,它爬行的最短路程是 cm.
·
·
A
B
C
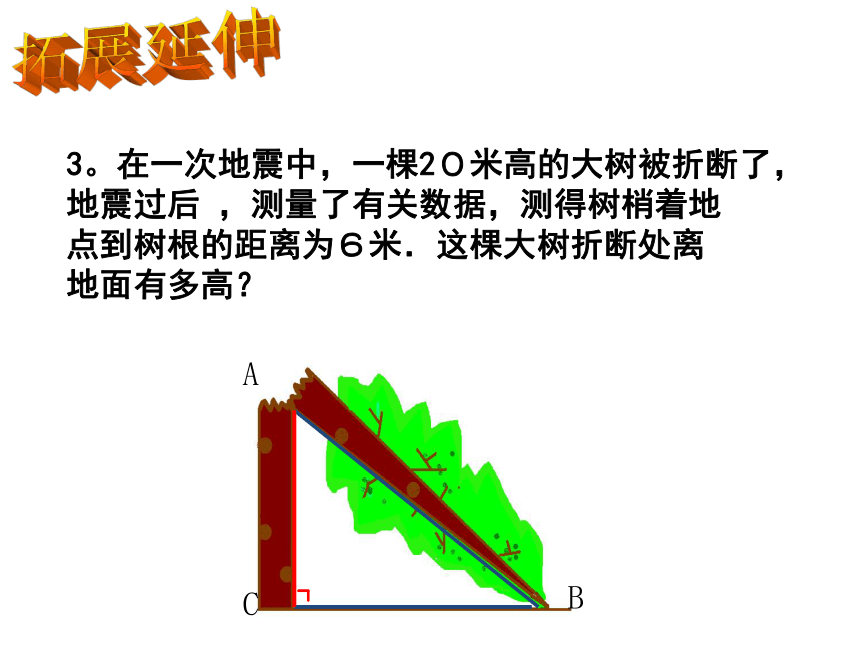
3。在一次地震中,一棵20米高的大树被折断了,
地震过后 ,测量了有关数据,测得树梢着地
点到树根的距离为6米.这棵大树折断处离
地面有多高?
B
第2课时 勾股定理的应用
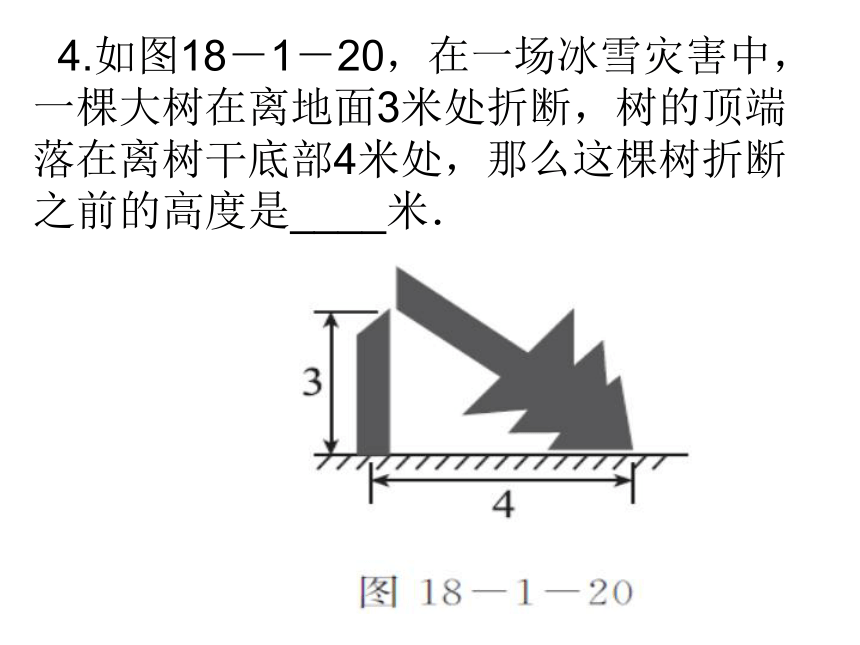
4.如图18-1-20,在一场冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是____米.
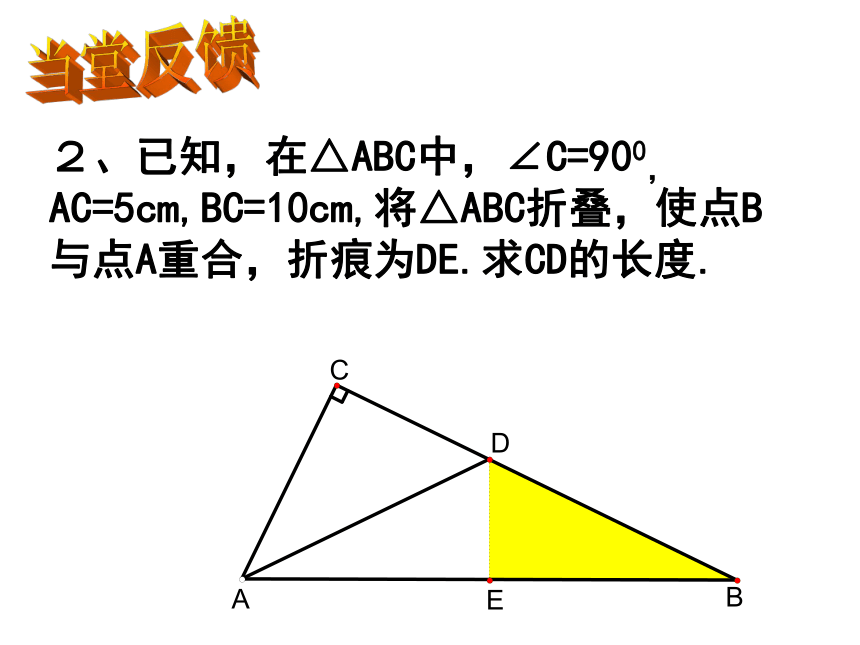
2、已知,在△ABC中,∠C=900,
AC=5cm,BC=10cm,将△ABC折叠,使点B
与点A重合,折痕为DE.求CD的长度.
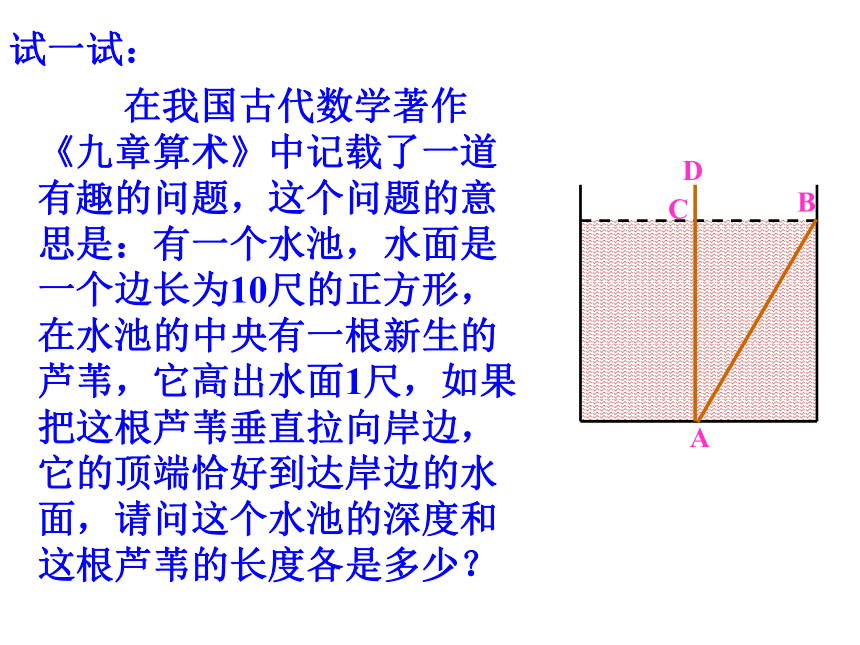
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
z
x
y
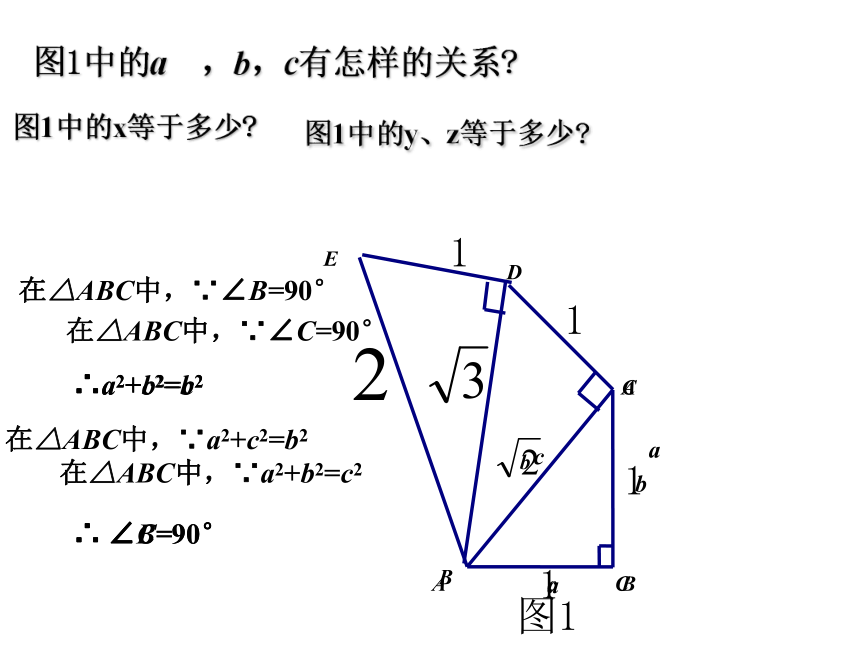
图1中的x等于多少?
图1中的y、z等于多少?
1
1
1
1
图1
A
B
C
D
E
a
b
c
A
B
C
b
a
c
图1中的a ,b,c有怎样的关系?
∴a2+b2=c2
在△ABC中,∵∠C=90°
∴ ∠C=90°
在△ABC中,∵a2+b2=c2
在△ABC中,∵∠B=90°
∴a2+c2=b2
在△ABC中,∵a2+c2=b2
∴ ∠B=90°
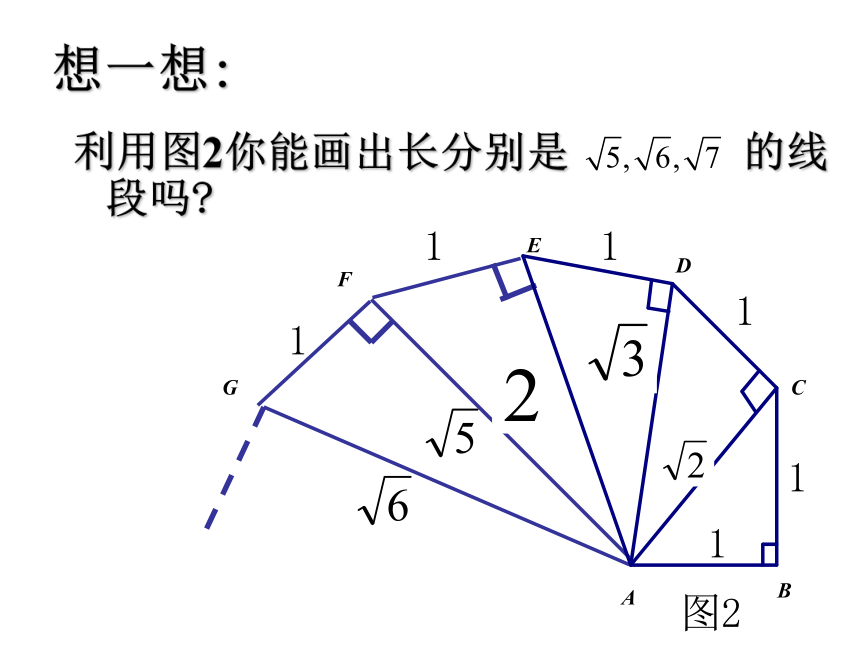
想一想:
利用图2你能画出长分别是 的线段吗?
1
1
1
1
A
B
C
D
E
F
G
周长是:32;
练一练:
3.如图3,求四边形ABCD的周长.
图3
4、如图,等边三角形ABC的边长是6.求△ABC的面积.
D
5.如图,在△ABC中,AB=13,BC=10, BC边上的高AD=12.
求AC.
例2、如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.
求AC.
做一做:
做一做:
6.如图,在△ABC中, AB=13,AD=12,AC=15, CD=9.
求△ABC的面积.
7.一个零件的形状如图所示,已知∠A=∠CBD=90°,AC=3 cm,AB=4 cm,BD=12 cm,求CD的长
解:∵在Rt△ABC中,BC2=AC2+AB2=32+42=25,∴BC=5 在Rt△BDC中,CD2=BC2+BD2 =52+122=169∴CD=13.答:CD的长为13(cm)
8.已知:如图,在Rt△ABC中,两直角边AC=5,BC=12.求斜边上的高CD的长。
探究问题二利用勾股定理求一般三角形的边长
D
10.如图,在一棵树的10m高的B处,有两只猴子,一只猴子爬到树下走到离树20m处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树的高度。
11. 小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为_________米
第2课时 勾股定理的应用
[归纳] 勾股定理揭示了直角三角形____________之间的关系,在应用勾股定理解决实际问题时,一般要先画出示意图,将实际问题转化为_______________问题来解决.
三边
直角三角形
第2课时 勾股定理的应用
探究问题一 勾股定理在实际生活中的应用
12. 如图,一架2.5米长的梯子斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端下滑0.4米,则梯足将向外移__米.
13.如图,有一个“工”字形的机器零件.它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A、B两点之间的距离为__________cm.
A
14.在直线l上依次摆放着七个正方形(如图),已知斜放置的三个正方形的面积分别是a,b,c,正放置的四个正方形的面积依次是S1, S2 ,S3 ,S4 ,则S1+ S2 +S3 +S4 =______ .
15.在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?
16如图所示,在长方形ABCD中,AB=8,BC=4,现将长方形沿AC折叠,点D落在点E处,且CE与AB交于点F,求AF
探究问题二 利用勾股定理寻找最短线路
第2课时 勾股定理的应用
17 如图是一个三级台阶,它的每一级的长、宽和高分别等于100 cm,60 cm和20 cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路的长是多少?
第2课时 勾股定理的应用
[解析]由于蚂蚁沿台阶爬行,故需把台阶展开成平面图形,根据两点之间线段最短和勾股定理可求解.
第2课时 勾股定理的应用
[归纳总结] 最短距离问题是勾股定理在实际中的具体应用,一般求最短距离要将“立体问题”转化为“平面问题”,再利用“两点之间线段最短”或“垂线段最短”以及“勾股定理”等知识来解决.这类问题涉及的几何体主要有长方体、正方体、圆柱体等.在将几何体的表面展开时,要注意确定展开图中两点的相应位置.将几何体表面展开时,可能会有几种情况,有时可能会有几种不同的答案,这时应通过分析、比较得出符合题意的答案.
第2课时 勾股定理的应用
第2课时 勾股定理的应用
1、如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )。
A.7m B.8m C.9m D.10m
8m
2m
8m
·
2、如图,圆柱的高为5㎝,底面周长为24㎝,在圆柱下底面有一只蚂蚁,它从点A出发,沿着圆柱的表面爬行到对面的点B,它爬行的最短路程是 cm.
·
·
A
B
C
3。在一次地震中,一棵20米高的大树被折断了,
地震过后 ,测量了有关数据,测得树梢着地
点到树根的距离为6米.这棵大树折断处离
地面有多高?
B
第2课时 勾股定理的应用
4.如图18-1-20,在一场冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是____米.
2、已知,在△ABC中,∠C=900,
AC=5cm,BC=10cm,将△ABC折叠,使点B
与点A重合,折痕为DE.求CD的长度.
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
z
x
y
图1中的x等于多少?
图1中的y、z等于多少?
1
1
1
1
图1
A
B
C
D
E
a
b
c
A
B
C
b
a
c
图1中的a ,b,c有怎样的关系?
∴a2+b2=c2
在△ABC中,∵∠C=90°
∴ ∠C=90°
在△ABC中,∵a2+b2=c2
在△ABC中,∵∠B=90°
∴a2+c2=b2
在△ABC中,∵a2+c2=b2
∴ ∠B=90°
想一想:
利用图2你能画出长分别是 的线段吗?
1
1
1
1
A
B
C
D
E
F
G
周长是:32;
练一练:
3.如图3,求四边形ABCD的周长.
图3
4、如图,等边三角形ABC的边长是6.求△ABC的面积.
D
5.如图,在△ABC中,AB=13,BC=10, BC边上的高AD=12.
求AC.
例2、如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.
求AC.
做一做:
做一做:
6.如图,在△ABC中, AB=13,AD=12,AC=15, CD=9.
求△ABC的面积.
7.一个零件的形状如图所示,已知∠A=∠CBD=90°,AC=3 cm,AB=4 cm,BD=12 cm,求CD的长
解:∵在Rt△ABC中,BC2=AC2+AB2=32+42=25,∴BC=5 在Rt△BDC中,CD2=BC2+BD2 =52+122=169∴CD=13.答:CD的长为13(cm)
8.已知:如图,在Rt△ABC中,两直角边AC=5,BC=12.求斜边上的高CD的长。
探究问题二利用勾股定理求一般三角形的边长
D
10.如图,在一棵树的10m高的B处,有两只猴子,一只猴子爬到树下走到离树20m处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树的高度。
11. 小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为_________米
第2课时 勾股定理的应用
[归纳] 勾股定理揭示了直角三角形____________之间的关系,在应用勾股定理解决实际问题时,一般要先画出示意图,将实际问题转化为_______________问题来解决.
三边
直角三角形
第2课时 勾股定理的应用
探究问题一 勾股定理在实际生活中的应用
12. 如图,一架2.5米长的梯子斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端下滑0.4米,则梯足将向外移__米.
13.如图,有一个“工”字形的机器零件.它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A、B两点之间的距离为__________cm.
A
14.在直线l上依次摆放着七个正方形(如图),已知斜放置的三个正方形的面积分别是a,b,c,正放置的四个正方形的面积依次是S1, S2 ,S3 ,S4 ,则S1+ S2 +S3 +S4 =______ .
15.在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?
16如图所示,在长方形ABCD中,AB=8,BC=4,现将长方形沿AC折叠,点D落在点E处,且CE与AB交于点F,求AF
探究问题二 利用勾股定理寻找最短线路
第2课时 勾股定理的应用
17 如图是一个三级台阶,它的每一级的长、宽和高分别等于100 cm,60 cm和20 cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路的长是多少?
第2课时 勾股定理的应用
[解析]由于蚂蚁沿台阶爬行,故需把台阶展开成平面图形,根据两点之间线段最短和勾股定理可求解.
第2课时 勾股定理的应用
[归纳总结] 最短距离问题是勾股定理在实际中的具体应用,一般求最短距离要将“立体问题”转化为“平面问题”,再利用“两点之间线段最短”或“垂线段最短”以及“勾股定理”等知识来解决.这类问题涉及的几何体主要有长方体、正方体、圆柱体等.在将几何体的表面展开时,要注意确定展开图中两点的相应位置.将几何体表面展开时,可能会有几种情况,有时可能会有几种不同的答案,这时应通过分析、比较得出符合题意的答案.
第2课时 勾股定理的应用
