北师大版高中数学必修五第二章第1节正弦定理 课件(共21张PPT)
文档属性
| 名称 | 北师大版高中数学必修五第二章第1节正弦定理 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-24 14:21:32 | ||
图片预览






文档简介
(共21张PPT)
正弦定理(第一课时)
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。
新课导入
给你一根2米高的木杆,一把皮尺.你能利用所学知识来测出塔高吗?
2米木杆
皮尺
新课导入
新课导入
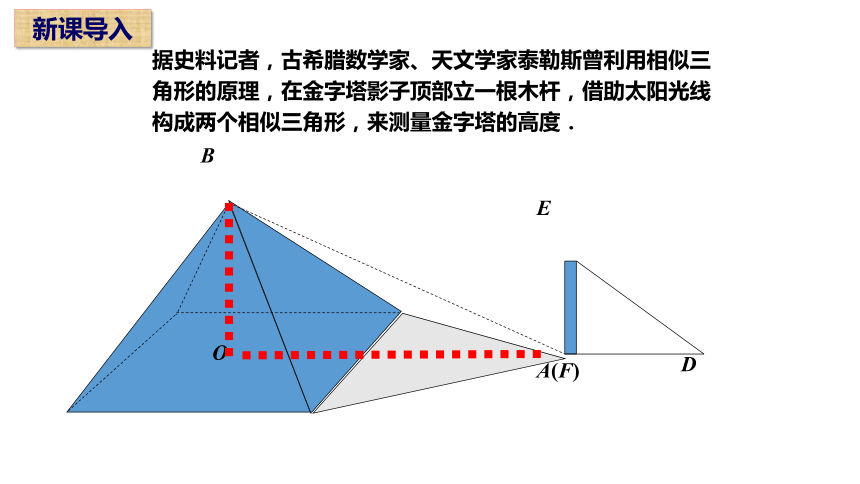
据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
B
E
A(F)
D
O
新课导入
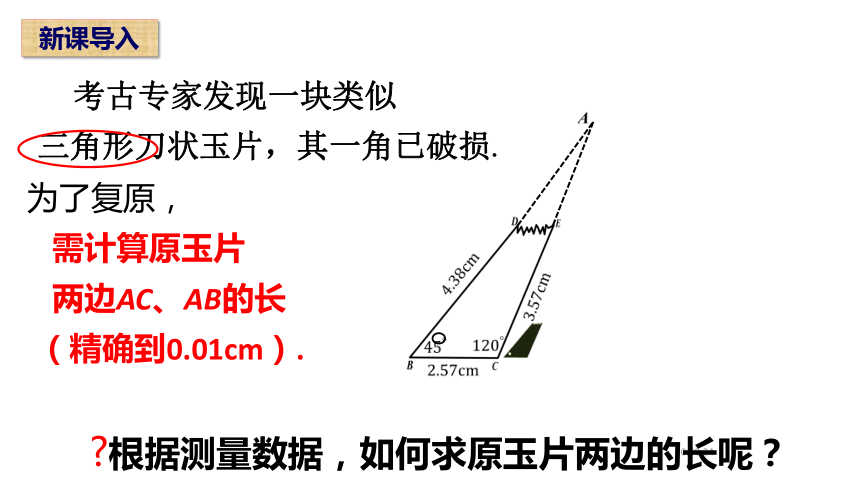
考古专家发现一块类似
三角形刀状玉片,其一角已破损.
为了复原,
11:50:30
新课导入
需计算原玉片
两边AC、AB的长
(精确到0.01cm).
?根据测量数据,如何求原玉片两边的长呢?
在非直角三角形ABC中有这样的关系吗?
A
c
b
a
C
B
探究新知
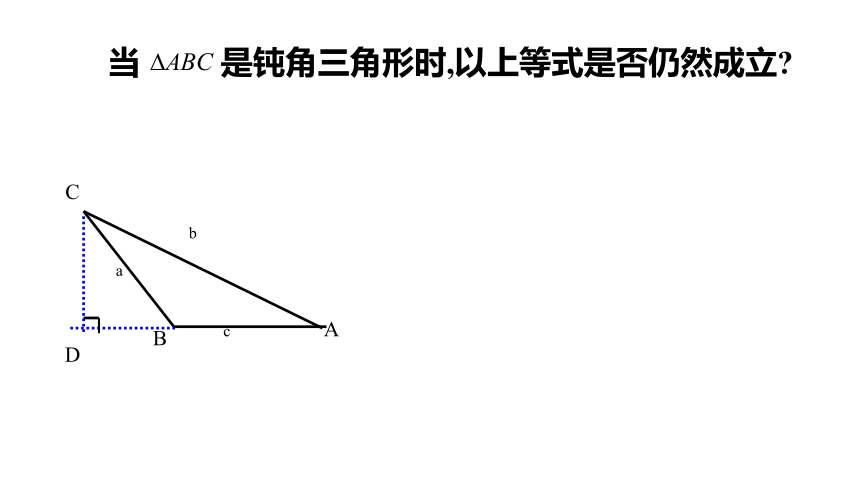
当 是钝角三角形时,以上等式是否仍然成立?
B
A
C
b
c
a
D
正弦定理
2、正弦定理可以解什么类型的三角形问题?
A. 已知两角和任意一边,可以求出其他两边和一角;
B. 已知两边和其中一边的对角,可以求出三角形的其他的边和角。
1、 一般地,把三角形的三个角A,B,C和它的对边a,b,c叫做三角形的
元素已知三角形的几个元素求其他元素的过程叫做解三角形
基础训练一 (两角和一边)
1、 在 中,已知 ,求a。
基础训练一 (两角和一边)
1、 在 中,已知 ,求a。
测量数据:
B,. 为了复原,需计算原玉片两边AC、AB的长
(精确到0.01cm).(参考数据 )
解:在
正弦定理
则
=
=
11:50:30
基础训练2 (两边和其中一边所对的角)
基础训练2 (两边和其中一边所对的角)
(1) 已知两角及任意一边,可以求出其他两边和另一角;
(2)已知两边和其中一边的对角,可以求出三角形的其 他的边和角。(此时可能有一解、二解、无解)
正弦定理
课堂小结
课后探究:
你还可以用其它方法证明正弦定理吗?
11:50:30
探究
11:50:30
探究
11:50:30
探究
A的范围
a,b关系
解的情况
(按角A分类)
A为钝角或直角
A为锐角
a>b
a≤b
a≥b
a <b且a<bsinA
a <b且a=bsinA
a <b且a>bsinA
一解
无解
一解
无解
一解
两解
讨论已知两边和一边对角的斜三角形的解:
探究
正弦定理(第一课时)
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。
新课导入
给你一根2米高的木杆,一把皮尺.你能利用所学知识来测出塔高吗?
2米木杆
皮尺
新课导入
新课导入
据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
B
E
A(F)
D
O
新课导入
考古专家发现一块类似
三角形刀状玉片,其一角已破损.
为了复原,
11:50:30
新课导入
需计算原玉片
两边AC、AB的长
(精确到0.01cm).
?根据测量数据,如何求原玉片两边的长呢?
在非直角三角形ABC中有这样的关系吗?
A
c
b
a
C
B
探究新知
当 是钝角三角形时,以上等式是否仍然成立?
B
A
C
b
c
a
D
正弦定理
2、正弦定理可以解什么类型的三角形问题?
A. 已知两角和任意一边,可以求出其他两边和一角;
B. 已知两边和其中一边的对角,可以求出三角形的其他的边和角。
1、 一般地,把三角形的三个角A,B,C和它的对边a,b,c叫做三角形的
元素已知三角形的几个元素求其他元素的过程叫做解三角形
基础训练一 (两角和一边)
1、 在 中,已知 ,求a。
基础训练一 (两角和一边)
1、 在 中,已知 ,求a。
测量数据:
B,. 为了复原,需计算原玉片两边AC、AB的长
(精确到0.01cm).(参考数据 )
解:在
正弦定理
则
=
=
11:50:30
基础训练2 (两边和其中一边所对的角)
基础训练2 (两边和其中一边所对的角)
(1) 已知两角及任意一边,可以求出其他两边和另一角;
(2)已知两边和其中一边的对角,可以求出三角形的其 他的边和角。(此时可能有一解、二解、无解)
正弦定理
课堂小结
课后探究:
你还可以用其它方法证明正弦定理吗?
11:50:30
探究
11:50:30
探究
11:50:30
探究
A的范围
a,b关系
解的情况
(按角A分类)
A为钝角或直角
A为锐角
a>b
a≤b
a≥b
a <b且a<bsinA
a <b且a=bsinA
a <b且a>bsinA
一解
无解
一解
无解
一解
两解
讨论已知两边和一边对角的斜三角形的解:
探究
