人教版高中物理选修3-2 4.4法拉第电磁感应定律2(15张PPT)
文档属性
| 名称 | 人教版高中物理选修3-2 4.4法拉第电磁感应定律2(15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 283.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-20 16:16:41 | ||
图片预览



文档简介
(共15张PPT)
4.4 法拉第电磁感应定律
第2课时
1.会用E= 和E=BLV求解电动势。
2.会区分平均感应电动势和瞬时感应电动势。
3.理解反电动势的定义。
学习目标
问题导学(阅读P15-16)
1.导体杆垂直切割磁感线运动时,感应电动势表达式?若V与B成ɑ角感应电动势表达式?
2.什么是反电动势?起什么作用?
电动机转动时,线圈中也会产生感应电动势,这个感应电动势总要削弱电源电动势的作用,我们把这个电动势称为反电动势。
作用:阻碍线圈的转动
精讲:一导体作垂直切割磁感线运动
如图所示闭合线圈一部分导体ab处于匀强磁场中,磁感应强度是B,ab以速度v匀速切割磁感线,求产生的感应电动势
回路在时间t内增大的面积为:
ΔS=LvΔt
穿过回路的磁通量的变化为:
产生的感应电动势为:
注意公式使用条件:
B、L、V两两垂直
思考:若ab杆绕a或b转动,如何求感应电动势?
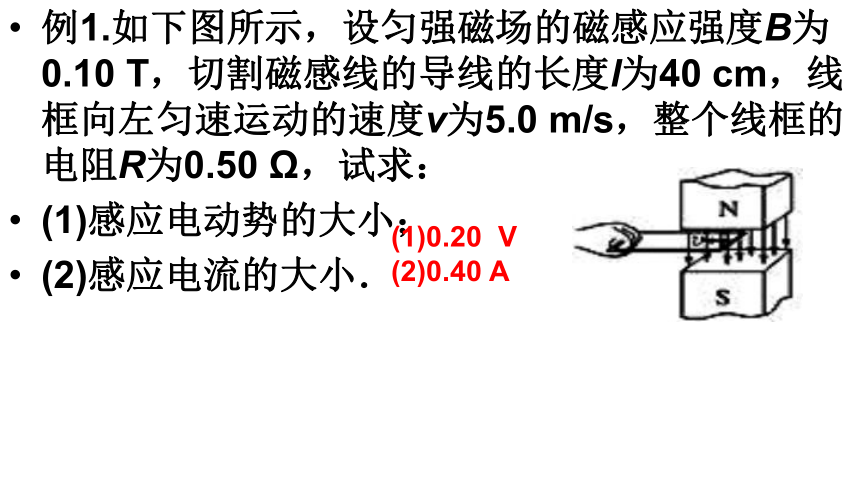
例1.如下图所示,设匀强磁场的磁感应强度B为0.10 T,切割磁感线的导线的长度l为40 cm,线框向左匀速运动的速度v为5.0 m/s,整个线框的电阻R为0.50 Ω,试求:
(1)感应电动势的大小;
(2)感应电流的大小.
(1)0.20 V
(2)0.40 A
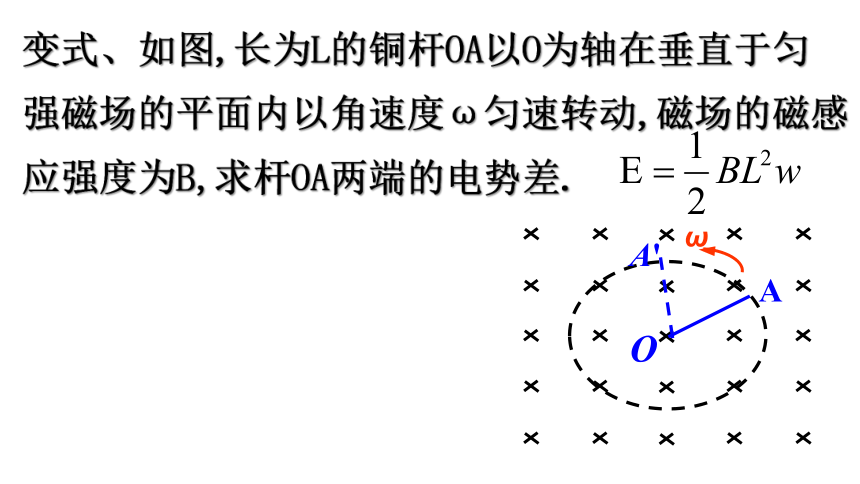
变式、如图,长为L的铜杆OA以O为轴在垂直于匀强磁场的平面内以角速度ω匀速转动,磁场的磁感应强度为B,求杆OA两端的电势差.
V1
V2
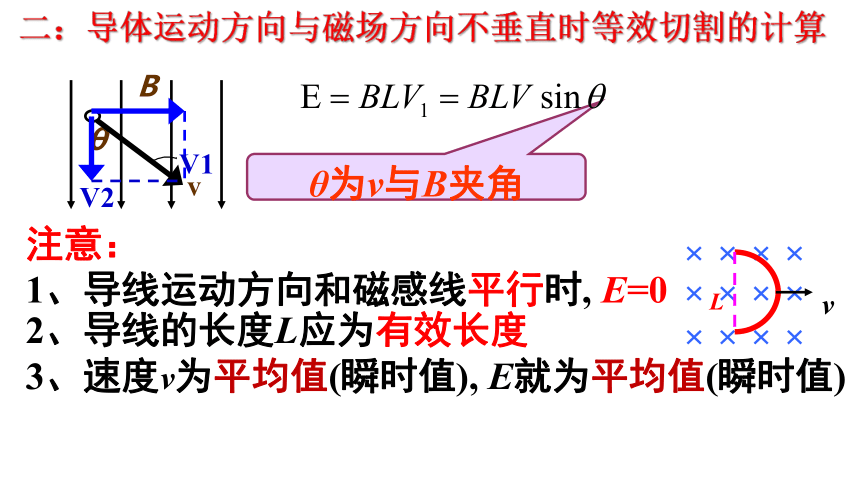
注意:
2、导线的长度L应为有效长度
1、导线运动方向和磁感线平行时, E=0
3、速度v为平均值(瞬时值), E就为平均值(瞬时值)
L
θ为v与B夹角
二:导体运动方向与磁场方向不垂直时等效切割的计算
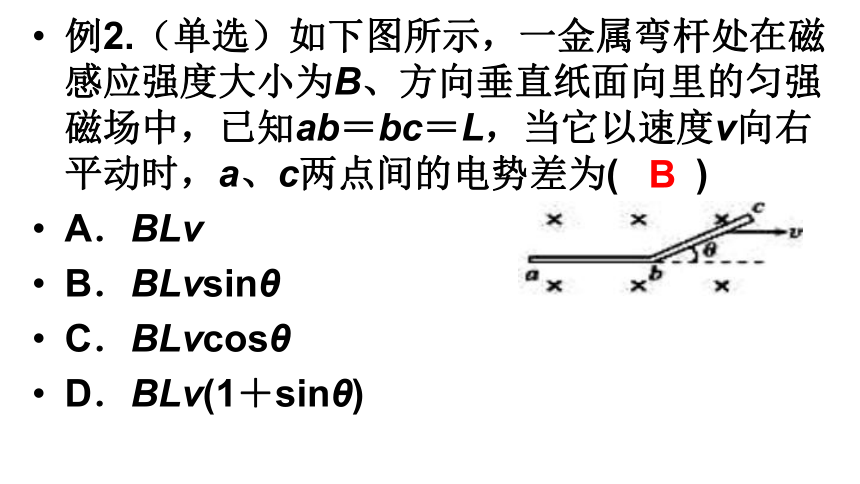
例2.(单选)如下图所示,一金属弯杆处在磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,已知ab=bc=L,当它以速度v向右平动时,a、c两点间的电势差为( )
A.BLv
B.BLvsinθ
C.BLvcosθ
D.BLv(1+sinθ)
B
变式.(多选)如图所示的几种情况,金属导体中产生的感应电动势为Blv的是( )
A. B.
C. D.
BCD
三:
(2)E=BLVsinθ大多用来求瞬时感应电动势, 与某个时刻或某个位置对应.
(1) 求出的是平均感应电动势, 与
某段时间或某个过程对应;
(3)公式②中v若代表平均速度,则E为平均感应电动势。
四:反电动势
反电动势是指有反抗电流发生改变的趋势而产生电动势,其本质上属于感应电动势。反电动势一般出现在电磁线圈中,如继电器线圈、电磁阀、接触器线圈、电动机、电感等。
例3.(单选)关于反电动势,下列说法中正确的是( )
A. 只要线圈在磁场中运动就能产生反电动势
B. 只要穿过线圈的磁通量变化,就能产生反电动势
C. 电动机在转动时线圈内产生反电动势
D. 反电动势就是发电机产生的电动势
C
一、法拉第电磁感应定律
1.内容:
2.公式:
课堂小结
二、导体切割磁感线时的感应电动势
1、导体垂直切割:
2.导体倾斜切割:
1.(单选)如图所示,在竖直向下的匀强磁场中,将一个水平放置的金属棒ab以水平初速度v0抛出,设运动的整个过程中棒的方向不变且不计空气阻力,则金属棒在运动过程中产生的感应电动势大小将( )
A. 越来越大
B. 越来越小
C. 保持不变
D. 无法确定
课堂训练
C
2、如图,有一匀强磁场 B = 1.0×10-3 T,在垂直磁场的平面内,有一金属棒AO,绕平行于磁场的 O 轴顺时针转动,已知棒长 L = 0.20 m,角速度 ω = 20 rad/s,求:
(1)O,A哪端电势更高?
(2)棒产生的感应电动势有多大?
4×10-4V
A端
3.如下图所示,导体棒ab长L,沿倾角为α的斜导轨以速度v下滑,匀强磁场磁感应强度为B,方向竖直向上,求:导体棒ab中产生的感应电动势为多大?
BLvcosα
4.如图,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻不计,在M 和P 之间接有R=3.0Ω的定值电阻,导体棒长ab=0.5m,其电阻为r=1.0Ω,与导轨接触良好.整个装置处于方向竖直向下的匀强磁场中B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.
(1)ab中的电流多大? ab两点间的电压多大?
(2)维持ab做匀速运动的外力多大?
(3)ab向右运动1m的过程中,外力做的功是多少?
电路中产生的热量是多少?
WF=0.1J; Q=0.1J
I=0.5A;
U=1.5V
F=0.1N
W安=Q
4.4 法拉第电磁感应定律
第2课时
1.会用E= 和E=BLV求解电动势。
2.会区分平均感应电动势和瞬时感应电动势。
3.理解反电动势的定义。
学习目标
问题导学(阅读P15-16)
1.导体杆垂直切割磁感线运动时,感应电动势表达式?若V与B成ɑ角感应电动势表达式?
2.什么是反电动势?起什么作用?
电动机转动时,线圈中也会产生感应电动势,这个感应电动势总要削弱电源电动势的作用,我们把这个电动势称为反电动势。
作用:阻碍线圈的转动
精讲:一导体作垂直切割磁感线运动
如图所示闭合线圈一部分导体ab处于匀强磁场中,磁感应强度是B,ab以速度v匀速切割磁感线,求产生的感应电动势
回路在时间t内增大的面积为:
ΔS=LvΔt
穿过回路的磁通量的变化为:
产生的感应电动势为:
注意公式使用条件:
B、L、V两两垂直
思考:若ab杆绕a或b转动,如何求感应电动势?
例1.如下图所示,设匀强磁场的磁感应强度B为0.10 T,切割磁感线的导线的长度l为40 cm,线框向左匀速运动的速度v为5.0 m/s,整个线框的电阻R为0.50 Ω,试求:
(1)感应电动势的大小;
(2)感应电流的大小.
(1)0.20 V
(2)0.40 A
变式、如图,长为L的铜杆OA以O为轴在垂直于匀强磁场的平面内以角速度ω匀速转动,磁场的磁感应强度为B,求杆OA两端的电势差.
V1
V2
注意:
2、导线的长度L应为有效长度
1、导线运动方向和磁感线平行时, E=0
3、速度v为平均值(瞬时值), E就为平均值(瞬时值)
L
θ为v与B夹角
二:导体运动方向与磁场方向不垂直时等效切割的计算
例2.(单选)如下图所示,一金属弯杆处在磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,已知ab=bc=L,当它以速度v向右平动时,a、c两点间的电势差为( )
A.BLv
B.BLvsinθ
C.BLvcosθ
D.BLv(1+sinθ)
B
变式.(多选)如图所示的几种情况,金属导体中产生的感应电动势为Blv的是( )
A. B.
C. D.
BCD
三:
(2)E=BLVsinθ大多用来求瞬时感应电动势, 与某个时刻或某个位置对应.
(1) 求出的是平均感应电动势, 与
某段时间或某个过程对应;
(3)公式②中v若代表平均速度,则E为平均感应电动势。
四:反电动势
反电动势是指有反抗电流发生改变的趋势而产生电动势,其本质上属于感应电动势。反电动势一般出现在电磁线圈中,如继电器线圈、电磁阀、接触器线圈、电动机、电感等。
例3.(单选)关于反电动势,下列说法中正确的是( )
A. 只要线圈在磁场中运动就能产生反电动势
B. 只要穿过线圈的磁通量变化,就能产生反电动势
C. 电动机在转动时线圈内产生反电动势
D. 反电动势就是发电机产生的电动势
C
一、法拉第电磁感应定律
1.内容:
2.公式:
课堂小结
二、导体切割磁感线时的感应电动势
1、导体垂直切割:
2.导体倾斜切割:
1.(单选)如图所示,在竖直向下的匀强磁场中,将一个水平放置的金属棒ab以水平初速度v0抛出,设运动的整个过程中棒的方向不变且不计空气阻力,则金属棒在运动过程中产生的感应电动势大小将( )
A. 越来越大
B. 越来越小
C. 保持不变
D. 无法确定
课堂训练
C
2、如图,有一匀强磁场 B = 1.0×10-3 T,在垂直磁场的平面内,有一金属棒AO,绕平行于磁场的 O 轴顺时针转动,已知棒长 L = 0.20 m,角速度 ω = 20 rad/s,求:
(1)O,A哪端电势更高?
(2)棒产生的感应电动势有多大?
4×10-4V
A端
3.如下图所示,导体棒ab长L,沿倾角为α的斜导轨以速度v下滑,匀强磁场磁感应强度为B,方向竖直向上,求:导体棒ab中产生的感应电动势为多大?
BLvcosα
4.如图,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻不计,在M 和P 之间接有R=3.0Ω的定值电阻,导体棒长ab=0.5m,其电阻为r=1.0Ω,与导轨接触良好.整个装置处于方向竖直向下的匀强磁场中B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.
(1)ab中的电流多大? ab两点间的电压多大?
(2)维持ab做匀速运动的外力多大?
(3)ab向右运动1m的过程中,外力做的功是多少?
电路中产生的热量是多少?
WF=0.1J; Q=0.1J
I=0.5A;
U=1.5V
F=0.1N
W安=Q
