2020年春人教版数学七年级下册同步练习课件:5.1.2垂线(共22张PPT)
文档属性
| 名称 | 2020年春人教版数学七年级下册同步练习课件:5.1.2垂线(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览






文档简介
课件22张PPT。 垂 线?第五章5.1.2 垂 线核心目标……………..…课堂导案……………..…1 课前学案……………..…23课后练案……………..…4拓展提升……………..…5核心目标理解垂线、垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线;掌握垂线的性质及点到直线的距离的概念.
课前学案1.直线AB、CD相交于点O,∠AOD=90°,直线AB与
CD的关系是___________,记作________, 其中
的一条直线叫做另一条直线的________,交 点O
叫做________.垂足互相垂直2.过一点有且只有__________直线与已知直线垂直.3.如图,如果AB⊥CD,那么有
∠AOC=_______;如果∠AOD
=90°, 那么有________.垂线90°AB⊥CDAB⊥CD一条课前学案4.连接直线外一点与直线上各点的所有线段中,
____________最短,简单说成____________.5.直线外一点到这条直线的__________的长度,
叫做点到直线的距离.垂线段垂线段垂线段最短课堂导案【例1】 如图,三条直线相交于点O.若CO⊥AB,
∠1=52°,则∠2等于( )
A.37° B.28°
C.38° D.47°
【解析】首先根据垂直定义可得∠BOC=90°,再由
∠1=52°可得∠BOE的度数,再利用对顶
【点拔】此题主要考查了垂直的概念,得出∠BOE
的度数是解题的关键.
知识点1:垂线的概念和性质C课堂导案
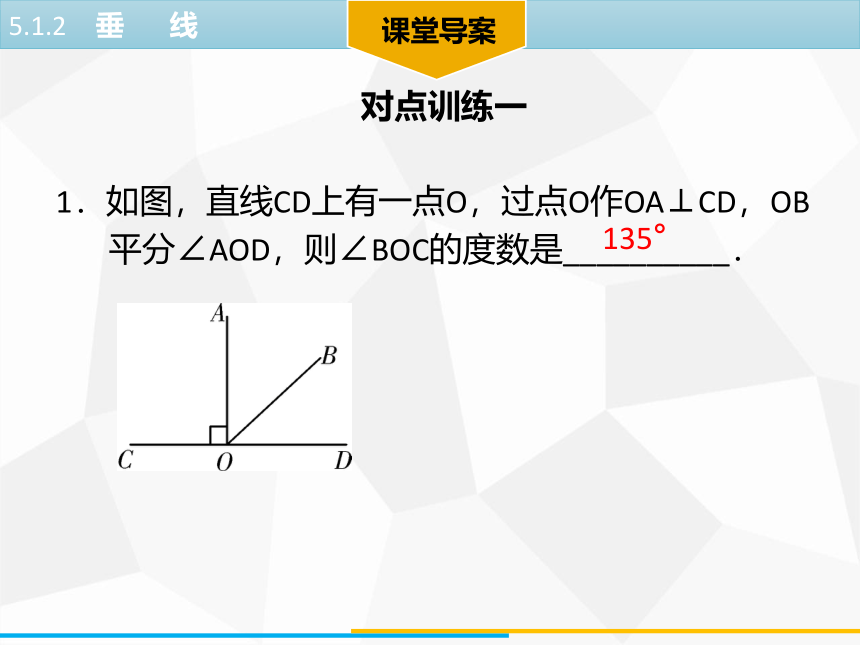
1.如图,直线CD上有一点O,过点O作OA⊥CD,OB
平分∠AOD,则∠BOC的度数是__________.对点训练一135°课堂导案
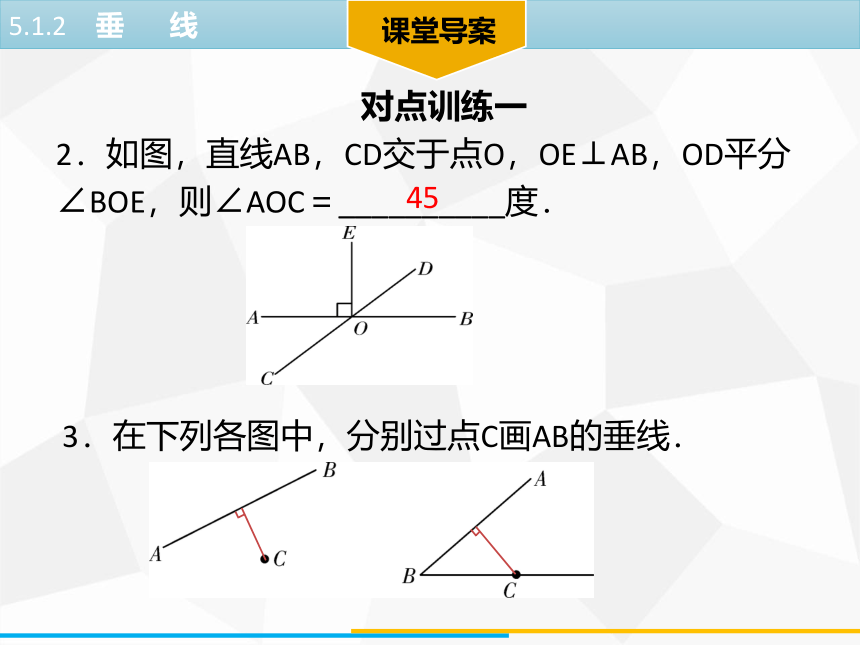
2.如图,直线AB,CD交于点O,OE⊥AB,OD平分∠BOE,则∠AOC=__________度.对点训练一453.在下列各图中,分别过点C画AB的垂线.课堂导案【例2】 如图,要把河中的水引到水池A中,应在河岸
B处(AB⊥CD)开始挖渠才能使水渠的长度最短
,这样做依据的几何学原理是 ( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
知识点2:垂线段的性质和点到直线的距离D课堂导案【解析】 连接直线外一点与直线上所有点的连线,垂
线段最短,所以,沿AB开渠,能使所开的渠
道最短.
【点拔】 本题是垂线段最短在实际生活中的应用,体
现了数学的实际运用价值.
课堂导案对点训练二4.如图,在铁路旁有一李庄,现要建一火车站,为了
使李庄人乘车最方便,请你在铁路线上选一点来建
火车站,应建在 ( )
A.A点 B.B点 C.C点 D.D点A课堂导案对点训练二5.如图是小亮跳远时沙坑的示意图,测量成绩时先使
皮尺从后脚跟的点A处开始并与起跳线l于点B处成
直角,然后记AB的长度,这样做的理由是 ( )
A.垂线段最短
B.过两点有且只有一条直线
C.两点之间线段最短
D.过一点可以做无数条直线A课堂导案对点训练二6.如图,点B到直线AC的距离是线段( )的长度.
A.AB B.CB
C.BD D.ACB课后练案7.如图,直线AB、CD、EF相交于O,CD⊥EF,∠AOC=30°,则∠AOF=__________,∠BOC=__________.8.如图,直线AB、CD交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD=_______度.
60°125°150°课后巩固9.如图,AB,CD相交于点O,OE⊥AB,垂足为O,
∠COE=44°,则∠AOD=__________.10.如图,AB⊥l,垂足为B,C为l上异于B的点,
则AB<AC的理由是____________________.134°垂线段最短课后练案11.完成两个推理:
(1)∵AB⊥CD(已知),
∴∠ACD=________,(________________)
(2)∵∠ACD=90°(已知),
∴_________________(________________)90°垂直的定义AB⊥CD垂直的定义课后练案12.如图,AC⊥a,AB⊥b,垂足分别为A、B,则A点到直线b的距离是线段________的长.AB第12题图
课后练案13.已知,如图,OA⊥OB,直线CD过O点,且∠AOC=30°,求∠BOD的度数.
∵OA⊥OB,
∴∠AOB=90°,又∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=60°,
∴∠BOD=180°-∠BOC=120°.第13题图
课后练案14.如图,直线AB与CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=65°.求:
(1)∠AOC的度数;
(2)∠BOE的度数.(1)∵OF⊥AB,∴∠BOF=90°,又∠DOF=65°,∴∠BOD=∠BOF-∠DOF=25°,∴∠AOC=∠BOD=25°.第14题图
(2)∵OE⊥CD,∴∠DOE=90°,又由(1)得∠BOD=25°,∴∠BOE=∠DOE-∠BOD=65°.拓展提升15.如图所示,直线AB,CD相交于点O,作 ∠DOE=
∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系;
(2)若∠AOC ∶∠AOD=1∶5,求∠EOF的度数.
拓展提升(1)∵OF平分∠AOE,∴∠EOF=?∠AOE.
∵∠EOD=∠BOD,∴∠EOD= ? ∠EOB.
∴∠FOD=∠FOE+∠EOD= ? ∠AOE+ ? ∠EOB
= ?(∠AOE+∠EOB)= ? ∠AOB=90°,
∴OF⊥OD;(2)设∠AOC=x°,∠AOD=5x°,则x°+5x°=180°,
得x°=30°,∴∠AOC=30°.
∴∠EOD=∠BOD=∠AOC=30°.
∴∠AOE=180°-∠AOC-∠EOD=120°,
∴∠EOF= ? ∠AOE=60°.感谢聆听
课前学案1.直线AB、CD相交于点O,∠AOD=90°,直线AB与
CD的关系是___________,记作________, 其中
的一条直线叫做另一条直线的________,交 点O
叫做________.垂足互相垂直2.过一点有且只有__________直线与已知直线垂直.3.如图,如果AB⊥CD,那么有
∠AOC=_______;如果∠AOD
=90°, 那么有________.垂线90°AB⊥CDAB⊥CD一条课前学案4.连接直线外一点与直线上各点的所有线段中,
____________最短,简单说成____________.5.直线外一点到这条直线的__________的长度,
叫做点到直线的距离.垂线段垂线段垂线段最短课堂导案【例1】 如图,三条直线相交于点O.若CO⊥AB,
∠1=52°,则∠2等于( )
A.37° B.28°
C.38° D.47°
【解析】首先根据垂直定义可得∠BOC=90°,再由
∠1=52°可得∠BOE的度数,再利用对顶
【点拔】此题主要考查了垂直的概念,得出∠BOE
的度数是解题的关键.
知识点1:垂线的概念和性质C课堂导案
1.如图,直线CD上有一点O,过点O作OA⊥CD,OB
平分∠AOD,则∠BOC的度数是__________.对点训练一135°课堂导案
2.如图,直线AB,CD交于点O,OE⊥AB,OD平分∠BOE,则∠AOC=__________度.对点训练一453.在下列各图中,分别过点C画AB的垂线.课堂导案【例2】 如图,要把河中的水引到水池A中,应在河岸
B处(AB⊥CD)开始挖渠才能使水渠的长度最短
,这样做依据的几何学原理是 ( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
知识点2:垂线段的性质和点到直线的距离D课堂导案【解析】 连接直线外一点与直线上所有点的连线,垂
线段最短,所以,沿AB开渠,能使所开的渠
道最短.
【点拔】 本题是垂线段最短在实际生活中的应用,体
现了数学的实际运用价值.
课堂导案对点训练二4.如图,在铁路旁有一李庄,现要建一火车站,为了
使李庄人乘车最方便,请你在铁路线上选一点来建
火车站,应建在 ( )
A.A点 B.B点 C.C点 D.D点A课堂导案对点训练二5.如图是小亮跳远时沙坑的示意图,测量成绩时先使
皮尺从后脚跟的点A处开始并与起跳线l于点B处成
直角,然后记AB的长度,这样做的理由是 ( )
A.垂线段最短
B.过两点有且只有一条直线
C.两点之间线段最短
D.过一点可以做无数条直线A课堂导案对点训练二6.如图,点B到直线AC的距离是线段( )的长度.
A.AB B.CB
C.BD D.ACB课后练案7.如图,直线AB、CD、EF相交于O,CD⊥EF,∠AOC=30°,则∠AOF=__________,∠BOC=__________.8.如图,直线AB、CD交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD=_______度.
60°125°150°课后巩固9.如图,AB,CD相交于点O,OE⊥AB,垂足为O,
∠COE=44°,则∠AOD=__________.10.如图,AB⊥l,垂足为B,C为l上异于B的点,
则AB<AC的理由是____________________.134°垂线段最短课后练案11.完成两个推理:
(1)∵AB⊥CD(已知),
∴∠ACD=________,(________________)
(2)∵∠ACD=90°(已知),
∴_________________(________________)90°垂直的定义AB⊥CD垂直的定义课后练案12.如图,AC⊥a,AB⊥b,垂足分别为A、B,则A点到直线b的距离是线段________的长.AB第12题图
课后练案13.已知,如图,OA⊥OB,直线CD过O点,且∠AOC=30°,求∠BOD的度数.
∵OA⊥OB,
∴∠AOB=90°,又∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=60°,
∴∠BOD=180°-∠BOC=120°.第13题图
课后练案14.如图,直线AB与CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=65°.求:
(1)∠AOC的度数;
(2)∠BOE的度数.(1)∵OF⊥AB,∴∠BOF=90°,又∠DOF=65°,∴∠BOD=∠BOF-∠DOF=25°,∴∠AOC=∠BOD=25°.第14题图
(2)∵OE⊥CD,∴∠DOE=90°,又由(1)得∠BOD=25°,∴∠BOE=∠DOE-∠BOD=65°.拓展提升15.如图所示,直线AB,CD相交于点O,作 ∠DOE=
∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系;
(2)若∠AOC ∶∠AOD=1∶5,求∠EOF的度数.
拓展提升(1)∵OF平分∠AOE,∴∠EOF=?∠AOE.
∵∠EOD=∠BOD,∴∠EOD= ? ∠EOB.
∴∠FOD=∠FOE+∠EOD= ? ∠AOE+ ? ∠EOB
= ?(∠AOE+∠EOB)= ? ∠AOB=90°,
∴OF⊥OD;(2)设∠AOC=x°,∠AOD=5x°,则x°+5x°=180°,
得x°=30°,∴∠AOC=30°.
∴∠EOD=∠BOD=∠AOC=30°.
∴∠AOE=180°-∠AOC-∠EOD=120°,
∴∠EOF= ? ∠AOE=60°.感谢聆听
