北师大版数学七年级下册第5章《生活中的轴对称》达标测试卷 含答案解析
文档属性
| 名称 | 北师大版数学七年级下册第5章《生活中的轴对称》达标测试卷 含答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-20 20:51:38 | ||
图片预览




文档简介
北师大版七年级下册第5章《生活中的轴对称》达标测试卷
满分120分
班级:________姓名:________座位:________成绩:________
一.选择题(共10小题,满分30分)
1.下列防疫的图标中是轴对称图形的是( )
A. B.
C. D.
2.如图是一个经过改造的规则为4×7的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是( )
A.1号袋 B.2号袋 C..3号袋 D.4号袋
3.如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B度数为( )
A.30° B.60° C.90° D.120°
4.如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( )
A.5个 B.6个 C.7个 D.8个
5.某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水.某同学用直线(虛线)l表示小河,P,Q两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( )
A. B.
C. D.
6.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为( )
A.12 B.13 C.19 D.20
7.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=26°,则∠A的度数为( )
A.40° B.34° C.36° D.38°
8.如图,△ABC中,BO平分∠ABC,CO平分∠ACB,M,N经过点O,且MN∥BC,若AB=5,△AMN的周长等于12,则AC的长为( )
A.7 B.6 C.5 D.4
9.如图,在△ABC中,AB=AC,分别以点A、点B为圆心,以大于AB长为半径画弧,两弧交点的连线交AC于点D,交AB于点E,连接BD,若∠A=40°,则∠DBC=( )
A.40° B.30° C.20° D.10°
10.如图,△ABC是等边三角形,P是三角形内任意一点,D、E、F分别是AC、AB、BC边上的三点,且PF∥AB,PD∥BC,PE∥AC.若PF+PD+PE=a,则△ABC的边长为( )
A.a B.a C.a D.a
二.填空题(共8小题,满分24分)
11.在线段、直角、等腰三角形、直角三角形中,成轴对称图形的是 .
12.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是 .
13.如图,在△ABC中,AB=AC,BC=10,AD是∠BAC平分线,则BD= .
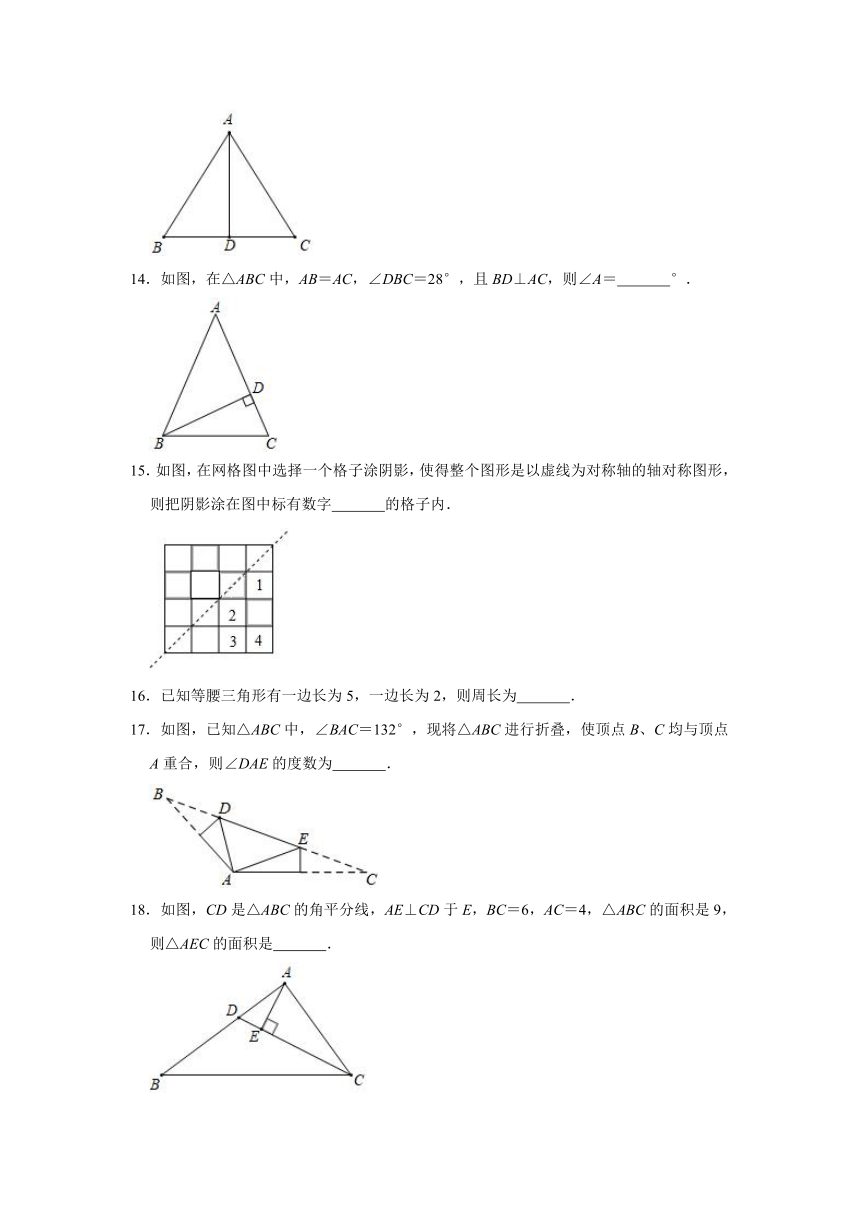
14.如图,在△ABC中,AB=AC,∠DBC=28°,且BD⊥AC,则∠A= °.
15.如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字 的格子内.
16.已知等腰三角形有一边长为5,一边长为2,则周长为 .
17.如图,已知△ABC中,∠BAC=132°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,则∠DAE的度数为 .
18.如图,CD是△ABC的角平分线,AE⊥CD于E,BC=6,AC=4,△ABC的面积是9,则△AEC的面积是 .
三.解答题(共7小题,满分66分)
19.如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.
20.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q;
21.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
22.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,BE⊥BD,DE∥BC,BE与DE交于点E,DE交AB于点F.
(1)若∠A=56°,求∠E的度数;
(2)求证:BF=EF.
23.在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,则BE=CE吗?说明理由;
(2)若∠BAC=45°,BE的延长线与AC垂直相交于点F时,如图2,BD=AE吗?说明理由.
24.在等边△ABC中,
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.
25.如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
(1)若∠B=60°,求∠C的值;
(2)求证:AD是∠EAC的平分线.
参考答案
一.选择题(共10小题)
1.【解答】解:A、不是轴对称图形,不合题意;
B、不是轴对称图形,不合题意;
C、是轴对称图形,符合题意;
D、不是轴对称图形,不合题意.
故选:C.
2.【解答】解:根据轴对称的性质可知,台球走过的路径为:
所以球最后将落入的球袋是4号袋,
故选:D.
3.【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=60°,
∵∠A=30°,
∴∠B=180°﹣∠A﹣∠C=90°,
故选:C.
4.【解答】解:如图所示:
与△ABC成轴对称,顶点在格点上,且位置不同的三角形有8个,
故选:D.
5.【解答】解:作点P关于直线l的对称点C,连接QC交直线l于M.
根据两点之间,线段最短,可知选项C铺设的管道最短.
故选:C.
6.【解答】解:由折叠可知,AD=CD,
∵AB=7,BC=6,
∴△BCD的周长=BC+BD+CD=BC+BD+AD=BC+AB=7+6=13.
故选:B.
7.【解答】解:∵DE⊥AB,DC⊥BC,DE=DC,
∴BD平分∠ABC,
∴∠EBD=∠CBD=26°,
∴∠A=90°﹣∠ABC=90°﹣2×26°=38°.
故选:D.
8.【解答】解:∵BO平分∠CBA,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵AB=5,△AMN的周长等于12,
∴△AMN的周长=AM+MN+AN=AB+AC=5+AC=12,
∴AC=7,
故选:A.
9.【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°﹣40°)=70°,
∵AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=30°,
故选:B.
10.【解答】解:延长EP交BC于点G,延长FP交AC于点H,如图所示:
∵PF∥AB,PD∥BC,PE∥AC,
∴四边形AEPH、四边形PDCG均为平行四边形,
∴PE=AH,PG=CD.
又∵△ABC为等边三角形,
∴△FGP和△HPD也是等边三角形,
∴PF=PG=CD,PD=DH,
∴PE+PD+PF=AH+DH+CD=AC,
∴AC=a;
故选:D.
二.填空题(共8小题)
11.【解答】解:线段的垂直平分线所在的直线是对称轴,是轴对称图形,符合题意;
直角的角平分线所在的直线就是对称轴,是轴对称图形,符合题意;
等腰三角形底边中线所在的直线是对称轴,是轴对称图形,符合题意;
直角三角形不一定是轴对称图形,不符合题意.
故成轴对称图形的是:线段、直角、等腰三角形.
故答案为:线段、直角、等腰三角形.
12.【解答】解:过P作PE⊥OA于点E,
∵点P是∠AOB平分线OC上一点,PD⊥OB,
∴PE=PD,
∵PD=2,
∴PE=2,
∴点P到边OA的距离是2.
故答案为2.
13.【解答】解:∵AB=AC,∠BAC的平分线交BC边于点D,BC=10,
∴BD=CD=BC=5,
故答案为:5.
14.【解答】解:∵BD是AC边上的高,
∴∠DBC+∠C=90°,∠DBC=28°.
∴∠C=62°
∵AB=AC,
∴∠A=180°﹣2∠C=180°﹣124°=56°,
故答案为:56.
15.【解答】解:如图所示,
把阴影凃在图中标有数字3的格子内所组成的图形是轴对称图形,
故答案为:3.
16.【解答】解:①若5为腰长,2为底边长,
∵5,5,2能组成三角形,
∴此时周长为:5+5+2=12;
②若2为腰长,5为底边长,
∵2+2=4<5,
∴不能组成三角形,故舍去;
∴周长为12.
故答案为:12.
17.【解答】解:如图,∵∠BAC=132°,
∴∠B+∠C=180°﹣132°=48°;
由题意得:∠B=∠DAB(设为α),∠C=∠EAC(设为β),
∴∠ADE=2α,∠AED=2β,
∴∠DAE=180°﹣2(α+β)=180°﹣96°=84°,
故答案为:84°.
18.【解答】解:延长AE交BC于F,
∵CD是△ABC的角平分线,
∴∠ACE=∠FCE,
∵AE⊥CD于E,
∴∠AEC=∠CEF=90°,
∵CE=CE,
∴△ACE≌△FCE(ASA),
∴CF=AC=4,
∵BC=6,
∴BF=2,
∵△ABC的面积是9,
∴S△ACF=9×=6,
∴△AEC的面积=S△ACF=3,
故答案为:3.
三.解答题(共7小题)
19.【解答】解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°,
∴∠C=30°,
∴∠ABC=2∠C=60°.
20.【解答】解:(1)如图,点M即为所求.
(2)如图,点E,点F即为所求.
21.【解答】解:(1)∵DM是线段AB的垂直平分线,
∴DA=DB,
同理,EA=EC,
∵△ADE的周长5,
∴AD+DE+EA=5,
∴BC=DB+DE+EC=AD+DE+EA=5(cm);
(2)∵△OBC的周长为13,
∴OB+OC+BC=13,
∵BC=5,
∴OB+OC=8,
∵OM垂直平分AB,
∴OA=OB,
同理,OA=OC,
∴OA=OB=OC=4(cm).
22.【解答】解:(1)∵AB=AC,∠A=56°,
∴∠ABC=(180°﹣56°)=62°,
∵BD平分∠ABC,
∴∠DBF=∠DBC=,
∵DE∥BC,
∴∠EDB=∠DBC=31°,
∵BE⊥BD,
∴∠DBE=90°,
∴∠E=90°﹣31°=59°;
(2)∵∠EDB=∠DBF=31°,
∴∠E=∠EBF=59°,
∴BF=EF.
23.【解答】解:(1)成立.
理由:∵AB=AC,D是BC的中点,
∴∠BAE=∠CAE.
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)成立.
理由:∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF,
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,,
∴△AEF≌△BCF(ASA),
∴AE=BC,
∵BD=BC,
∴BD=AE.
24.【解答】解:(1)∵△ABC为等边三角形
∴∠B=60°
∴∠APC=∠BAP+∠B=80°
∵AP=AQ
∴∠AQB=∠APC=80°,
①补全图形如图所示,
②证明:过点A作AH⊥BC于点H,如图.
由△ABC为等边三角形,AP=AQ,
可得∠PAB=∠QAC,
∵点Q,M关于直线AC对称,
∴∠QAC=∠MAC,AQ=AM
∴∠MAC+∠PAC=∠PAB+∠PAC=60°,
∴△APM为等边三角形
∴PA=PM.
25.【解答】(1)解:∵∠B=60°,∠BDA=∠BAD,
∴∠BAD=∠BDA=60°,
∴AB=AD,
∵CD=AB,
∴CD=AD,
∴∠DAC=∠C,
∴∠BDA=∠DAC+∠C=2∠C,
∵∠BAD=60°,
∴∠C=30°;
(2)证明:延长AE到M,使EM=AE,连接DM,
在△ABE和△MDE中,
,
∴△ABE≌△MDE,
∴∠B=∠MDE,AB=DM,
∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM,
在△MAD与△CAD,,
∴△MAD≌△CAD,
∴∠MAD=∠CAD,
∴AD是∠EAC的平分线.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
