2020春华师版九下数学26.1二次函数课件(33张ppt)
文档属性
| 名称 | 2020春华师版九下数学26.1二次函数课件(33张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 626.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览








文档简介
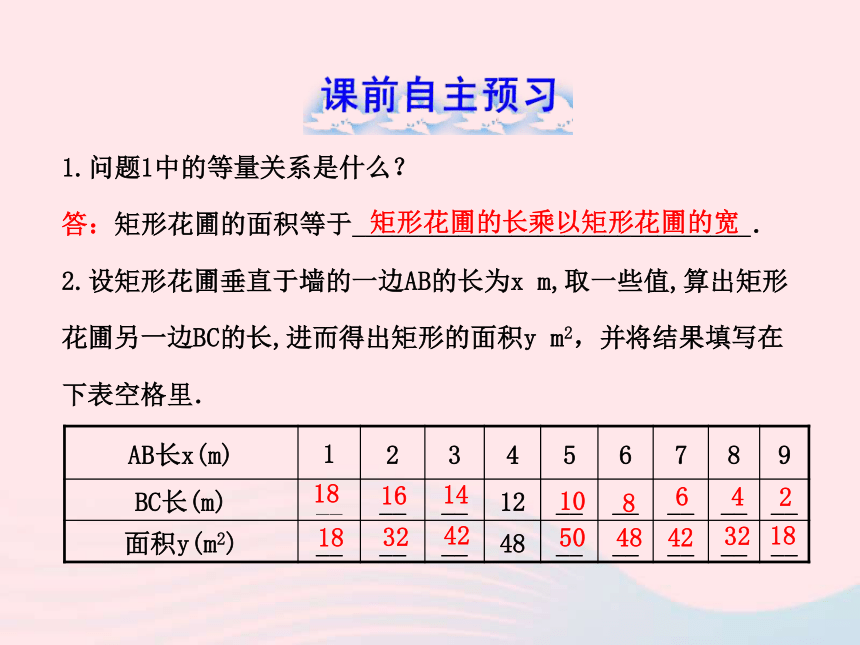
课件33张PPT。§26.1 二次函数 1.问题1中的等量关系是什么?
答:矩形花圃的面积等于______________________________.
2.设矩形花圃垂直于墙的一边AB的长为x m,取一些值,算出矩形
花圃另一边BC的长,进而得出矩形的面积y m2,并将结果填写在
下表空格里.181614108642矩形花圃的长乘以矩形花圃的宽1832425048423218通过填写表格可以发现当x的值为__时,y的值最大,为___.
即在问题1中垂直于墙的一边AB的长为__ m,另一边BC的长为
__ m时,得到的矩形花圃的面积最大.5505103.在问题1中AB(x)是否可以任意取值?x的取值范围是什么?
答:____________________________________.
4.在问题1中,当AB的长(x)确定后,矩形的面积(y)也随之确定,y
是x的_____,它们之间的函数关系式为
y=_________或y=_________.x不能任意取值.x的取值范围是0<x<10x(20-2x)-2x2+20x函数5.在问题2中等量关系是什么?
答:_________________________.
6.问题2中,设每件商品降价x元,该商品每天的利润为y元,则y是
x的______.函数关系式为:y=___________________或者为y=
________________.其中x表示每件商品降价的钱数,最小降价为
__元,最大降价为__元,因此x的取值范围为________.利润=(售价-进价)×销售量(10-x-8)(100+100x)-100x2+100x+200020≤x≤2函数7.二次函数的定义:形如y=_________(a,b,c是常数,a___0)
的函数叫做二次函数,其中x是_______,__是二次项系数,__
是一次项系数,__是常数项.
【点拨】注意二次函数的二次项的系数不为0是二次函数概念的一
部分.ax2+bx+c≠自变量abc【预习思考】1.二次函数要满足的三个条件是什么?
提示:(1)自变量x的最高次数是2;
(2)a≠0;
(3)右边是关于自变量x的整式,自变量x不能出现在分母中或根号
里.2.函数y=(x-3)(x+2)-x2是二次函数吗?
提示:不是.因为函数y=(x-3)(x+2)-x2整理后化为y=-x-6,它是
一次函数,不是二次函数. 二次函数的定义
【例1】已知函数y=(m2+m)xm2-2m+2.
(1)当函数是二次函数时,求m的值;
(2)当函数是一次函数时,求m的值.
【解题探究】
1.在函数y=(m2+m)xm2-2m+2中,自变量x的系数是m2+m,次数是
m2-2m+2. 2.若y=(m2+m)xm2-2m+2为二次函数,则自变量x的系数和次数应分别
等于什么?m的值等于什么?
答:x的系数不为0,即m2+m≠0,解得m≠0且m≠-1;x的次数为2,
即m2-2m+2=2,解得m=0或m=2,所以m=2.3.若y=(m2+m)xm2-2m+2为一次函数,则自变量x的系数和次数应分
别等于什么?m的值又等于什么?
答:x的系数不为0,即m2+m≠0,解得m≠0且m≠-1;x的次数为1,
即m2-2m+2=1,解得m1=m2=1.所以m=1. _______________________________【互动探究】
二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有
什么联系?
提示:如果把变量y换成一个常数,那么二次函数就是一个一元
二次方程了.【规律总结】
判断二次函数的三步法【跟踪训练】
1.下列函数中,是二次函数的是( )
(A)y=8x2+1 (B)y=8x+1
(C)y= (D)y= +1
【解析】选A.A:符合二次函数的y=ax2+bx+c(a≠0)的形式,是
二次函数,正确;B:是一次函数,错误;C:是反比例函数,错误;
D:自变量x在分母中,不是二次函数,错误.2.若函数y=(m-4)x3m2-2m-3是二次函数,求m的值.
【解析】根据题意得
解得
∴m=-1或m= 实际问题中的二次函数关系
【例2】(9分)在一块长方形镜面玻璃的四周镶上与它的周长相
等的边框,制成一面镜子.镜子的长与宽的比是2∶1.已知镜面玻
璃的价格是每平方米120元,边框的价格是每米20元,另外制作这
面镜子还需加工费45元.设制作这面镜子的总费用是y元,镜子的
宽度是x米.
(1)求y与x之间的关系式;
(2)如果制作这面镜子共花了195元,求这面镜子的长和宽. 特别提醒:注意自变量在实际问题中的实际意义,准确确定自变
量的取值范围.【规范解答】(1)y=240x2+120x+45;………………………2分
(2)由题意可得
240x2+120x+45=195,整理得8x2+4x-5=0.…………………5分
解得x1= (舍去).………………………7分
…………………………………8分
答:镜子的长和宽分别是 米和 米.……9分【互动探究】
1.根据实际问题列出二次函数的关系式的关键是什么?
提示:解决问题的关键是找出实际问题中的等量关系,特别是函
数y与自变量x之间的等量关系.2.实际问题中常见的二次函数关系有哪些?
提示:(1)面积、体积的一些计算公式在特定的情况下可以看作
二次函数关系式;
(2)一些物理学公式也满足二次函数关系;
(3)在特定情况下利润和售价的关系等.【规律总结】
建立实际问题中的二次函数关系式的四个步骤
1.认真审题,明确一些关键词的意义.
2.弄清题目中自变量与因变量的意义.
3.找出题目中共有几个条件,每个条件和变量之间可以列出有什
么意义的代数式.
4.确定等量关系,列出函数关系式.【跟踪训练】
4.进入夏季后,某电器商场为了减少库存,对电热取暖器连续进
行两次降价.若设平均每次降价的百分率是x,降价后的价格为y
元,原价为a元,则y与x之间的函数关系式为( )
(A)y=2a(x-1) (B)y=2a(1-x)
(C)y=a(1-x2) (D)y=a(1-x)2
【解析】选D.由题意知第二次降价后的价格是a(1-x)2,则函数
关系式是y=a(1-x)2. 【变式训练】在半径为4 cm的圆中,挖去一个半径为x cm的圆面,
剩下一个圆环的面积为y cm2,则y与x的函数关系式为( )
(A)y=πx2-4 (B)y=π(2-x)2
(C)y=-(x2+4) (D)y=-πx2+16π
【解析】选D.半径为4的圆的面积为16π,
半径为x的圆的面积πx2,
因而函数关系式是y=-πx2+16π. 5.写出下列函数关系式(不必写出自变量的取值范围):
(1)等腰三角形顶角y与底角x之间的函数关系式为________.
(2)汽车油箱中原有油100升,汽车每行驶50千米耗油9升,油箱
中剩余油量y(升)与汽车行驶路程x(千米)之间的函数关系式为
______________.
(3)矩形的周长为30,则面积y与一条边长x之间的函数关系式为
_________.在上述各式中, _________是一次函数,________是
二次函数(只填序号).【解析】(1)由三角形的内角和为180°,
得2x+y=180,即y=180-2x.
(2)∵汽车每行驶50千米耗油9升,
则行驶x千米耗油量为 升,
∴油箱中剩余油量y(升)与汽车行驶路程x(千米)之间的函数关
系式为y=100-(3)∵矩形的周长为30,一边长为x,则另一边的长为15-x,
∴面积y与一条边长x之间的关系式为y=(15-x)x=-x2+15x.
三个式子中(1)(2)是一次函数,(3)是二次函数.
答案:y=180-2x y=100- y=-x2+15x
(1)(2) (3)6.圆的半径为3,若半径增加x,则面积增加y.求y与x的函数关系
式.
【解析】由题意得:y=π(x+3)2-9π,
即y=πx2+6πx(x>0).1.下列函数关系中,是二次函数的是( )
(A)在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
(B)当距离一定时,火车行驶的时间t与速度v之间的关系
(C)等边三角形的周长C与边长a之间的关系
(D)圆心角为120°的扇形面积S与半径R之间的关系
【解析】选D.A:y=mx+b,当m≠0时(m是常数),是一次函数,错
误;B:t= 当s≠0时,是反比例函数,错误;C:C=3a,是正比例
函数,错误;D:S= 是二次函数,正确.2.下列函数中,不是二次函数的是( )
(A)y=1-2x2 (B)y=2(x-1)2+4
(C)y= (x-1)(x+4) (D)y=(x-2)2-x2
【解析】选D.A.y=1-2x2=-2x2+1,是二次函数,正确;
B.y=2(x-1)2+4=2x2-4x+6,是二次函数,正确;
C.y= 是二次函数,正确;
D.y=(x-2)2-x2=-4x+4,是一次函数,错误.3.已知y=(a+1)x2+ax是二次函数,那么a的取值范围是_______.
【解析】根据二次函数的定义可得a+1≠0,
即a≠-1.所以a的取值范围是a≠-1.
答案:a≠-14.正方形的边长是3,若边长增加x,则面积增加y,那么y与x的函
数关系式为_________.
【解析】新正方形的边长是(x+3),则y=(x+3)2-32=x2+6x.
答案:y=x2+6x5.如图,某矩形相框长26 cm,宽20 cm,其
四周相框边(图中阴影部分)的宽度相同,
都是x cm,相框内部的面积(指图中较小矩
形的面积)为y cm2.
(1)写出y与x的函数关系式;
(2)若相框内部的面积为280 cm2,求相框边的宽度.【解析】(1)根据题意得,
y=(26-2x)(20-2x)=4x2-92x+520(0<x<10).
(2)根据题意,得4x2-92x+520=280.
解得x1=3,x2=20(不合题意,舍去).
答:相框边的宽度为3 cm.
答:矩形花圃的面积等于______________________________.
2.设矩形花圃垂直于墙的一边AB的长为x m,取一些值,算出矩形
花圃另一边BC的长,进而得出矩形的面积y m2,并将结果填写在
下表空格里.181614108642矩形花圃的长乘以矩形花圃的宽1832425048423218通过填写表格可以发现当x的值为__时,y的值最大,为___.
即在问题1中垂直于墙的一边AB的长为__ m,另一边BC的长为
__ m时,得到的矩形花圃的面积最大.5505103.在问题1中AB(x)是否可以任意取值?x的取值范围是什么?
答:____________________________________.
4.在问题1中,当AB的长(x)确定后,矩形的面积(y)也随之确定,y
是x的_____,它们之间的函数关系式为
y=_________或y=_________.x不能任意取值.x的取值范围是0<x<10x(20-2x)-2x2+20x函数5.在问题2中等量关系是什么?
答:_________________________.
6.问题2中,设每件商品降价x元,该商品每天的利润为y元,则y是
x的______.函数关系式为:y=___________________或者为y=
________________.其中x表示每件商品降价的钱数,最小降价为
__元,最大降价为__元,因此x的取值范围为________.利润=(售价-进价)×销售量(10-x-8)(100+100x)-100x2+100x+200020≤x≤2函数7.二次函数的定义:形如y=_________(a,b,c是常数,a___0)
的函数叫做二次函数,其中x是_______,__是二次项系数,__
是一次项系数,__是常数项.
【点拨】注意二次函数的二次项的系数不为0是二次函数概念的一
部分.ax2+bx+c≠自变量abc【预习思考】1.二次函数要满足的三个条件是什么?
提示:(1)自变量x的最高次数是2;
(2)a≠0;
(3)右边是关于自变量x的整式,自变量x不能出现在分母中或根号
里.2.函数y=(x-3)(x+2)-x2是二次函数吗?
提示:不是.因为函数y=(x-3)(x+2)-x2整理后化为y=-x-6,它是
一次函数,不是二次函数. 二次函数的定义
【例1】已知函数y=(m2+m)xm2-2m+2.
(1)当函数是二次函数时,求m的值;
(2)当函数是一次函数时,求m的值.
【解题探究】
1.在函数y=(m2+m)xm2-2m+2中,自变量x的系数是m2+m,次数是
m2-2m+2. 2.若y=(m2+m)xm2-2m+2为二次函数,则自变量x的系数和次数应分别
等于什么?m的值等于什么?
答:x的系数不为0,即m2+m≠0,解得m≠0且m≠-1;x的次数为2,
即m2-2m+2=2,解得m=0或m=2,所以m=2.3.若y=(m2+m)xm2-2m+2为一次函数,则自变量x的系数和次数应分
别等于什么?m的值又等于什么?
答:x的系数不为0,即m2+m≠0,解得m≠0且m≠-1;x的次数为1,
即m2-2m+2=1,解得m1=m2=1.所以m=1. _______________________________【互动探究】
二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有
什么联系?
提示:如果把变量y换成一个常数,那么二次函数就是一个一元
二次方程了.【规律总结】
判断二次函数的三步法【跟踪训练】
1.下列函数中,是二次函数的是( )
(A)y=8x2+1 (B)y=8x+1
(C)y= (D)y= +1
【解析】选A.A:符合二次函数的y=ax2+bx+c(a≠0)的形式,是
二次函数,正确;B:是一次函数,错误;C:是反比例函数,错误;
D:自变量x在分母中,不是二次函数,错误.2.若函数y=(m-4)x3m2-2m-3是二次函数,求m的值.
【解析】根据题意得
解得
∴m=-1或m= 实际问题中的二次函数关系
【例2】(9分)在一块长方形镜面玻璃的四周镶上与它的周长相
等的边框,制成一面镜子.镜子的长与宽的比是2∶1.已知镜面玻
璃的价格是每平方米120元,边框的价格是每米20元,另外制作这
面镜子还需加工费45元.设制作这面镜子的总费用是y元,镜子的
宽度是x米.
(1)求y与x之间的关系式;
(2)如果制作这面镜子共花了195元,求这面镜子的长和宽. 特别提醒:注意自变量在实际问题中的实际意义,准确确定自变
量的取值范围.【规范解答】(1)y=240x2+120x+45;………………………2分
(2)由题意可得
240x2+120x+45=195,整理得8x2+4x-5=0.…………………5分
解得x1= (舍去).………………………7分
…………………………………8分
答:镜子的长和宽分别是 米和 米.……9分【互动探究】
1.根据实际问题列出二次函数的关系式的关键是什么?
提示:解决问题的关键是找出实际问题中的等量关系,特别是函
数y与自变量x之间的等量关系.2.实际问题中常见的二次函数关系有哪些?
提示:(1)面积、体积的一些计算公式在特定的情况下可以看作
二次函数关系式;
(2)一些物理学公式也满足二次函数关系;
(3)在特定情况下利润和售价的关系等.【规律总结】
建立实际问题中的二次函数关系式的四个步骤
1.认真审题,明确一些关键词的意义.
2.弄清题目中自变量与因变量的意义.
3.找出题目中共有几个条件,每个条件和变量之间可以列出有什
么意义的代数式.
4.确定等量关系,列出函数关系式.【跟踪训练】
4.进入夏季后,某电器商场为了减少库存,对电热取暖器连续进
行两次降价.若设平均每次降价的百分率是x,降价后的价格为y
元,原价为a元,则y与x之间的函数关系式为( )
(A)y=2a(x-1) (B)y=2a(1-x)
(C)y=a(1-x2) (D)y=a(1-x)2
【解析】选D.由题意知第二次降价后的价格是a(1-x)2,则函数
关系式是y=a(1-x)2. 【变式训练】在半径为4 cm的圆中,挖去一个半径为x cm的圆面,
剩下一个圆环的面积为y cm2,则y与x的函数关系式为( )
(A)y=πx2-4 (B)y=π(2-x)2
(C)y=-(x2+4) (D)y=-πx2+16π
【解析】选D.半径为4的圆的面积为16π,
半径为x的圆的面积πx2,
因而函数关系式是y=-πx2+16π. 5.写出下列函数关系式(不必写出自变量的取值范围):
(1)等腰三角形顶角y与底角x之间的函数关系式为________.
(2)汽车油箱中原有油100升,汽车每行驶50千米耗油9升,油箱
中剩余油量y(升)与汽车行驶路程x(千米)之间的函数关系式为
______________.
(3)矩形的周长为30,则面积y与一条边长x之间的函数关系式为
_________.在上述各式中, _________是一次函数,________是
二次函数(只填序号).【解析】(1)由三角形的内角和为180°,
得2x+y=180,即y=180-2x.
(2)∵汽车每行驶50千米耗油9升,
则行驶x千米耗油量为 升,
∴油箱中剩余油量y(升)与汽车行驶路程x(千米)之间的函数关
系式为y=100-(3)∵矩形的周长为30,一边长为x,则另一边的长为15-x,
∴面积y与一条边长x之间的关系式为y=(15-x)x=-x2+15x.
三个式子中(1)(2)是一次函数,(3)是二次函数.
答案:y=180-2x y=100- y=-x2+15x
(1)(2) (3)6.圆的半径为3,若半径增加x,则面积增加y.求y与x的函数关系
式.
【解析】由题意得:y=π(x+3)2-9π,
即y=πx2+6πx(x>0).1.下列函数关系中,是二次函数的是( )
(A)在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
(B)当距离一定时,火车行驶的时间t与速度v之间的关系
(C)等边三角形的周长C与边长a之间的关系
(D)圆心角为120°的扇形面积S与半径R之间的关系
【解析】选D.A:y=mx+b,当m≠0时(m是常数),是一次函数,错
误;B:t= 当s≠0时,是反比例函数,错误;C:C=3a,是正比例
函数,错误;D:S= 是二次函数,正确.2.下列函数中,不是二次函数的是( )
(A)y=1-2x2 (B)y=2(x-1)2+4
(C)y= (x-1)(x+4) (D)y=(x-2)2-x2
【解析】选D.A.y=1-2x2=-2x2+1,是二次函数,正确;
B.y=2(x-1)2+4=2x2-4x+6,是二次函数,正确;
C.y= 是二次函数,正确;
D.y=(x-2)2-x2=-4x+4,是一次函数,错误.3.已知y=(a+1)x2+ax是二次函数,那么a的取值范围是_______.
【解析】根据二次函数的定义可得a+1≠0,
即a≠-1.所以a的取值范围是a≠-1.
答案:a≠-14.正方形的边长是3,若边长增加x,则面积增加y,那么y与x的函
数关系式为_________.
【解析】新正方形的边长是(x+3),则y=(x+3)2-32=x2+6x.
答案:y=x2+6x5.如图,某矩形相框长26 cm,宽20 cm,其
四周相框边(图中阴影部分)的宽度相同,
都是x cm,相框内部的面积(指图中较小矩
形的面积)为y cm2.
(1)写出y与x的函数关系式;
(2)若相框内部的面积为280 cm2,求相框边的宽度.【解析】(1)根据题意得,
y=(26-2x)(20-2x)=4x2-92x+520(0<x<10).
(2)根据题意,得4x2-92x+520=280.
解得x1=3,x2=20(不合题意,舍去).
答:相框边的宽度为3 cm.
