人教版数学九年级上册23.3课题学习 图案设计同步练习(含答案解析)
文档属性
| 名称 | 人教版数学九年级上册23.3课题学习 图案设计同步练习(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 241.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览

文档简介
23.3 课题学习 图案设计
1.(2018·山东烟台中考)在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,是中心对称图形但不是轴对称图形的是( )
2.下图是由10把相同的折扇组成的“蝶恋花”(图①)和梅花图案(图②)(图中的折扇无重叠),则梅花图案中的五角星的5个锐角均为( )
A.36° B.42° C.45° D.48°
3.规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,则称此图形为旋转对称图形.下列图形是旋转对称图形,且有一个旋转角为60°的是( )
A.正三角形 B.正方形
C.正六边形 D.正十边形
4.如图所示的图案,至少绕它的中心旋转( )才能与自身重合.
A.45° B.90° C.135° D.180°
5.写出一个既有轴对称性质又有中心对称性质的图形名称: .?
6.如图是两个垃圾回收桶上的图案,分别表示可回收垃圾与不可回收垃圾.请你先找出组成图案的“基本图案”,再分析它们的形成过程.
7.如图,在下列4×3的网格上,分别设计出符合要求的图案,作图要求:由个数相同的白色方块与黑色方块组成一幅图案,即黑、白方块的个数要相同.
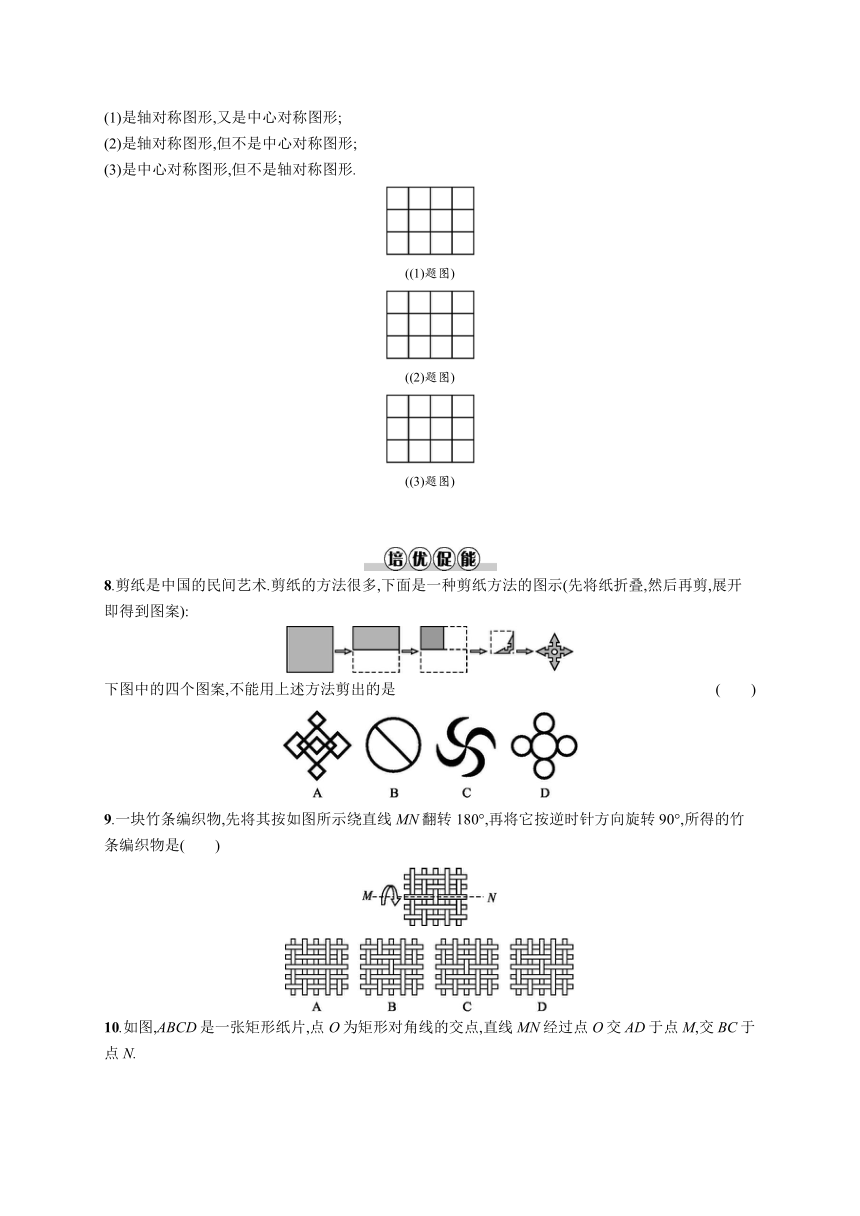
(1)是轴对称图形,又是中心对称图形;
(2)是轴对称图形,但不是中心对称图形;
(3)是中心对称图形,但不是轴对称图形.
((1)题图)
((2)题图)
((3)题图)
8.剪纸是中国的民间艺术.剪纸的方法很多,下面是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案):
下图中的四个图案,不能用上述方法剪出的是 ( )
9.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
10.如图,ABCD是一张矩形纸片,点O为矩形对角线的交点,直线MN经过点O交AD于点M,交BC于点N.
操作:先沿直线MN剪开,并将直角梯形MNCD绕点O旋转 后(填入一个你认为正确答案的序号:①90°;②180°;③270°;④360°),恰与直角梯形NMAB完全重合;再将重合后的直角梯形MNCD以直线MN为轴翻转180°后所得的图形是下图中的 .(填写正确图形的代号)?
★11. 右图所示的是某中学的一块正方形的花坛,现要在里面修两条笔直的小路,使得小路把花坛分成形状相同且面积相等的四部分,在里面种植上不同品种的鲜花.若道路的宽度忽略不计,请你设计3种不同的方案,画图并简略叙述步骤.
12.如图,利用左边所给的基本图形可以设计许多富有生活情趣的图案,如图所示.请你再设计一个图案,并说明它的含义.
★13.为了创建绿色校园,学校决定在一块正方形的空地种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案既是轴对称图形又是中心对称图形.种植花草部分用阴影表示.请你在图③、图④、图⑤中画出3种不同的设计图案.
提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①、图②只能算一种.
课后作业·测评
夯基达标
1.C 2.D
3.C A.正三角形的最小旋转角为120°,本选项错误.B.正方形的最小旋转角为90°,本选项错误.C.正六边形的最小旋转角为60°,本选项正确.D.正十边形的最小旋转角为36°,本选项错误.故选C.
4.A
5.线段、圆、正方形、矩形、菱形、正2n边形(n为正整数)等(写出其中一个即可)
6.解 两个图案都是由相同的“基本图案”——一个“弯曲的箭头”组成的.“可回收垃圾”标志是把一个“弯曲的箭头”向内放置后旋转两次得到的,其中旋转角是120°;“不可回收垃圾”标志是把一个“弯曲的箭头”向外放置后旋转两次得到的,其中旋转角也是120°.
7.解 如图,给出三组答案.
培优促能
8.C 通过剪纸方法的图示可以看出剪出的图案应该既是轴对称图形,又是中心对称图形.在四个图案中,选项C是中心对称图形,但不是轴对称图形.
9.B 10.② (4)
11.分析 本题是方案设计问题,其实质就是利用正方形既是轴对称图形又是中心对称图形这一性质来解决问题.只要两条互相垂直的直线交点落在正方形对角线的交点上,即落在正方形的对称中心上就可以满足要求.
解
12.解 答案不唯一,如下图供参考.
创新应用
13.解 参考答案如下:
1.(2018·山东烟台中考)在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,是中心对称图形但不是轴对称图形的是( )
2.下图是由10把相同的折扇组成的“蝶恋花”(图①)和梅花图案(图②)(图中的折扇无重叠),则梅花图案中的五角星的5个锐角均为( )
A.36° B.42° C.45° D.48°
3.规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,则称此图形为旋转对称图形.下列图形是旋转对称图形,且有一个旋转角为60°的是( )
A.正三角形 B.正方形
C.正六边形 D.正十边形
4.如图所示的图案,至少绕它的中心旋转( )才能与自身重合.
A.45° B.90° C.135° D.180°
5.写出一个既有轴对称性质又有中心对称性质的图形名称: .?
6.如图是两个垃圾回收桶上的图案,分别表示可回收垃圾与不可回收垃圾.请你先找出组成图案的“基本图案”,再分析它们的形成过程.
7.如图,在下列4×3的网格上,分别设计出符合要求的图案,作图要求:由个数相同的白色方块与黑色方块组成一幅图案,即黑、白方块的个数要相同.
(1)是轴对称图形,又是中心对称图形;
(2)是轴对称图形,但不是中心对称图形;
(3)是中心对称图形,但不是轴对称图形.
((1)题图)
((2)题图)
((3)题图)
8.剪纸是中国的民间艺术.剪纸的方法很多,下面是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案):
下图中的四个图案,不能用上述方法剪出的是 ( )
9.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
10.如图,ABCD是一张矩形纸片,点O为矩形对角线的交点,直线MN经过点O交AD于点M,交BC于点N.
操作:先沿直线MN剪开,并将直角梯形MNCD绕点O旋转 后(填入一个你认为正确答案的序号:①90°;②180°;③270°;④360°),恰与直角梯形NMAB完全重合;再将重合后的直角梯形MNCD以直线MN为轴翻转180°后所得的图形是下图中的 .(填写正确图形的代号)?
★11. 右图所示的是某中学的一块正方形的花坛,现要在里面修两条笔直的小路,使得小路把花坛分成形状相同且面积相等的四部分,在里面种植上不同品种的鲜花.若道路的宽度忽略不计,请你设计3种不同的方案,画图并简略叙述步骤.
12.如图,利用左边所给的基本图形可以设计许多富有生活情趣的图案,如图所示.请你再设计一个图案,并说明它的含义.
★13.为了创建绿色校园,学校决定在一块正方形的空地种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案既是轴对称图形又是中心对称图形.种植花草部分用阴影表示.请你在图③、图④、图⑤中画出3种不同的设计图案.
提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①、图②只能算一种.
课后作业·测评
夯基达标
1.C 2.D
3.C A.正三角形的最小旋转角为120°,本选项错误.B.正方形的最小旋转角为90°,本选项错误.C.正六边形的最小旋转角为60°,本选项正确.D.正十边形的最小旋转角为36°,本选项错误.故选C.
4.A
5.线段、圆、正方形、矩形、菱形、正2n边形(n为正整数)等(写出其中一个即可)
6.解 两个图案都是由相同的“基本图案”——一个“弯曲的箭头”组成的.“可回收垃圾”标志是把一个“弯曲的箭头”向内放置后旋转两次得到的,其中旋转角是120°;“不可回收垃圾”标志是把一个“弯曲的箭头”向外放置后旋转两次得到的,其中旋转角也是120°.
7.解 如图,给出三组答案.
培优促能
8.C 通过剪纸方法的图示可以看出剪出的图案应该既是轴对称图形,又是中心对称图形.在四个图案中,选项C是中心对称图形,但不是轴对称图形.
9.B 10.② (4)
11.分析 本题是方案设计问题,其实质就是利用正方形既是轴对称图形又是中心对称图形这一性质来解决问题.只要两条互相垂直的直线交点落在正方形对角线的交点上,即落在正方形的对称中心上就可以满足要求.
解
12.解 答案不唯一,如下图供参考.
创新应用
13.解 参考答案如下:
同课章节目录
