苏科版数学七年级下册专题复习:三角形与多边形课件 (20张PPT)
文档属性
| 名称 | 苏科版数学七年级下册专题复习:三角形与多边形课件 (20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
专题:三角形与多边形
苏科版七年级下册 数学
1.三角形的三线注意点 (1)三角形有三条中线,有三条高线,有三条角平分线,它们都是线段.
(2)锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.
2.三角形的面积 (1)三角形的面积等于底边长与高线乘积的一半,即S△= ×底×高. (2)三角形的中线将三角形分成面积相等的两部分.
1
2
知识回顾
3.多边形的内角和公式:180°(n-2),多边形的外角和是360°.
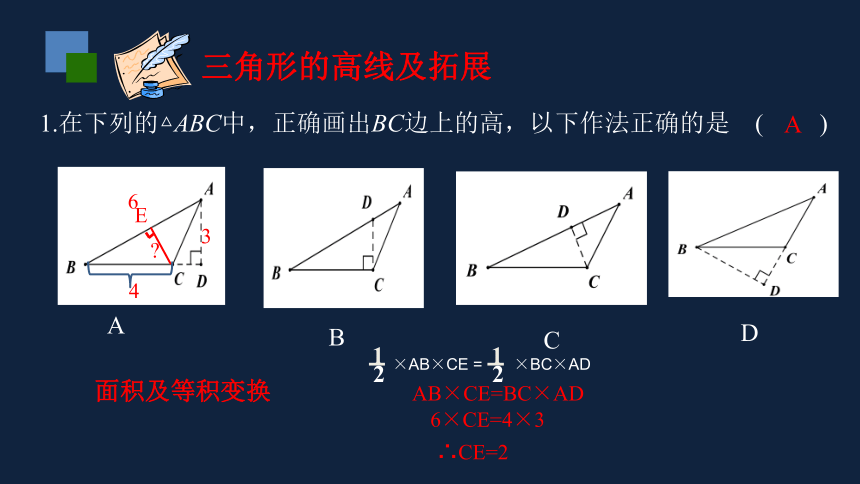
1.在下列的△ABC中,正确画出BC边上的高,以下作法正确的是 ( )
A
A
B
C
D
三角形的高线及拓展
面积及等积变换
E
1
2
×AB×CE = ×BC×AD
1
2
AB×CE=BC×AD
6
4
3
?
6×CE=4×3
∴CE=2
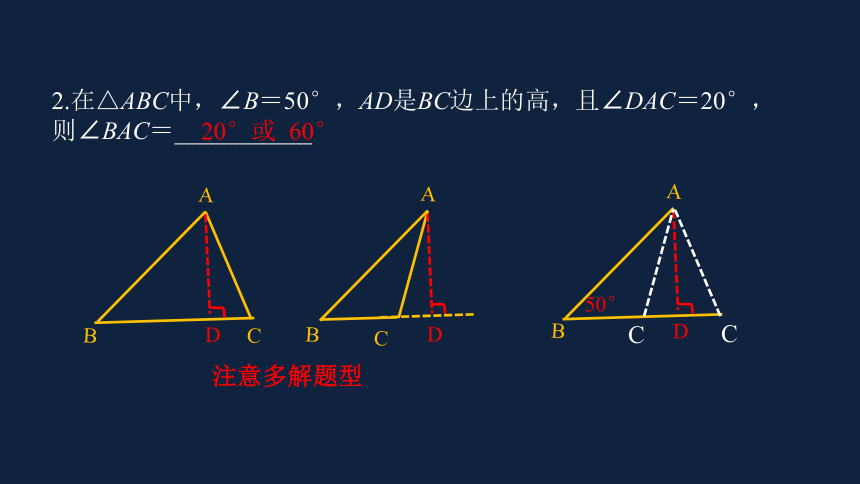
2.在△ABC中,∠B=50°,AD是BC边上的高,且∠DAC=20°,
则∠BAC=___________
A
B
C
D
A
B
C
D
20°或 60°
注意多解题型
A
B
50°
D
C
C
三角形的中线及拓展
1.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为40cm2,则△BEF的面积是_____cm2.
A
B
C
E
F
D
解∵点E是AD的中点,
∴S△ABE= S△ABD ,S△ACE= S△ADC ,
∴S△ABE+S△ACE= S△ABC= ×40=20cm2,
∴S△BCE= S△ABC= ×40=20cm2,
∵点F是CE的中点, ∴S△BEF= S△BCE= ×20=10cm2.
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
10
三角形的中线平分面积
2.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=6,则S1-S2=_________。
A
B
C
D
E
F
1
三角形的中线平分三角形的面积,
同高的两个三角形的面积之比等于其底之比.
解∵BE=CE ∴S△ABE= S△ABD=3
∵AD=2BD∴S△BCD= S△ABD=2
∵S1-S2=S△ABE-S△BCD
∴S1-S2 =3-2=1
1
2
1
3
分析:将△ADF加上四边形BDFE补成△ABE,△CEF加上四边形BDFE补成△BCD.
A
P
B
C
三角形的角平分线及拓展
1 (1).如图,在△ABC中,∠A=80°,
若点P为∠ABC和外角∠ACD的平
分线的交点,则∠P= ;
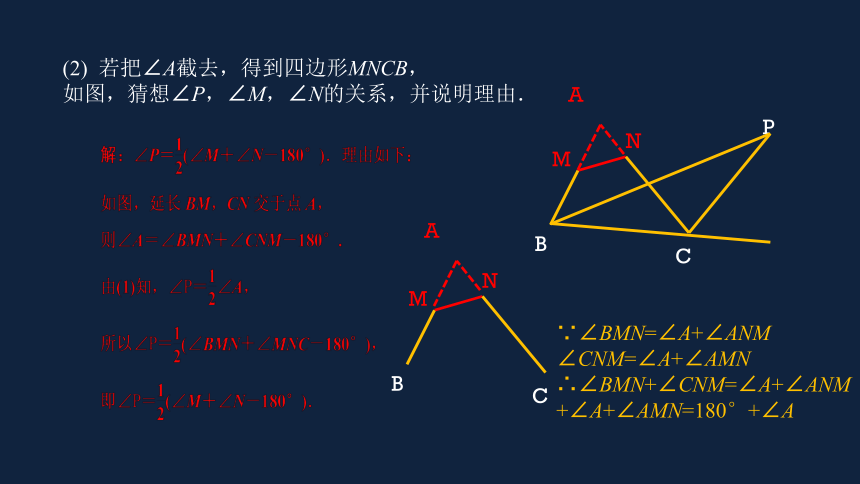
(2) 若把∠A截去,得到四边形MNCB,
如图,猜想∠P,∠M,∠N的关系,
并说明理由.
B
C
M
N
P
40°
解∵P为∠ABC和外角∠ACD的平分线的交点
∴设∠ABP=∠CBP= x,∠ACP=∠MCP= y,
∵∠ACM=∠ABC+∠A
即 2y-2x=80°∴y-x=40°
∵∠PCD=∠PBC+∠P ∴ ∠P = y-x=40°
D
∠BPC= ∠A
1
2
x
x
y
y
(2) 若把∠A截去,得到四边形MNCB,
如图,猜想∠P,∠M,∠N的关系,并说明理由.
P
B
C
M
N
A
∵∠BMN=∠A+∠ANM
∠CNM=∠A+∠AMN
∴∠BMN+∠CNM=∠A+∠ANM
+∠A+∠AMN=180°+∠A
B
C
M
N
A
“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图中∠A+∠B+∠C+∠D+∠E的度数;
∵∠1=∠2+∠D
而∠2=∠B+∠E
∠1=∠B+∠E+∠D,
∵∠1+∠A+∠C=180° ∴∠A+∠B+∠C+∠D+∠E=180°
A
B
C
D
E
1
2
A
B
C
D
E
法一:
法二:
∵∠3=∠B+∠E ,∠3=∠1+∠2
∴∠B+∠E = ∠1+∠2
在△ACD中,
∠A+∠ACD+∠ADC=180°
即∠A+∠B+∠C+∠D+∠E=180°
A
B
C
D
E
1
2
3
B
C
D
1
2
3
A
B
C
D
E
F
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
解∵∠1=∠2+∠F
而∠2=∠B+∠E
∴∠1=∠B+∠E+∠F
在四边形ACDO中,
∵∠1+∠A+∠C+∠D=360°, ∴∠A+∠B+∠C+∠D+∠E+∠F=360°
1
2
O
A
N
B
C
D
E
F
G
M
H
(3)若再对图(2)中的角进一步截去,你能
由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N
的度数吗?只要写出结论,不需要写出解题过程)
分析:根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,所以当截去5个角时增加了180×5度, 则A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
三角形与多边形的联系
知识梳理
三角形
边
角
要素
分类
不等边
三角形
等腰
三角形
锐角
三角形
直角
三角形
钝角
三角形
角平分线
中 线
高
两边之和大于第三边
内角和180°
多边形
三角形
转化
你的收获是什么……
如图,AD是△ABC边BC上的中线,则S△ABD=S△ACD = S△ABC
S△ACD= CD×AH
A
B
C
D
∴S△ABD=S△ACD = S△ABC
理由:∵AD是△ABC边BC上的中线 ∴BD=CD 又∵S△ABD= BD×AH
∴三角形中线平分三角形的面积
1
2
1
2
1
2
小贴士1
1
2
H
如图,△ABC中,DC= 2BD,则 S△ACD=2S△ABD
S△ABD= BD×AH
A
B
C
D
∴S△ACD=2S△ABC
理由: ∵S△ACD= CD×AH
小贴士2
又∵DC= 2BD
1
2
1
2
H
同高的两个三角形的面积之比等于其底之比.
B
C
D
1
2
3
E
∵∠3=∠B+∠E ,
∠3=∠1+∠2
∴∠B+∠E = ∠1+∠2
小贴士3
课后作业:1.好学的小红在学完三角形的角平分线后,钻研了下列几个问题,请你一起参与,共同进步. 如图,△ABC,点 I 是∠ABC与∠ACB平分线的交点,
问题(1):若∠BAC=50°,则∠BIC= °
∠BDC= °
C
A
B
I
M
N
问题(2):△ABC的外角平分线CE交BI的延长线于点E,若∠BAC=x°(0<x<90),则
当∠ACB等于 _____ 度(用含x的代数式表示)时,
CE∥AB.说明理由.
E
G
C
A
B
I
M
N
E
G
问题(3):若△BDE中存在一个内角等于另一个
内角的三倍,试求∠BAC的度数.
如图,△ABC,点 I 是∠ABC与∠ACB平分线的交点,
△ABC的外角平分线CE交BI的延长线于点E,
若∠MBG的平分线BD交CE的反向延长线于点D
D
2.在正方形网格中 , 每个小正方形的边长都为1个
单位长度 , △ABC的三个顶点的位置如图所示,
(1)在图中画出△ABC的AB边上的高线CG
(保留利用格点的作图痕迹);
(2)△ABC的面积为______;
(3)若AB的长为5,AB边上的高是___.
课后作业:
G
1.阅读本章教材;
2.体会数学方法;
3.完成课后思考题。
感谢大家
专题:三角形与多边形
苏科版七年级下册 数学
1.三角形的三线注意点 (1)三角形有三条中线,有三条高线,有三条角平分线,它们都是线段.
(2)锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.
2.三角形的面积 (1)三角形的面积等于底边长与高线乘积的一半,即S△= ×底×高. (2)三角形的中线将三角形分成面积相等的两部分.
1
2
知识回顾
3.多边形的内角和公式:180°(n-2),多边形的外角和是360°.
1.在下列的△ABC中,正确画出BC边上的高,以下作法正确的是 ( )
A
A
B
C
D
三角形的高线及拓展
面积及等积变换
E
1
2
×AB×CE = ×BC×AD
1
2
AB×CE=BC×AD
6
4
3
?
6×CE=4×3
∴CE=2
2.在△ABC中,∠B=50°,AD是BC边上的高,且∠DAC=20°,
则∠BAC=___________
A
B
C
D
A
B
C
D
20°或 60°
注意多解题型
A
B
50°
D
C
C
三角形的中线及拓展
1.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为40cm2,则△BEF的面积是_____cm2.
A
B
C
E
F
D
解∵点E是AD的中点,
∴S△ABE= S△ABD ,S△ACE= S△ADC ,
∴S△ABE+S△ACE= S△ABC= ×40=20cm2,
∴S△BCE= S△ABC= ×40=20cm2,
∵点F是CE的中点, ∴S△BEF= S△BCE= ×20=10cm2.
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
10
三角形的中线平分面积
2.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=6,则S1-S2=_________。
A
B
C
D
E
F
1
三角形的中线平分三角形的面积,
同高的两个三角形的面积之比等于其底之比.
解∵BE=CE ∴S△ABE= S△ABD=3
∵AD=2BD∴S△BCD= S△ABD=2
∵S1-S2=S△ABE-S△BCD
∴S1-S2 =3-2=1
1
2
1
3
分析:将△ADF加上四边形BDFE补成△ABE,△CEF加上四边形BDFE补成△BCD.
A
P
B
C
三角形的角平分线及拓展
1 (1).如图,在△ABC中,∠A=80°,
若点P为∠ABC和外角∠ACD的平
分线的交点,则∠P= ;
(2) 若把∠A截去,得到四边形MNCB,
如图,猜想∠P,∠M,∠N的关系,
并说明理由.
B
C
M
N
P
40°
解∵P为∠ABC和外角∠ACD的平分线的交点
∴设∠ABP=∠CBP= x,∠ACP=∠MCP= y,
∵∠ACM=∠ABC+∠A
即 2y-2x=80°∴y-x=40°
∵∠PCD=∠PBC+∠P ∴ ∠P = y-x=40°
D
∠BPC= ∠A
1
2
x
x
y
y
(2) 若把∠A截去,得到四边形MNCB,
如图,猜想∠P,∠M,∠N的关系,并说明理由.
P
B
C
M
N
A
∵∠BMN=∠A+∠ANM
∠CNM=∠A+∠AMN
∴∠BMN+∠CNM=∠A+∠ANM
+∠A+∠AMN=180°+∠A
B
C
M
N
A
“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图中∠A+∠B+∠C+∠D+∠E的度数;
∵∠1=∠2+∠D
而∠2=∠B+∠E
∠1=∠B+∠E+∠D,
∵∠1+∠A+∠C=180° ∴∠A+∠B+∠C+∠D+∠E=180°
A
B
C
D
E
1
2
A
B
C
D
E
法一:
法二:
∵∠3=∠B+∠E ,∠3=∠1+∠2
∴∠B+∠E = ∠1+∠2
在△ACD中,
∠A+∠ACD+∠ADC=180°
即∠A+∠B+∠C+∠D+∠E=180°
A
B
C
D
E
1
2
3
B
C
D
1
2
3
A
B
C
D
E
F
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
解∵∠1=∠2+∠F
而∠2=∠B+∠E
∴∠1=∠B+∠E+∠F
在四边形ACDO中,
∵∠1+∠A+∠C+∠D=360°, ∴∠A+∠B+∠C+∠D+∠E+∠F=360°
1
2
O
A
N
B
C
D
E
F
G
M
H
(3)若再对图(2)中的角进一步截去,你能
由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N
的度数吗?只要写出结论,不需要写出解题过程)
分析:根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,所以当截去5个角时增加了180×5度, 则A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
三角形与多边形的联系
知识梳理
三角形
边
角
要素
分类
不等边
三角形
等腰
三角形
锐角
三角形
直角
三角形
钝角
三角形
角平分线
中 线
高
两边之和大于第三边
内角和180°
多边形
三角形
转化
你的收获是什么……
如图,AD是△ABC边BC上的中线,则S△ABD=S△ACD = S△ABC
S△ACD= CD×AH
A
B
C
D
∴S△ABD=S△ACD = S△ABC
理由:∵AD是△ABC边BC上的中线 ∴BD=CD 又∵S△ABD= BD×AH
∴三角形中线平分三角形的面积
1
2
1
2
1
2
小贴士1
1
2
H
如图,△ABC中,DC= 2BD,则 S△ACD=2S△ABD
S△ABD= BD×AH
A
B
C
D
∴S△ACD=2S△ABC
理由: ∵S△ACD= CD×AH
小贴士2
又∵DC= 2BD
1
2
1
2
H
同高的两个三角形的面积之比等于其底之比.
B
C
D
1
2
3
E
∵∠3=∠B+∠E ,
∠3=∠1+∠2
∴∠B+∠E = ∠1+∠2
小贴士3
课后作业:1.好学的小红在学完三角形的角平分线后,钻研了下列几个问题,请你一起参与,共同进步. 如图,△ABC,点 I 是∠ABC与∠ACB平分线的交点,
问题(1):若∠BAC=50°,则∠BIC= °
∠BDC= °
C
A
B
I
M
N
问题(2):△ABC的外角平分线CE交BI的延长线于点E,若∠BAC=x°(0<x<90),则
当∠ACB等于 _____ 度(用含x的代数式表示)时,
CE∥AB.说明理由.
E
G
C
A
B
I
M
N
E
G
问题(3):若△BDE中存在一个内角等于另一个
内角的三倍,试求∠BAC的度数.
如图,△ABC,点 I 是∠ABC与∠ACB平分线的交点,
△ABC的外角平分线CE交BI的延长线于点E,
若∠MBG的平分线BD交CE的反向延长线于点D
D
2.在正方形网格中 , 每个小正方形的边长都为1个
单位长度 , △ABC的三个顶点的位置如图所示,
(1)在图中画出△ABC的AB边上的高线CG
(保留利用格点的作图痕迹);
(2)△ABC的面积为______;
(3)若AB的长为5,AB边上的高是___.
课后作业:
G
1.阅读本章教材;
2.体会数学方法;
3.完成课后思考题。
感谢大家
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
