北师大版九年级数学下册课件:1.4 解直角三角形(22张)
文档属性
| 名称 | 北师大版九年级数学下册课件:1.4 解直角三角形(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 15:33:03 | ||
图片预览








文档简介
课件22张PPT。1.4 解直角三角形第一章 直角三角形的边角关系1.掌握解直角三角形的概念;(重点)
2.掌握解直角三角形的依据并能熟练解题.
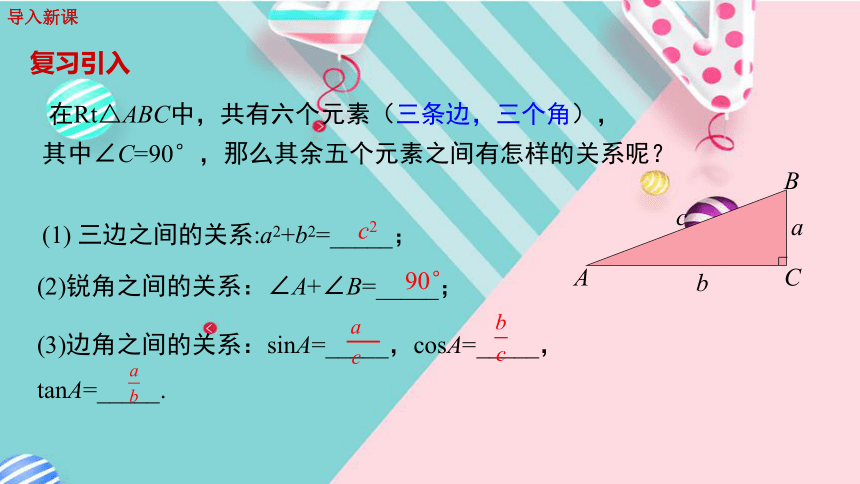
(重点、难点)学习目标(1) 三边之间的关系:a2+b2=_____;(2)锐角之间的关系:∠A+∠B=_____;(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____. 在Rt△ABC中,共有六个元素(三条边,三个角),
其中∠C=90°,那么其余五个元素之间有怎样的关系呢?c290°导入新课复习引入讲授新课问题1 如果已知Rt△ABC中两边的长,你能求出这个三角形其他的元素吗?已知两边解直角三角形例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.解:在Rt△ABC中,a2+b2=c2,在Rt△ABC中,典例精析在如图的Rt△ABC中,根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?ABC62.4练一练问题2 如果已知Rt△ABC中一边和一锐角,你能求出这个三角形其他的元素吗?已知一边及一锐角解直角三角形例2 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C
所对的边分别为a,b,c,∠B=35°,b=20,
求这个直角三角形的其他元素(结果保留小数点后一位).解: 在图中的Rt△ABC中,根据∠A=75°,斜边AB=6,
你能求出这个直角三角形的其他元素吗?ABC675°)练一练 事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素. 由直角三角形中已知的元素,求出所有未知元素的过程,
叫做解直角三角形.归纳总结例3 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.D解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +构造直角三角形解决问题 如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
sinB= ,则菱形的周长是( )
A.10 B.20 C.40 D.28 C练一练1.如图,在Rt△ABC中,∠C=90°,∠B=30°,
AB=8,则BC的长是( ) D当堂练习2.在△ABC中,AB=AC=3,BC=4,则cosB 的值是_________.3.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB= ,则AC的长为( )
A.3 B.3.75
C.4.8 D.5 B4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 30 , b = 20 ;解:根据勾股定理得 (2) ∠B=72°,c = 14.解:5. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.6解:∵AD平分∠BAC,6. 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.解:ACB7. 如图,某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为多少米?解:如图所示,依题意可知,当∠B=600 时,答:梯子的长至少4.62米.CAB当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.解:∵cos∠B= ,∴∠B=45°,当△ABC为钝角三角形时,如图①,∵AC=13,∴由勾股定理得CD=5∴BC=BD-CD=12-5=7;∴BC的长为7或17.当三角形的形状不确定时,一定要注意分类讨论.8. 在△ABC中,AB= ,AC=13,cos∠B= ,
求BC的长.
解直角三角形依据解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素勾股定理两锐角互余锐角的三角函数课堂小结(2)两锐角之间的关系∠A+∠B=90°(3)边角之间的关系(1)三边之间的关系 (勾股定理)在解直角三角形的过程中,一般要用到下面一些关系:
2.掌握解直角三角形的依据并能熟练解题.
(重点、难点)学习目标(1) 三边之间的关系:a2+b2=_____;(2)锐角之间的关系:∠A+∠B=_____;(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____. 在Rt△ABC中,共有六个元素(三条边,三个角),
其中∠C=90°,那么其余五个元素之间有怎样的关系呢?c290°导入新课复习引入讲授新课问题1 如果已知Rt△ABC中两边的长,你能求出这个三角形其他的元素吗?已知两边解直角三角形例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.解:在Rt△ABC中,a2+b2=c2,在Rt△ABC中,典例精析在如图的Rt△ABC中,根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?ABC62.4练一练问题2 如果已知Rt△ABC中一边和一锐角,你能求出这个三角形其他的元素吗?已知一边及一锐角解直角三角形例2 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C
所对的边分别为a,b,c,∠B=35°,b=20,
求这个直角三角形的其他元素(结果保留小数点后一位).解: 在图中的Rt△ABC中,根据∠A=75°,斜边AB=6,
你能求出这个直角三角形的其他元素吗?ABC675°)练一练 事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素. 由直角三角形中已知的元素,求出所有未知元素的过程,
叫做解直角三角形.归纳总结例3 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.D解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +构造直角三角形解决问题 如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
sinB= ,则菱形的周长是( )
A.10 B.20 C.40 D.28 C练一练1.如图,在Rt△ABC中,∠C=90°,∠B=30°,
AB=8,则BC的长是( ) D当堂练习2.在△ABC中,AB=AC=3,BC=4,则cosB 的值是_________.3.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB= ,则AC的长为( )
A.3 B.3.75
C.4.8 D.5 B4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 30 , b = 20 ;解:根据勾股定理得 (2) ∠B=72°,c = 14.解:5. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.6解:∵AD平分∠BAC,6. 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.解:ACB7. 如图,某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为多少米?解:如图所示,依题意可知,当∠B=600 时,答:梯子的长至少4.62米.CAB当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.解:∵cos∠B= ,∴∠B=45°,当△ABC为钝角三角形时,如图①,∵AC=13,∴由勾股定理得CD=5∴BC=BD-CD=12-5=7;∴BC的长为7或17.当三角形的形状不确定时,一定要注意分类讨论.8. 在△ABC中,AB= ,AC=13,cos∠B= ,
求BC的长.
解直角三角形依据解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素勾股定理两锐角互余锐角的三角函数课堂小结(2)两锐角之间的关系∠A+∠B=90°(3)边角之间的关系(1)三边之间的关系 (勾股定理)在解直角三角形的过程中,一般要用到下面一些关系:
