华东师大版八年级下册数学 20.3 数据的离散程度 同步练习(解析版)
文档属性
| 名称 | 华东师大版八年级下册数学 20.3 数据的离散程度 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 83.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览


文档简介
20.3 数据的离散程度 同步练习
一.选择题
1.已知一组数据2,l,,7,3,5,3,2的众数是2,则这组数据的中位数是( ).
A.2 B.2.5 C.3 D.5
2.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,,81,这组成绩的平均数是77,则的值为( ).
A.76 B.75 C.74 D.73
3.有8个数的平均数是11,还有12个数的平均数是12,则这20个数的平均数是( ).
A.11.6 B.232 C.23.2 D.11.5
4.济南某中学足球队的18名队员的年龄如表所示:
年龄(单位:岁) 12 13 14 15
人数 3 5 6 4
这18名队员年龄的众数和中位数分别是( )
A.13岁,14岁 B.14岁,14岁 C.14岁,13岁 D.14岁,15岁
5. 生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A.1000只 B.10000只 C.5000只 D.50000只
6. 某特警部队为了选拔“神枪手”,举行了1000米射击比赛,最后由甲、乙两名战士进入决赛,在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99.68环,甲的方差是0.28,乙的方差是0.21,则下列说法中,正确的是( )
A.甲的成绩比乙的成绩稳定 B.乙的成绩比甲的成绩稳定
C.甲、乙两人成绩的稳定性相同 D.无法确定谁的成绩更稳定
二.填空题
7.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为________.
8.数据1、2、4、4、3、5、l、4、4、3、2、3、4、5,它们的众数是____、中位数是____、平均数是_______.
9. 给出一组数据:23,22,25,23,27,25,23,则这组数据的中位数是______;方差是______ (精确到0.1).
10.在数据-1,0,4,5,8中插入一个数据,使得该数据组的中位数为3,则=________.
11.一次数学测试,某小组五名同学的成绩如下表(有1个数据被遮盖)
组员 甲 乙 丙 丁 戊 平均成绩
成绩 91 89 ★ 90 92 90
那么这五名同学成绩的方差是 分2.
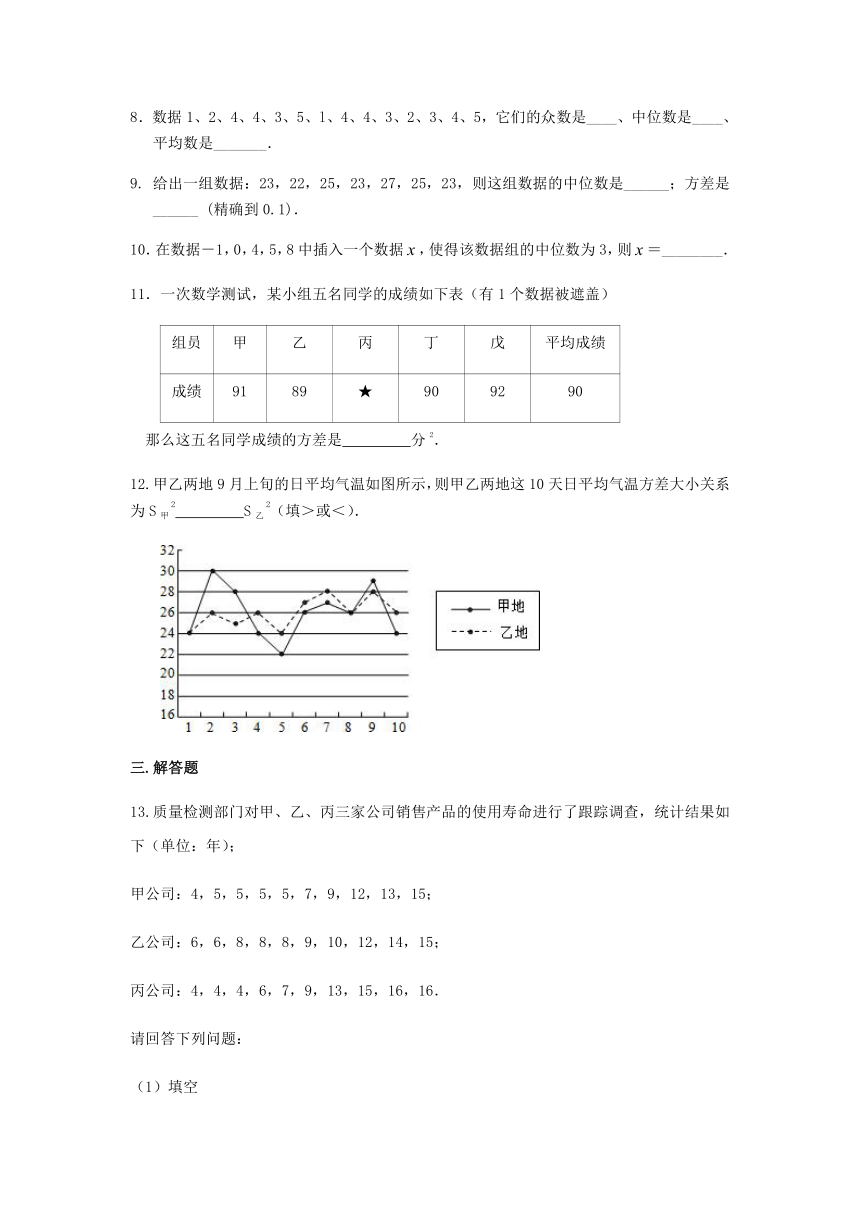
12.甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为S甲2 S乙2(填>或<).
三.解答题
13.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年);
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空
公司数值统计量 平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲公司 5
乙公司 9.6 8.5
丙公司 9.4 4
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
(3)如果你是丙公司的推销员,你将如何结合上述数据及统计量,对本公司的产品进行推销?(至少说两条)
14. 甲、乙两名学生进行射击练习,两人在相同条件下各射10次,将射击结果作统计分析,如下表所示:
命中环数 5 6 7 8 9 10 平均数 众数 方差
甲命中环数的次数 1 4 2 1 1 1 7 6 2.2
乙命中环数的次数 1 2 4 2 1
(1)请你填上表中乙学生的相关数据;
(2)根据你所学的统计知识,利用上述某些数据评价甲、乙两人的射击水平.
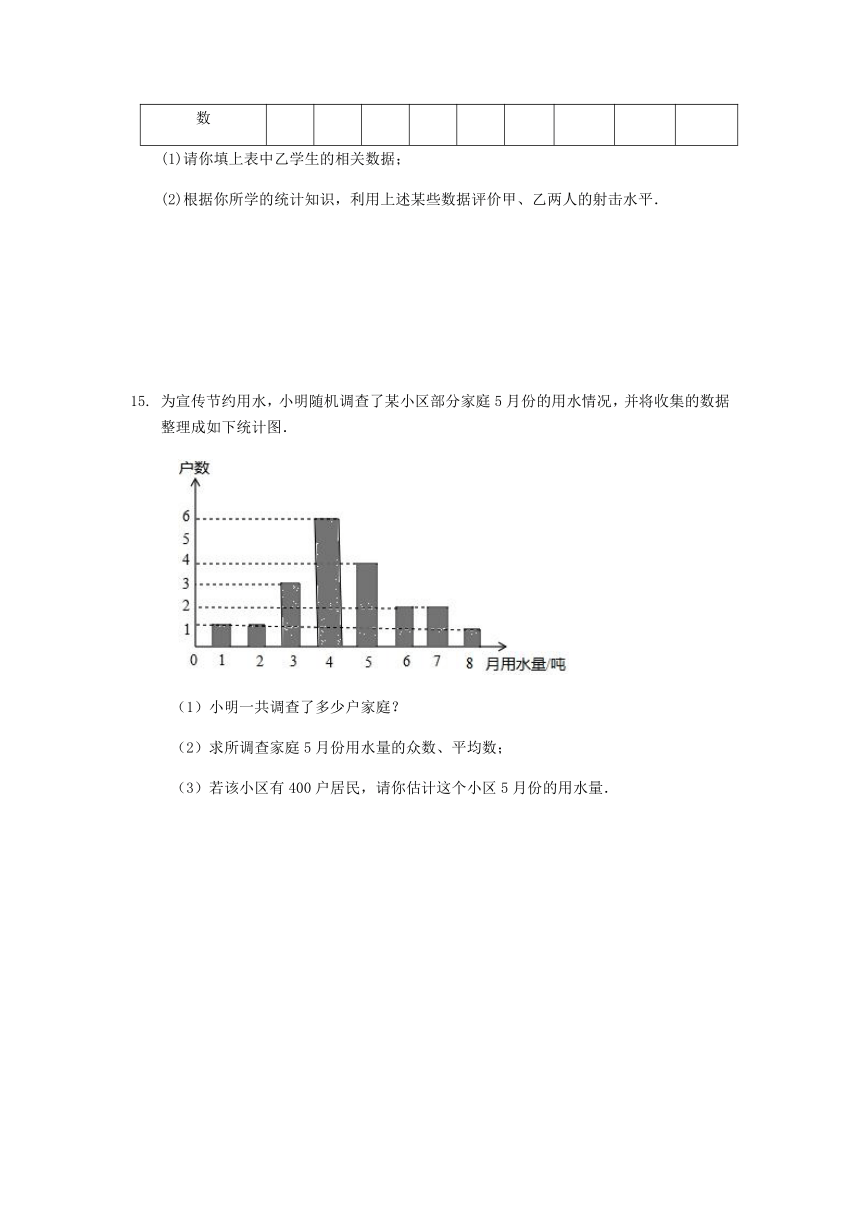
15. 为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数;
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
参考答案
一.选择题
1.【答案】B;
【解析】由众数的意义可知=2,然后按照从小到大的顺序排列这组数据,则中位数应为.
2.【答案】D;
【解析】由题意,解得.
3.【答案】A;
【解析】
4.【答案】B;
【解析】解:∵济南某中学足球队的18名队员中,14岁的最多,有6人,
∴这18名队员年龄的众数是14岁;
∵18÷2=9,第9名和第10名的成绩是中间两个数,
∵这组数据的中间两个数分别是14岁、14岁,
∴这18名队员年龄的中位数是:
(14+14)÷2
=28÷2
=14(岁)
综上,可得这18名队员年龄的众数是14岁,中位数是14岁.
故选:B.
5.【答案】B;
【解析】解:100÷=10000只.故选B.
6.【答案】B;
【解析】解:方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
∵甲的方差是0.28,乙的方差是0.21,
∴乙的成绩比甲的成绩稳定;故选B.
二.填空题
7.【答案】1、3、5或2、3、4
8.【答案】4;3.5;3.21;
【解析】 数据中4出现了5次,出现的次数最多,所以众数是4;把数据重新排列,最中间的两个数是3和4,所以这组数据的中位数是3.5;这组数据的平均数是.
9.【答案】23 2.6;
【解析】先把这组数据按照从小到大的顺序排列,不难发现处于中间的数是23,然后求出平均数是24,再利用公式便可求出方差约为2.6.
10.【答案】2;
11.【答案】2;
【解析】解:根据题意得:
90×5﹣(91+89+90+92)=88,
方差=[(91﹣90)2+(89﹣90)2+(88﹣90)2+(90﹣90)2+(92﹣90)2]=2.
故答案为:2.
12.【答案】>;
【解析】解:观察平均气温统计图可知:乙地的平均气温比较稳定,波动小;
则乙地的日平均气温的方差小,
故S2甲>S2乙.
故答案为:>.
三.解答题
13.【解析】
解:(1)甲厂:平均数为(4+5+5+5+5+7+9+12+13+15)=8,中位数是6;
乙厂:众数为8;
丙厂:中位数为8;
公司数值 平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲公司 8 5 6
乙公司 9.6 8 8.5
丙公司 9.4 4 8
(2)乙公司.因为从平均数、众数和中位数三项指标上看,都比其他的两个公司要好,
他们的产品质量更高.
(3)①丙公司的平均数和中位数都比甲公司高;②以从产品寿命的最高年限考虑,购买丙公司的产品的使用寿命比较高的机会比乙公司产品大一些.
14.【解析】
解:乙命中10环的次数为0;
乙所命中环数的众数为7,其平均数为
;
故其方差为.
甲、乙两人射击水平的评价:①从成绩的平均数与众数看,甲与乙的成绩相差不多;②从成绩的稳定性看,,乙的成绩波动小,比较稳定;③从良好率(成绩在8环或8环以上)看,甲、乙两人成绩相同;④从优秀率看(成绩在9环及9环以上)看,甲的成绩比乙的成绩好.
15.【解析】
解:(1)1+1+3+6+4+2+2+1=20,
答:小明一共调查了20户家庭;
(2)每月用水4吨的户数最多,有6户,故众数为4吨;
平均数:(1×1+1×2+3×3+4×6+5×4+6×2+7×2+8×1)÷20=4.5(吨);
(3)400×4.5=1800(吨),
答:估计这个小区5月份的用水量为1800吨.
