沪科版八上数学第13章13.2.3 三角形内角和定理 习题课件(25张PPT)
文档属性
| 名称 | 沪科版八上数学第13章13.2.3 三角形内角和定理 习题课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览






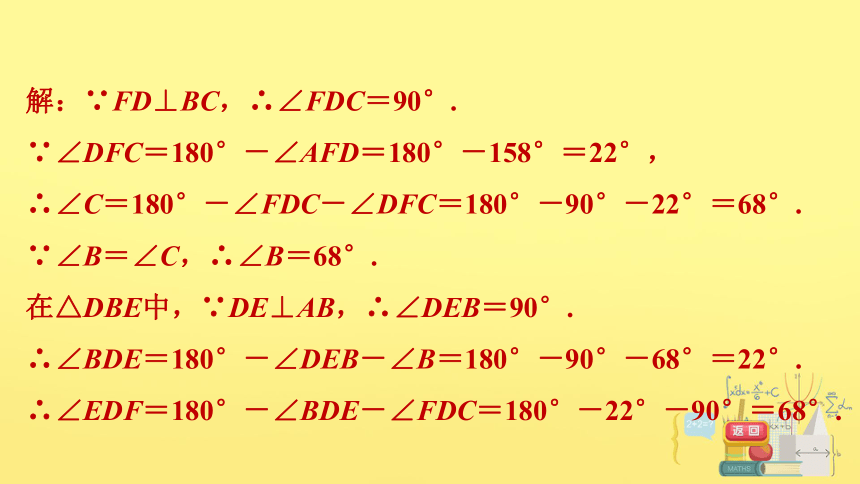
文档简介
(共25张PPT)
13.2 命题与证明
三角形内角和定理
第13章 三角形中的边角关系、命题与证明
答案显示
60°
180°
D
C
105
核心必知
基础巩固练
B
互余
答案显示
A
能力提升练
基础巩固练
B
50°或80°
素养核心练
1.三角形的内角和等于________.
2.直角三角形中,一个锐角的度数为30°,则另一个锐角的度数是________.
3.有两个角________的三角形是直角三角形.
180°
60°
互余
1.在△ABC中,已知∠A=3∠C=54°,则∠B的度数是( )
A.90° B.94°
C.98° D.108°
D
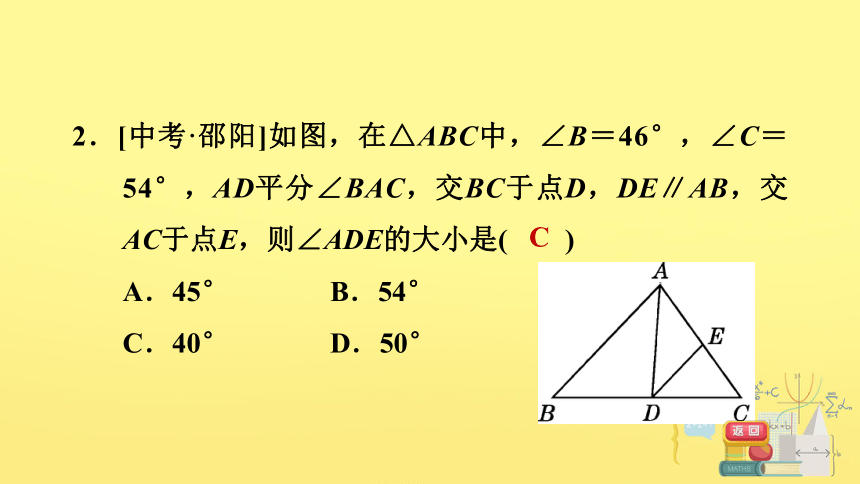
2.[中考·邵阳]如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE的大小是( )
A.45° B.54°
C.40° D.50°
C
3.[2018·合肥包河区期末]一副三角尺按如图所示的方式叠放在一起,则∠α=________度.
105
4.如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,求∠EDF的度数.
解:∵FD⊥BC,∴∠FDC=90°.
∵∠DFC=180°-∠AFD=180°-158°=22°,
∴∠C=180°-∠FDC-∠DFC=180°-90°-22°=68°.
∵∠B=∠C,∴∠B=68°.
在△DBE中,∵DE⊥AB,∴∠DEB=90°.
∴∠BDE=180°-∠DEB-∠B=180°-90°-68°=22°.
∴∠EDF=180°-∠BDE-∠FDC=180°-22°-90°=68°.
5.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
B
6.[中考·遵义]如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )
A.90° B.85°
C.80° D.60°
A
7.[2018·合肥瑶海区期中]如图,已知AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.
解:∵AB∥CD,∠A=37°,
∴∠DCE=∠A=37°.
∵DE⊥AE,∴∠CED=90°.
∴∠D=90°-∠DCE=90°-37°=53°.
8.[阜阳19中月考]如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部点A′处时,∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找出这个规律,你发现的规律是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
【点拨】∵在△ADE中,∠A+∠ADE+∠AED=180°,在△A′DE中,∠A′+∠A′DE+∠A′ED=180°,∴∠A+∠A′+∠ADA′+∠AEA′=360°.∴2∠A+180°-∠2+180°-∠1=360°.∴2∠A=∠1+∠2.故选B.
【答案】B
9.[2019·亳州蒙城一中期中]已知等腰三角形中有一个内角为80°,则该等腰三角形的底角为____________________________.
【点拨】由于不确定80°的角是等腰三角形的底角还是顶角,故应分80°的角是顶角和底角两种情况讨论.
当80°的角为等腰三角形的顶角时,底角的度数=(180°-80°)÷2=50°;当80°的角为等腰三角形的底角时,其底角为80°,故它的底角度数是50°或80°.
【答案】50°或80°
10.如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使∠CAD=∠D,求∠BAD的度数.
解:∵∠ACB=80°,
∴∠ACD=180°-∠ACB=180°-80°=100°.
又∵∠CAD=∠D,∠ACD+∠CAD+∠D=180°,
∴∠CAD=∠D=40°.
在△ABD中,
∠BAD=180°-∠ABD-∠D=180°-46°-40°=94°.
11.如图,在△ABC中,AD是角平分线,∠B=50°,∠C=70°.
(1)求∠ADB的度数;
解:(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C
=180°-50°-70°=60°.
∵AD平分∠BAC,∴∠BAD=∠DAC=30°.
∴∠ADB=180°-∠BAD-∠B=180°-30°-50°=100°.
11.如图,在△ABC中,AD是角平分线,∠B=50°,∠C=70°.
(2)若DE⊥AC,求∠EDC的度数.
解:∵DE⊥AC,∴∠DEC=90°,
∴∠EDC=180°-∠DEC-∠C
=180°-90°-70°=20°.
12.如图,有一艘渔船上午9时在A处沿正东方向航行,在A处测得灯塔C在北偏东60°方向上,渔船行驶2 h到达B处,在B处测得灯塔C在北偏东15°方向上,试求△ABC各内角的度数.
解:由题意可知∠MAC=60°,∠NBC=15°,
所以∠BAC=90°-60°=30°,
∠ABC=90°+15°=105°,
所以∠C=180°-30°-105°=45°.
13.我们知道,三角形三个内角的和是180°,我们可以用对角线(连接多边形任意不相邻的两个顶点的线段叫做多边形的对角线)将多边形分成若干个三角形来计算多边形的内角和.
(1)如图,从四边形的一个顶点可以引出1条对角线,把四边形分成2个三角形; 则四边形的内角和为________;从五边形的一个顶点可以引出2条对角线,把五边形分成________个三角形,则五边形的内角和为________;从六边形的一个顶点可以引出________条对角线,把六边形分成________个三角形,则六边形的内角和为________;
360°
3
540°
3
4
720°
(2)如图,从n边形的一个顶点可以引出________条对角线,把n边形分成________个三角形. n边形的内角和为___________;(用含n的代数式表示)
(3)请根据上面你所找到的规律尝试计算十二边形的内角和.
解:十二边形的内角和为(12-2)×180°=1 800°.
(n-3)
(n-2)
(n-2)·180°
13.2 命题与证明
三角形内角和定理
第13章 三角形中的边角关系、命题与证明
答案显示
60°
180°
D
C
105
核心必知
基础巩固练
B
互余
答案显示
A
能力提升练
基础巩固练
B
50°或80°
素养核心练
1.三角形的内角和等于________.
2.直角三角形中,一个锐角的度数为30°,则另一个锐角的度数是________.
3.有两个角________的三角形是直角三角形.
180°
60°
互余
1.在△ABC中,已知∠A=3∠C=54°,则∠B的度数是( )
A.90° B.94°
C.98° D.108°
D
2.[中考·邵阳]如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE的大小是( )
A.45° B.54°
C.40° D.50°
C
3.[2018·合肥包河区期末]一副三角尺按如图所示的方式叠放在一起,则∠α=________度.
105
4.如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,求∠EDF的度数.
解:∵FD⊥BC,∴∠FDC=90°.
∵∠DFC=180°-∠AFD=180°-158°=22°,
∴∠C=180°-∠FDC-∠DFC=180°-90°-22°=68°.
∵∠B=∠C,∴∠B=68°.
在△DBE中,∵DE⊥AB,∴∠DEB=90°.
∴∠BDE=180°-∠DEB-∠B=180°-90°-68°=22°.
∴∠EDF=180°-∠BDE-∠FDC=180°-22°-90°=68°.
5.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
B
6.[中考·遵义]如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )
A.90° B.85°
C.80° D.60°
A
7.[2018·合肥瑶海区期中]如图,已知AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.
解:∵AB∥CD,∠A=37°,
∴∠DCE=∠A=37°.
∵DE⊥AE,∴∠CED=90°.
∴∠D=90°-∠DCE=90°-37°=53°.
8.[阜阳19中月考]如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部点A′处时,∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找出这个规律,你发现的规律是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
【点拨】∵在△ADE中,∠A+∠ADE+∠AED=180°,在△A′DE中,∠A′+∠A′DE+∠A′ED=180°,∴∠A+∠A′+∠ADA′+∠AEA′=360°.∴2∠A+180°-∠2+180°-∠1=360°.∴2∠A=∠1+∠2.故选B.
【答案】B
9.[2019·亳州蒙城一中期中]已知等腰三角形中有一个内角为80°,则该等腰三角形的底角为____________________________.
【点拨】由于不确定80°的角是等腰三角形的底角还是顶角,故应分80°的角是顶角和底角两种情况讨论.
当80°的角为等腰三角形的顶角时,底角的度数=(180°-80°)÷2=50°;当80°的角为等腰三角形的底角时,其底角为80°,故它的底角度数是50°或80°.
【答案】50°或80°
10.如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使∠CAD=∠D,求∠BAD的度数.
解:∵∠ACB=80°,
∴∠ACD=180°-∠ACB=180°-80°=100°.
又∵∠CAD=∠D,∠ACD+∠CAD+∠D=180°,
∴∠CAD=∠D=40°.
在△ABD中,
∠BAD=180°-∠ABD-∠D=180°-46°-40°=94°.
11.如图,在△ABC中,AD是角平分线,∠B=50°,∠C=70°.
(1)求∠ADB的度数;
解:(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C
=180°-50°-70°=60°.
∵AD平分∠BAC,∴∠BAD=∠DAC=30°.
∴∠ADB=180°-∠BAD-∠B=180°-30°-50°=100°.
11.如图,在△ABC中,AD是角平分线,∠B=50°,∠C=70°.
(2)若DE⊥AC,求∠EDC的度数.
解:∵DE⊥AC,∴∠DEC=90°,
∴∠EDC=180°-∠DEC-∠C
=180°-90°-70°=20°.
12.如图,有一艘渔船上午9时在A处沿正东方向航行,在A处测得灯塔C在北偏东60°方向上,渔船行驶2 h到达B处,在B处测得灯塔C在北偏东15°方向上,试求△ABC各内角的度数.
解:由题意可知∠MAC=60°,∠NBC=15°,
所以∠BAC=90°-60°=30°,
∠ABC=90°+15°=105°,
所以∠C=180°-30°-105°=45°.
13.我们知道,三角形三个内角的和是180°,我们可以用对角线(连接多边形任意不相邻的两个顶点的线段叫做多边形的对角线)将多边形分成若干个三角形来计算多边形的内角和.
(1)如图,从四边形的一个顶点可以引出1条对角线,把四边形分成2个三角形; 则四边形的内角和为________;从五边形的一个顶点可以引出2条对角线,把五边形分成________个三角形,则五边形的内角和为________;从六边形的一个顶点可以引出________条对角线,把六边形分成________个三角形,则六边形的内角和为________;
360°
3
540°
3
4
720°
(2)如图,从n边形的一个顶点可以引出________条对角线,把n边形分成________个三角形. n边形的内角和为___________;(用含n的代数式表示)
(3)请根据上面你所找到的规律尝试计算十二边形的内角和.
解:十二边形的内角和为(12-2)×180°=1 800°.
(n-3)
(n-2)
(n-2)·180°
