沪科版八上数学第13章13.2.4三角形外角的性质习题课件(24张PPT)
文档属性
| 名称 | 沪科版八上数学第13章13.2.4三角形外角的性质习题课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 586.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 15:40:37 | ||
图片预览




文档简介
(共24张PPT)
第13章 三角形中的边角关系、命题与证明
13.2 命题与证明
三角形外角的性质
答案显示
不相邻;大于
延长线;2;相等
D
A
C
A
核心必知
基础巩固练
C
360°
答案显示
能力提升练
基础巩固练
B
101°
∠1>∠2>∠3
C
能力提升练
360
D
1.三角形的一边与另一边的________组成的角,叫三角形的外角;三角形的每个顶点处都有________个外角,且这两个外角________.
2.三角形的外角等于与它________的两个内角的和;因此它________与它不相邻的任一内角.
3.三角形的外角和等于________.
延长线
2
相等
不相邻
大于
360°
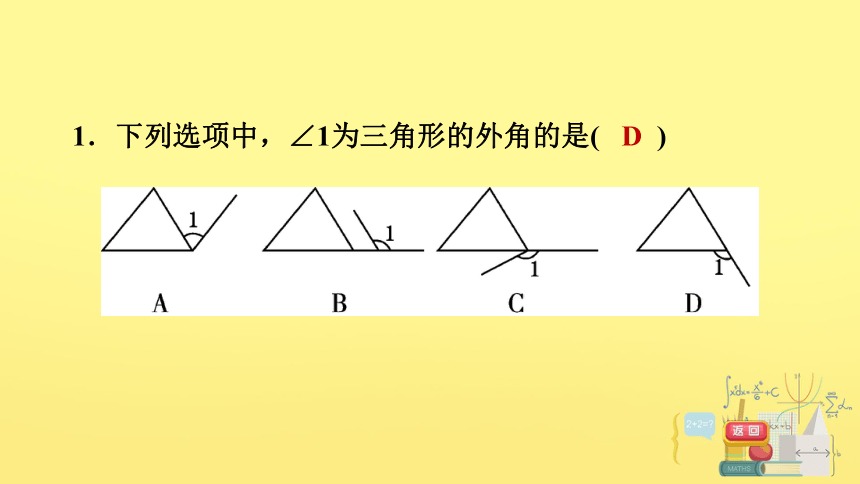
1.下列选项中,∠1为三角形的外角的是( )
D
2.关于三角形的外角,下列说法中错误的是( )
A.一个三角形只有三个外角
B.三角形的每个顶点处都有两个外角
C.三角形的每个外角是与它相邻内角的邻补角
D.一个三角形共有六个外角
A
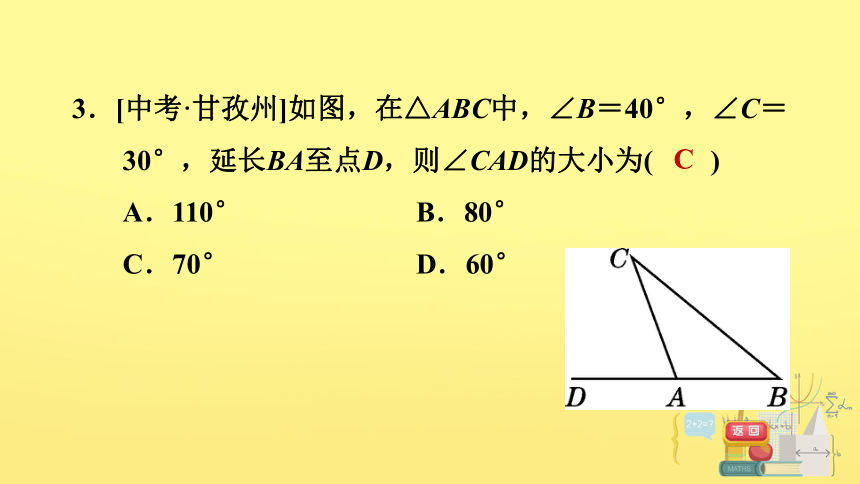
3.[中考·甘孜州]如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
A.110° B.80°
C.70° D.60°
C
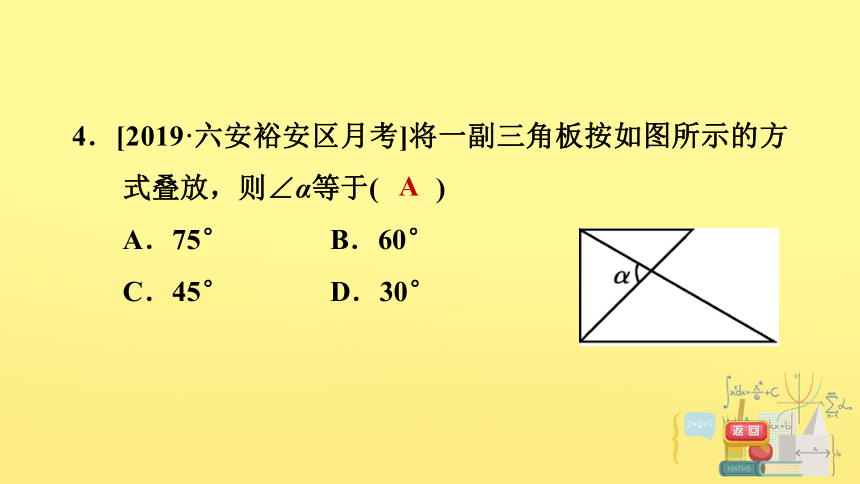
4.[2019·六安裕安区月考]将一副三角板按如图所示的方式叠放,则∠α等于( )
A.75° B.60°
C.45° D.30°
A
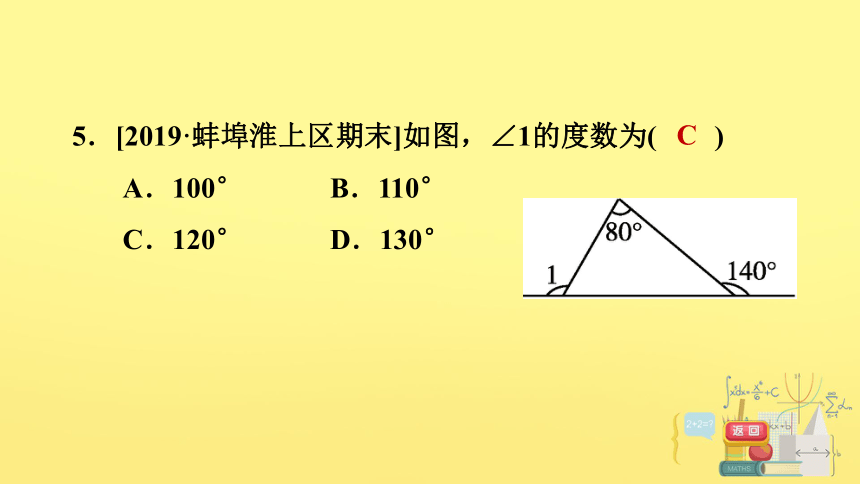
5.[2019·蚌埠淮上区期末]如图,∠1的度数为( )
A.100° B.110°
C.120° D.130°
C
6.[2018·合肥庐阳区期末]如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2=______________.
101°
7.如图,在△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连接EF,则∠1,∠2,∠3的大小关系是____________________.
∠1>∠2>∠3
8.如图,D是△ABC的边BC上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
解:∵∠BAC+∠B+∠C=180°,∠BAC=70°,
∠B=40°,∴∠C=70°.
解:∵∠ADC=∠B+∠BAD=80°,∠B=∠BAD,∴∠B=40°.
9.如图,AD平分∠BAC,∠EAD=∠EDA,那么∠EAC与∠B相等吗?为什么?
解:相等;理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∠EAD=∠EDA,
∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
10.下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
C
11.一块试验田的形状为等边三角形(设其为△ABC),为了了解情况,管理员甲从顶点A出发,沿AB→BC→CA的方向走了一圈回到顶点A处.管理员乙从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到出发点D处.则甲、乙两位管理员从出发到回到原处的途中身体( )
A.甲、乙都转过180°
B.甲、乙都转过360°
C.甲转过120°,乙转过180°
D.甲转过240°,乙转过360°
D
12.[2018·安庆期末]已知直线l1∥l2,一块含30°角的直角三角尺如图所示放置,∠1=25°,则∠2等于( )
A.30° B.35°
C.40° D.45°
B
13.[2018·合肥45中期中]如图,D,E,F分别是△ABC的边BC,AC,AB上的点,则∠1+∠2+∠3+∠4+∠5+∠6=________°.
360
【点拨】设BE和CF交于点N,则∠4=∠ECN+∠ENC.
∵∠ENC=∠FNB,∴∠4=∠ECN+∠FNB.
∵∠5+∠2+∠3+∠ECN=∠1+∠6+∠FNB=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6
=∠1+∠2+∠3+∠ECN+∠FNB+∠5+∠6
=(∠2+∠3+∠5+∠ECN)+(∠1+∠6+∠FNB)
=180°+180°=360°.
14.[2018·合肥瑶海区期末]如图,点D是△ABC的边BC上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.
解:∵∠1=∠2,∠3=∠4,∠4=∠1+∠2,
∴∠3=2∠2.∵∠BAC=66°,
∴∠2+∠3=180°-66°=114°,
即3∠2=114°.∴∠2=38°,∠3=76°.
∴∠DAC=180°-2∠3=180°-2×76°=28°.
15.[2017·阜阳颍州区月考]如图,AD平分∠EAC,交BC的延长线于点D,若∠B=40°,∠ACD=100°,求∠DAE的度数.
16.如图,在△ABC中,∠1=∠2=∠3.
(1)求证:∠BAC=∠DEF;
证明:在△ACE中,∠DEF=∠3+∠CAE,
∵∠1=∠3,∴∠DEF=∠1+∠CAE=∠BAC,
即∠BAC=∠DEF.
16.如图,在△ABC中,∠1=∠2=∠3.
(2)若∠BAC=70°,∠DFE=50°,求∠ABC的度数.
解:在△BCF中,∠DFE=∠2+∠BCF,
∵∠2=∠3,∴∠DFE=∠3+∠BCF,
即∠DFE=∠ACB.
∵∠BAC=70°,∠DFE=50°,
∴∠ABC=180°-∠BAC-∠ACB
=180°-70°-50°=60°.
17.(1)如图①,AC,BD交于点O,连接AD,BC.
求证:∠A+∠D=∠B+∠C;
证明:∵∠AOB是△AOD的外角,
∴∠A+∠D=∠AOB.
∵∠AOB是△BOC的外角,
∴∠B+∠C=∠AOB.
∴∠A+∠D=∠B+∠C.
(2)如图②,利用(1)中结论计算:∠A+∠B+∠C+∠D+∠E=________.
【点拨】(2)如图,连接CD.
由(1)可得∠B+∠E=∠1+∠2,
∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2
=∠A+∠ACD+∠ADC=180°.
180°
第13章 三角形中的边角关系、命题与证明
13.2 命题与证明
三角形外角的性质
答案显示
不相邻;大于
延长线;2;相等
D
A
C
A
核心必知
基础巩固练
C
360°
答案显示
能力提升练
基础巩固练
B
101°
∠1>∠2>∠3
C
能力提升练
360
D
1.三角形的一边与另一边的________组成的角,叫三角形的外角;三角形的每个顶点处都有________个外角,且这两个外角________.
2.三角形的外角等于与它________的两个内角的和;因此它________与它不相邻的任一内角.
3.三角形的外角和等于________.
延长线
2
相等
不相邻
大于
360°
1.下列选项中,∠1为三角形的外角的是( )
D
2.关于三角形的外角,下列说法中错误的是( )
A.一个三角形只有三个外角
B.三角形的每个顶点处都有两个外角
C.三角形的每个外角是与它相邻内角的邻补角
D.一个三角形共有六个外角
A
3.[中考·甘孜州]如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
A.110° B.80°
C.70° D.60°
C
4.[2019·六安裕安区月考]将一副三角板按如图所示的方式叠放,则∠α等于( )
A.75° B.60°
C.45° D.30°
A
5.[2019·蚌埠淮上区期末]如图,∠1的度数为( )
A.100° B.110°
C.120° D.130°
C
6.[2018·合肥庐阳区期末]如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2=______________.
101°
7.如图,在△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连接EF,则∠1,∠2,∠3的大小关系是____________________.
∠1>∠2>∠3
8.如图,D是△ABC的边BC上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
解:∵∠BAC+∠B+∠C=180°,∠BAC=70°,
∠B=40°,∴∠C=70°.
解:∵∠ADC=∠B+∠BAD=80°,∠B=∠BAD,∴∠B=40°.
9.如图,AD平分∠BAC,∠EAD=∠EDA,那么∠EAC与∠B相等吗?为什么?
解:相等;理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∠EAD=∠EDA,
∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
10.下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
C
11.一块试验田的形状为等边三角形(设其为△ABC),为了了解情况,管理员甲从顶点A出发,沿AB→BC→CA的方向走了一圈回到顶点A处.管理员乙从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到出发点D处.则甲、乙两位管理员从出发到回到原处的途中身体( )
A.甲、乙都转过180°
B.甲、乙都转过360°
C.甲转过120°,乙转过180°
D.甲转过240°,乙转过360°
D
12.[2018·安庆期末]已知直线l1∥l2,一块含30°角的直角三角尺如图所示放置,∠1=25°,则∠2等于( )
A.30° B.35°
C.40° D.45°
B
13.[2018·合肥45中期中]如图,D,E,F分别是△ABC的边BC,AC,AB上的点,则∠1+∠2+∠3+∠4+∠5+∠6=________°.
360
【点拨】设BE和CF交于点N,则∠4=∠ECN+∠ENC.
∵∠ENC=∠FNB,∴∠4=∠ECN+∠FNB.
∵∠5+∠2+∠3+∠ECN=∠1+∠6+∠FNB=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6
=∠1+∠2+∠3+∠ECN+∠FNB+∠5+∠6
=(∠2+∠3+∠5+∠ECN)+(∠1+∠6+∠FNB)
=180°+180°=360°.
14.[2018·合肥瑶海区期末]如图,点D是△ABC的边BC上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.
解:∵∠1=∠2,∠3=∠4,∠4=∠1+∠2,
∴∠3=2∠2.∵∠BAC=66°,
∴∠2+∠3=180°-66°=114°,
即3∠2=114°.∴∠2=38°,∠3=76°.
∴∠DAC=180°-2∠3=180°-2×76°=28°.
15.[2017·阜阳颍州区月考]如图,AD平分∠EAC,交BC的延长线于点D,若∠B=40°,∠ACD=100°,求∠DAE的度数.
16.如图,在△ABC中,∠1=∠2=∠3.
(1)求证:∠BAC=∠DEF;
证明:在△ACE中,∠DEF=∠3+∠CAE,
∵∠1=∠3,∴∠DEF=∠1+∠CAE=∠BAC,
即∠BAC=∠DEF.
16.如图,在△ABC中,∠1=∠2=∠3.
(2)若∠BAC=70°,∠DFE=50°,求∠ABC的度数.
解:在△BCF中,∠DFE=∠2+∠BCF,
∵∠2=∠3,∴∠DFE=∠3+∠BCF,
即∠DFE=∠ACB.
∵∠BAC=70°,∠DFE=50°,
∴∠ABC=180°-∠BAC-∠ACB
=180°-70°-50°=60°.
17.(1)如图①,AC,BD交于点O,连接AD,BC.
求证:∠A+∠D=∠B+∠C;
证明:∵∠AOB是△AOD的外角,
∴∠A+∠D=∠AOB.
∵∠AOB是△BOC的外角,
∴∠B+∠C=∠AOB.
∴∠A+∠D=∠B+∠C.
(2)如图②,利用(1)中结论计算:∠A+∠B+∠C+∠D+∠E=________.
【点拨】(2)如图,连接CD.
由(1)可得∠B+∠E=∠1+∠2,
∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2
=∠A+∠ACD+∠ADC=180°.
180°
