沪科版八上数学第13章 三角形中的边角关系、命题与证明 章末小测课件(22张PPT)
文档属性
| 名称 | 沪科版八上数学第13章 三角形中的边角关系、命题与证明 章末小测课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 557.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 15:39:46 | ||
图片预览







文档简介
(共22张PPT)
章末小测
第13章 三角形中的边角关系、命题与证明
答案显示
A
B
C
60°
如果两个角互余,那么这两个角的和为90°
C
D
A
A
A
答案显示
60
20°
已知;EC;内错角相等,两直线平行;两直线平行,内错角相等;已知;∠4;等量代换;内错角相等,两直线平行
1.下列长度的各组线段中,能组成三角形的是( )
A.1,1,2
B.3,7,11
C.6,8,9
D.3,3,6
C
2.下列语句中,不是命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.不是对顶角,不相等
D.过直线AB外一点P作直线AB的垂线
D
3.已知a,b,c为三角形三边的长,化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|的结果是( )
A.0 B.2a+2b+2c
C.4a D.2b-2c
A
4.若△ABC的三个内角满足关系式∠B+∠C=3∠A,则这个三角形( )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
A
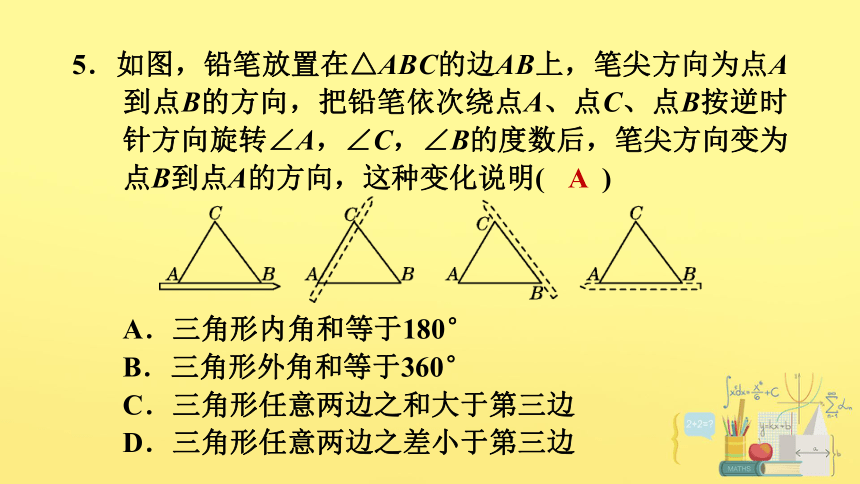
5.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A,∠C,∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明( )
A.三角形内角和等于180°
B.三角形外角和等于360°
C.三角形任意两边之和大于第三边
D.三角形任意两边之差小于第三边
A
6.当三角形中一个内角α是另一个内角β的2倍时,我们称此三角形为“标准三角形”,α为“标准角”,如果一个“标准三角形”的“标准角”为100°,那么这个“标准三角形”的最小内角度数为( )
A.30° B.45° C.50° D.60°
A
7.如图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2等于( )
A.52° B.61°
C.65° D.70°
B
8.如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.40° B.70°
C.80° D.100°
C
60°
10.写出“如果两个角的和为90°,那么这两个角互余”的逆命题:________________________________________.
如果两个角互余,那么这两个角的和为90°
11.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC=________.
20°
12.如图,点D在△ABC的边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE=________°.
60
13.完成以下证明,并在括号内填写理由:
已知:如图,∠1=∠2,∠A=∠3.求证:AC∥DE.
证明:因为∠1=∠2( ),
所以AB∥________( ).
所以∠A=∠4( ).
又因为∠A=∠3( ),
所以∠3=________( ).
所以AC∥DE( ).
已知
EC
内错角相等,两直线平行
两直线平行,内错角相等
已知
∠4
等量代换
内错角相等,两直线平行
14.两只猎豹在A处发现有一只野牛离开群体所在的D处独自去O处觅食,猎豹打算用迂回的方式,由一只先从A处前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,猎豹从C处要转多少度才能直达B处?
解:因为∠BAC=40°,∠ABC=70°,
所以∠LCB=∠BAC+∠ABC
=40°+70°=110°.
所以猎豹从C处要转110°才能直达B处.
15.如图,在△ABC中,AB=AC,BD是角平分线,BD=AD,求∠A的度数.
解:设∠A=x°,∵BD=AD,
∴△ABD是等腰三角形,
∴∠ABD=∠A=x°.
∵BD是角平分线,∴∠ABC=2x°.
∵AB=AC,∴△ABC是等腰三角形,
∴∠C=∠ABC=2x°.
易知x+2x+2x=180, 解得x=36,∴∠A=36°.
16.已知一个等腰三角形的三边长分别为x,2x-1,5x-3,求这个等腰三角形的周长.
解:①若x=2x-1,解得x=1,则三边长分别为1,1,2,不能组成三角形;
综上可知,这个等腰三角形的周长为2.
17.[2018·宜昌]如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
17.[2018·宜昌]如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
解:∵∠ACB=90°,∠CBE=65°,
∴∠CEB=∠ACB-∠CBE=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
章末小测
第13章 三角形中的边角关系、命题与证明
答案显示
A
B
C
60°
如果两个角互余,那么这两个角的和为90°
C
D
A
A
A
答案显示
60
20°
已知;EC;内错角相等,两直线平行;两直线平行,内错角相等;已知;∠4;等量代换;内错角相等,两直线平行
1.下列长度的各组线段中,能组成三角形的是( )
A.1,1,2
B.3,7,11
C.6,8,9
D.3,3,6
C
2.下列语句中,不是命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.不是对顶角,不相等
D.过直线AB外一点P作直线AB的垂线
D
3.已知a,b,c为三角形三边的长,化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|的结果是( )
A.0 B.2a+2b+2c
C.4a D.2b-2c
A
4.若△ABC的三个内角满足关系式∠B+∠C=3∠A,则这个三角形( )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
A
5.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A,∠C,∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明( )
A.三角形内角和等于180°
B.三角形外角和等于360°
C.三角形任意两边之和大于第三边
D.三角形任意两边之差小于第三边
A
6.当三角形中一个内角α是另一个内角β的2倍时,我们称此三角形为“标准三角形”,α为“标准角”,如果一个“标准三角形”的“标准角”为100°,那么这个“标准三角形”的最小内角度数为( )
A.30° B.45° C.50° D.60°
A
7.如图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2等于( )
A.52° B.61°
C.65° D.70°
B
8.如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.40° B.70°
C.80° D.100°
C
60°
10.写出“如果两个角的和为90°,那么这两个角互余”的逆命题:________________________________________.
如果两个角互余,那么这两个角的和为90°
11.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC=________.
20°
12.如图,点D在△ABC的边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE=________°.
60
13.完成以下证明,并在括号内填写理由:
已知:如图,∠1=∠2,∠A=∠3.求证:AC∥DE.
证明:因为∠1=∠2( ),
所以AB∥________( ).
所以∠A=∠4( ).
又因为∠A=∠3( ),
所以∠3=________( ).
所以AC∥DE( ).
已知
EC
内错角相等,两直线平行
两直线平行,内错角相等
已知
∠4
等量代换
内错角相等,两直线平行
14.两只猎豹在A处发现有一只野牛离开群体所在的D处独自去O处觅食,猎豹打算用迂回的方式,由一只先从A处前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,猎豹从C处要转多少度才能直达B处?
解:因为∠BAC=40°,∠ABC=70°,
所以∠LCB=∠BAC+∠ABC
=40°+70°=110°.
所以猎豹从C处要转110°才能直达B处.
15.如图,在△ABC中,AB=AC,BD是角平分线,BD=AD,求∠A的度数.
解:设∠A=x°,∵BD=AD,
∴△ABD是等腰三角形,
∴∠ABD=∠A=x°.
∵BD是角平分线,∴∠ABC=2x°.
∵AB=AC,∴△ABC是等腰三角形,
∴∠C=∠ABC=2x°.
易知x+2x+2x=180, 解得x=36,∴∠A=36°.
16.已知一个等腰三角形的三边长分别为x,2x-1,5x-3,求这个等腰三角形的周长.
解:①若x=2x-1,解得x=1,则三边长分别为1,1,2,不能组成三角形;
综上可知,这个等腰三角形的周长为2.
17.[2018·宜昌]如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
17.[2018·宜昌]如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
解:∵∠ACB=90°,∠CBE=65°,
∴∠CEB=∠ACB-∠CBE=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
