沪科版八上数学第13章三角形中的边角关系、命题与证明达标测试卷(含答案)
文档属性
| 名称 | 沪科版八上数学第13章三角形中的边角关系、命题与证明达标测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 136.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览



文档简介
第13章达标测试卷
一、选择题(每题3分,共30分)
1.在一个直角三角形中,有一个锐角等于40°,则另一个锐角的度数是( )
A.40° B.50° C.60° D.70°
2.下列每组数分别表示三根木棒的长,将木棒首尾连接后,能摆成三角形的一组是( )
A.1,2,1 B.1,2,2 C.1,2,3 D.1,2,4
3.等腰三角形的两边长分别为6和3,则这个三角形的周长是( )
A.12 B.15 C.12或15 D.18
4.下面给出的四个命题中,假命题是( )
A.如果a=3,那么|a|=3
B.如果x2=4,那么x=±2
C.如果(a-1)(a+2)=0,那么a-1=0或a+2=0
D.如果(a-1)2+(b+2)2=0,那么a=1或b=-2
5.对于命题“如果∠1+∠2=180°,那么∠1≠∠2”,能说明它是假命题的例子是( )
A.∠1=100°,∠2=80° B.∠1=50°,∠2=50°
C.∠1=∠2=90° D.∠1=80°,∠2=80°
6.若a,b,c是△ABC的三边长,且a2+b2-6a-10b+34=0,则c的取值范围是( )
A.c<8 B.2<c<8 C.2≤c≤8 D.4<c<16
7.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118° B.119°
C.120° D.121°
8.如图,AD是∠CAE的平分线,∠B=35°,∠DAC=60°,则∠ACD等于( )
A.25°
B.85°
C.60°
D.95°
9.如图,点D,E在△ABC的边上,CD与BE相交于点F,则∠1,∠2,∠3,∠4应满足的关系是( )
A.∠1+∠4=∠2+∠3
B.∠1+∠2=∠3+∠4
C.∠1+∠2=∠4-∠3
D.∠2-∠1=∠3+∠4
10.小明把一副含45°,30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.360°
C.210° D.270°
二、填空题(每题3分,共18分)
11.命题“和为180°的两个角互为补角”的逆命题是_____________________________________________________________.
12.如图,直线m∥n,直角三角形ABC的顶点A在直线n上,∠C=90°.若∠1=25°,∠2=70°,则∠B=________.
13.如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线.若∠B=71°,则∠BAC=________.
14.如图,在△ABC中,点P是△ABC的角平分线的交点,则∠PBC+∠PCA+∠PAB=________度.
15.如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,则∠ACD的度数为________.
16.在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α,∠B增加β,∠C增加γ,则α、β、γ三者之间的数量关系是__________.
三、解答题(17,18题每题8分,其余每题9分,共52分)
17.如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1=________________,∠2=________________;
(2)请观察∠1、∠2分别与∠ABC有怎样的关系,归纳出一个命题.
INCLUDEPICTURE"17-16.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\17-16.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\17-16.tif" \* MERGEFORMATINET
18.梦雪的爸爸将一段长为30米的破旧渔网围成一个三角形,已知第一条边长为a米,第二条边长比第一条边长的2倍还多2米.
(1)请用a表示第三条边长;
(2)请求出a的取值范围.
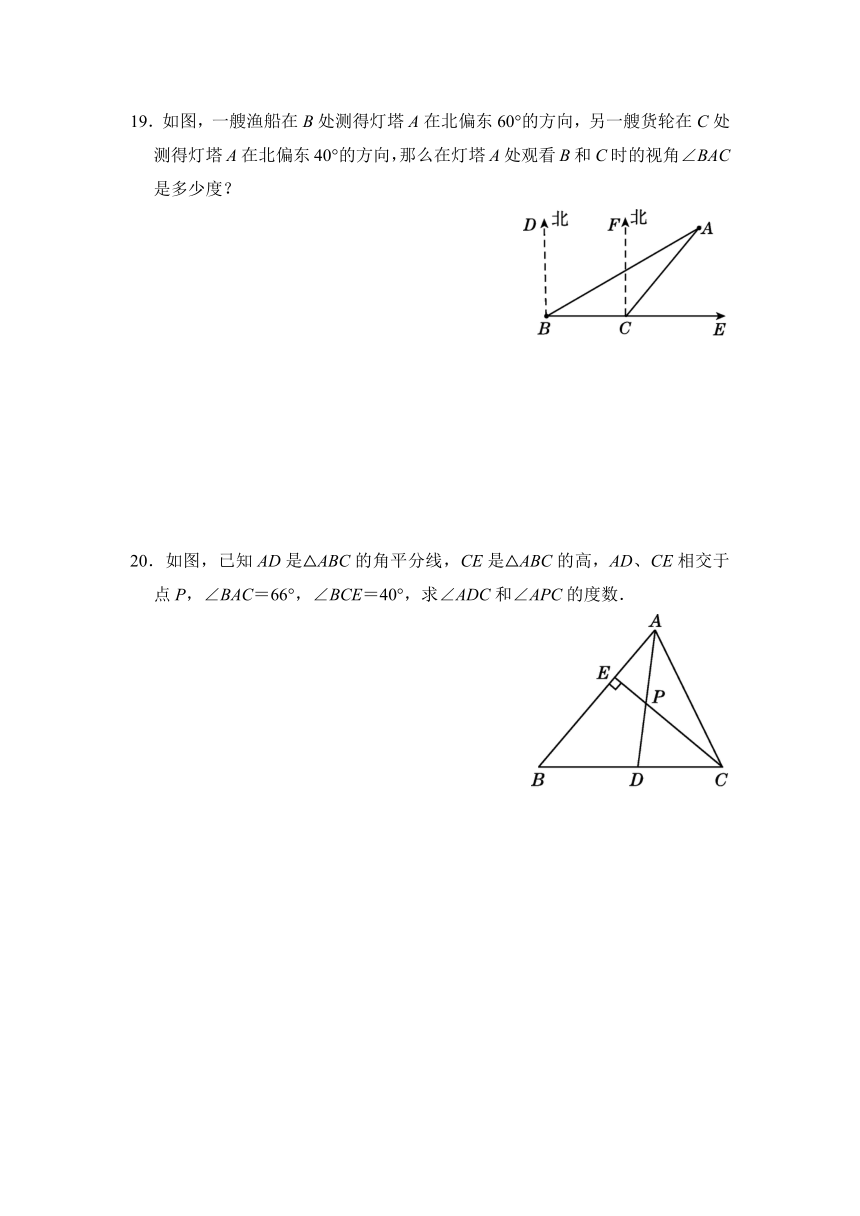
19.如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?
INCLUDEPICTURE"U171.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\U171.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\U171.tif" \* MERGEFORMATINET
20.如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD、CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
INCLUDEPICTURE"R26.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\R26.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\R26.tif" \* MERGEFORMATINET
21.如图①,AD,AE分别是△ABC中BC边上的高和中线,已知AD=5 cm,EC=3.5 cm.
(1)求△ABE和△AEC的面积;
(2)通过做题,你能发现什么结论?
(3)根据(2)中的结论,解决下列问题:如图②,CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线.若△AEF的面积为1 cm2,求△ABC的面积.
INCLUDEPICTURE"PPJ22.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\PPJ22.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\PPJ22.tif" \* MERGEFORMATINET
22.如图①,在△ABC中,AE平分∠BAC,∠C>∠B,F是AE上一点,且FD⊥BC于D点.
(1)试猜想∠EFD,∠B,∠C的关系,并说明理由;
(2)如图②,当点F在AE的延长线上时,其余条件不变,(1)中的结论还成立吗?说明理由.
INCLUDEPICTURE"TT19.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\TT19.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\TT19.tif" \* MERGEFORMATINET
②
答案
一、1.B
2.B 点拨:根据三角形的三边关系:三角形中任何两边的和大于第三边,计算两较小边的和,看看是否大于第三边即可.只有B选项中1+2>2,能组成三角形,故选B.
3.B 4.D
5.C 点拨:A满足条件∠1+∠2=180°,也满足结论∠1≠∠2,故错误; B不满足条件,也不满足结论,故错误; C满足条件,不满足结论,故正确; D不满足条件,也不满足结论,故错误.
6.B 7.C
8.D 点拨:由题意得∠CAD=∠DAE=60°,∴∠BAC=60°,∴∠ACD=∠B+∠BAC=35°+60°=95°.
9.D 10.C
二、11.互为补角的两个角的和为180°
12.45° 点拨:∵m∥n,∴∠2=∠BAC+∠1.∴∠BAC=∠2-∠1=45°,∴∠B=90°-∠BAC=45°.
13.38° 点拨:∵AD∥BC,∴∠EAD=∠B=71°.∵AD是∠EAC的平分线,∴∠EAC=2∠EAD=142°,∴∠BAC=38°.
14.90
15.83° 点拨:∵DF⊥AB,∴∠AFE=90°.
∴∠AEF=90°-∠A=90°-35°=55°.∴∠CED=∠AEF=55°.∴∠ACD=180°-∠CED-∠D=180°-55°-42°=83°.
16.α=β+γ 点拨:∵三角形内角和是一个定值,为180°,∴∠A+∠B+∠C=180°.当∠A越来越小,∠B、∠C越来越大时,∠A-α+∠B+β+∠C+γ=180°,∴α=β+γ.
三、17.解:(1)25°;155°
(2)∠1=∠ABC,∠2+∠ABC=180°.命题:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
18.解:(1)第三条边长为30-a-(2a+2)=28-3a(米).
(2)根据三角形三边关系,得2a+2-a<28-3a<2a+2+a,解得<a<.
19.解:依题意,得∠DBA=60°,∠FCA=40°.
∴∠ABC=∠DBC-∠DBA=90°-60°=30°,∠BCA=∠BCF+∠FCA=90°+40°=130°.
∴ 在△ABC中, ∠BAC=180°-∠ABC-∠BCA=180°-30°-130°=20°.
答:在灯塔A处观看B和C时的视角∠BAC是20°.
20.解:∵CE⊥AB,∴∠AEC=90°.
∴∠ACE=180°-∠BAC-∠AEC=24°.
∵AD平分∠BAC,∴∠DAC=∠BAC=33°.
∵∠BCE=40°,∴∠ACB=40°+24°=64°.
∴∠ADC=180°-∠DAC-∠ACB=83°.
∴∠APC=∠ADC+∠BCE=83°+40°=123°.
21.解:(1)∵AE是△ABC中BC边上的中线,
∴BE=EC=3.5 cm.
∴S△ABE=·BE·AD=×3.5×5=(cm2),S△AEC=·EC·AD=×3.5×5=(cm2).
(2)三角形的中线将三角形分成两个面积相等的三角形.
(3)由(2)中的结论,可得S△ABC=2S△ACD=4S△ADE=8S△AEF=8×1=8(cm2).
22.解:(1)∠EFD=∠C-∠B.
理由如下:由AE是∠BAC的平分线知∠BAE=∠BAC.
由三角形外角的性质知∠FED=∠B+∠BAC,
故∠B+∠BAC+∠EFD=90°①.
由三角形内角和定理,得∠B+∠BAC+∠C=180°,
所以∠C+∠B+∠BAC=90°②.
②-①,得∠EFD=∠C-∠B.
(2)成立.理由如下:
由对顶角相等和三角形的外角性质知∠FED=∠AEC=∠B+∠BAC,故∠B+∠BAC+∠EFD=90°③.
由三角形内角和定理,得∠B+∠BAC+∠C=180°,
所以∠B+∠BAC+∠C=90°④.
④-③,得∠EFD=∠C-∠B.
一、选择题(每题3分,共30分)
1.在一个直角三角形中,有一个锐角等于40°,则另一个锐角的度数是( )
A.40° B.50° C.60° D.70°
2.下列每组数分别表示三根木棒的长,将木棒首尾连接后,能摆成三角形的一组是( )
A.1,2,1 B.1,2,2 C.1,2,3 D.1,2,4
3.等腰三角形的两边长分别为6和3,则这个三角形的周长是( )
A.12 B.15 C.12或15 D.18
4.下面给出的四个命题中,假命题是( )
A.如果a=3,那么|a|=3
B.如果x2=4,那么x=±2
C.如果(a-1)(a+2)=0,那么a-1=0或a+2=0
D.如果(a-1)2+(b+2)2=0,那么a=1或b=-2
5.对于命题“如果∠1+∠2=180°,那么∠1≠∠2”,能说明它是假命题的例子是( )
A.∠1=100°,∠2=80° B.∠1=50°,∠2=50°
C.∠1=∠2=90° D.∠1=80°,∠2=80°
6.若a,b,c是△ABC的三边长,且a2+b2-6a-10b+34=0,则c的取值范围是( )
A.c<8 B.2<c<8 C.2≤c≤8 D.4<c<16
7.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118° B.119°
C.120° D.121°
8.如图,AD是∠CAE的平分线,∠B=35°,∠DAC=60°,则∠ACD等于( )
A.25°
B.85°
C.60°
D.95°
9.如图,点D,E在△ABC的边上,CD与BE相交于点F,则∠1,∠2,∠3,∠4应满足的关系是( )
A.∠1+∠4=∠2+∠3
B.∠1+∠2=∠3+∠4
C.∠1+∠2=∠4-∠3
D.∠2-∠1=∠3+∠4
10.小明把一副含45°,30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.360°
C.210° D.270°
二、填空题(每题3分,共18分)
11.命题“和为180°的两个角互为补角”的逆命题是_____________________________________________________________.
12.如图,直线m∥n,直角三角形ABC的顶点A在直线n上,∠C=90°.若∠1=25°,∠2=70°,则∠B=________.
13.如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线.若∠B=71°,则∠BAC=________.
14.如图,在△ABC中,点P是△ABC的角平分线的交点,则∠PBC+∠PCA+∠PAB=________度.
15.如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,则∠ACD的度数为________.
16.在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α,∠B增加β,∠C增加γ,则α、β、γ三者之间的数量关系是__________.
三、解答题(17,18题每题8分,其余每题9分,共52分)
17.如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1=________________,∠2=________________;
(2)请观察∠1、∠2分别与∠ABC有怎样的关系,归纳出一个命题.
INCLUDEPICTURE"17-16.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\17-16.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\17-16.tif" \* MERGEFORMATINET
18.梦雪的爸爸将一段长为30米的破旧渔网围成一个三角形,已知第一条边长为a米,第二条边长比第一条边长的2倍还多2米.
(1)请用a表示第三条边长;
(2)请求出a的取值范围.
19.如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?
INCLUDEPICTURE"U171.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\U171.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\U171.tif" \* MERGEFORMATINET
20.如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD、CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
INCLUDEPICTURE"R26.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\R26.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\R26.tif" \* MERGEFORMATINET
21.如图①,AD,AE分别是△ABC中BC边上的高和中线,已知AD=5 cm,EC=3.5 cm.
(1)求△ABE和△AEC的面积;
(2)通过做题,你能发现什么结论?
(3)根据(2)中的结论,解决下列问题:如图②,CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线.若△AEF的面积为1 cm2,求△ABC的面积.
INCLUDEPICTURE"PPJ22.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\PPJ22.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\PPJ22.tif" \* MERGEFORMATINET
22.如图①,在△ABC中,AE平分∠BAC,∠C>∠B,F是AE上一点,且FD⊥BC于D点.
(1)试猜想∠EFD,∠B,∠C的关系,并说明理由;
(2)如图②,当点F在AE的延长线上时,其余条件不变,(1)中的结论还成立吗?说明理由.
INCLUDEPICTURE"TT19.tif" INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\TT19.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\19秋初中\\数学\\8HK 点训\\word\\TT19.tif" \* MERGEFORMATINET
②
答案
一、1.B
2.B 点拨:根据三角形的三边关系:三角形中任何两边的和大于第三边,计算两较小边的和,看看是否大于第三边即可.只有B选项中1+2>2,能组成三角形,故选B.
3.B 4.D
5.C 点拨:A满足条件∠1+∠2=180°,也满足结论∠1≠∠2,故错误; B不满足条件,也不满足结论,故错误; C满足条件,不满足结论,故正确; D不满足条件,也不满足结论,故错误.
6.B 7.C
8.D 点拨:由题意得∠CAD=∠DAE=60°,∴∠BAC=60°,∴∠ACD=∠B+∠BAC=35°+60°=95°.
9.D 10.C
二、11.互为补角的两个角的和为180°
12.45° 点拨:∵m∥n,∴∠2=∠BAC+∠1.∴∠BAC=∠2-∠1=45°,∴∠B=90°-∠BAC=45°.
13.38° 点拨:∵AD∥BC,∴∠EAD=∠B=71°.∵AD是∠EAC的平分线,∴∠EAC=2∠EAD=142°,∴∠BAC=38°.
14.90
15.83° 点拨:∵DF⊥AB,∴∠AFE=90°.
∴∠AEF=90°-∠A=90°-35°=55°.∴∠CED=∠AEF=55°.∴∠ACD=180°-∠CED-∠D=180°-55°-42°=83°.
16.α=β+γ 点拨:∵三角形内角和是一个定值,为180°,∴∠A+∠B+∠C=180°.当∠A越来越小,∠B、∠C越来越大时,∠A-α+∠B+β+∠C+γ=180°,∴α=β+γ.
三、17.解:(1)25°;155°
(2)∠1=∠ABC,∠2+∠ABC=180°.命题:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
18.解:(1)第三条边长为30-a-(2a+2)=28-3a(米).
(2)根据三角形三边关系,得2a+2-a<28-3a<2a+2+a,解得<a<.
19.解:依题意,得∠DBA=60°,∠FCA=40°.
∴∠ABC=∠DBC-∠DBA=90°-60°=30°,∠BCA=∠BCF+∠FCA=90°+40°=130°.
∴ 在△ABC中, ∠BAC=180°-∠ABC-∠BCA=180°-30°-130°=20°.
答:在灯塔A处观看B和C时的视角∠BAC是20°.
20.解:∵CE⊥AB,∴∠AEC=90°.
∴∠ACE=180°-∠BAC-∠AEC=24°.
∵AD平分∠BAC,∴∠DAC=∠BAC=33°.
∵∠BCE=40°,∴∠ACB=40°+24°=64°.
∴∠ADC=180°-∠DAC-∠ACB=83°.
∴∠APC=∠ADC+∠BCE=83°+40°=123°.
21.解:(1)∵AE是△ABC中BC边上的中线,
∴BE=EC=3.5 cm.
∴S△ABE=·BE·AD=×3.5×5=(cm2),S△AEC=·EC·AD=×3.5×5=(cm2).
(2)三角形的中线将三角形分成两个面积相等的三角形.
(3)由(2)中的结论,可得S△ABC=2S△ACD=4S△ADE=8S△AEF=8×1=8(cm2).
22.解:(1)∠EFD=∠C-∠B.
理由如下:由AE是∠BAC的平分线知∠BAE=∠BAC.
由三角形外角的性质知∠FED=∠B+∠BAC,
故∠B+∠BAC+∠EFD=90°①.
由三角形内角和定理,得∠B+∠BAC+∠C=180°,
所以∠C+∠B+∠BAC=90°②.
②-①,得∠EFD=∠C-∠B.
(2)成立.理由如下:
由对顶角相等和三角形的外角性质知∠FED=∠AEC=∠B+∠BAC,故∠B+∠BAC+∠EFD=90°③.
由三角形内角和定理,得∠B+∠BAC+∠C=180°,
所以∠B+∠BAC+∠C=90°④.
④-③,得∠EFD=∠C-∠B.
