沪科版八上数学12.2一次函数与一元一次方程、不等式习题课件(32张)
文档属性
| 名称 | 沪科版八上数学12.2一次函数与一元一次方程、不等式习题课件(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
第12章 一次函数
12.2 一次函数
一次函数与一元一次方程、不等式
答案显示
y=kx+b;
上方;下方
kx+b;x轴;横;x轴;横
C
(5,0);x=5
x=2
(1)x=2. (2)-1.
(3)x=-1.
核心必知
基础巩固练
答案显示
A
C
≥2
x>-2
图略。
(1)x=-0.5.
(2)x≥-0.5.
(3)-2≤x≤1.
-1<x<2
答案显示
②③④
(1)x取2. (2)x>2. (3)x<2.
能力提升练
(1)y1=80+15x(x≥0),y2=30x(x≥0). 图略.
答案显示
素养核心练
横、纵坐标都是整数的点有(2,-20),
(5,-15),(8,-10),(11,-5),
(14,0),共5个.
1.一元一次方程kx+b=0(k≠0,k,b为常数)的解即为函数y=________的图象与________的交点的______坐标;反之,函数y=kx+b(k≠0,k,b为常数)的图象与________的交点的______坐标即为方程kx+b=0的解.
kx+b
x轴
横
x轴
横
2.一元一次不等式kx+b>0(或kx+b<0)的解集,就是一次函数______________的图象在x轴________(或________)相应的自变量x的取值范围.
y=kx+b
上方
下方
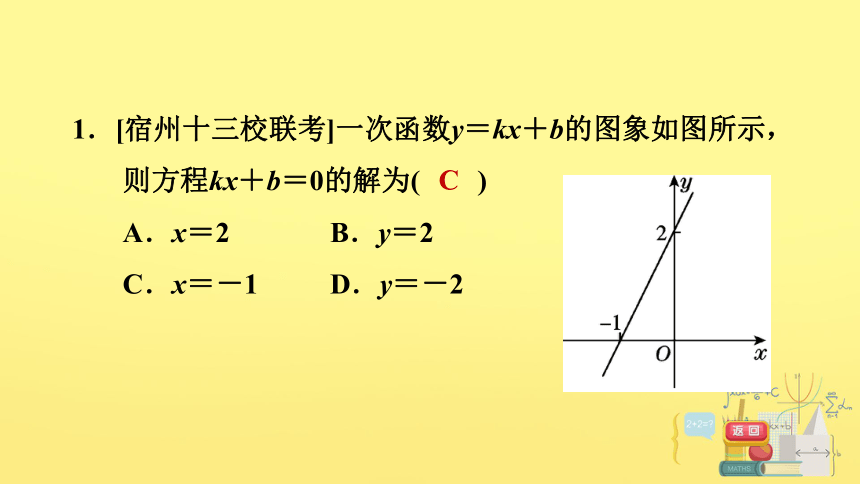
1.[宿州十三校联考]一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2 B.y=2
C.x=-1 D.y=-2
C
2.直线y=-2x+10与x轴的交点坐标是________,则方程-2x+10=0的解是________.
(5,0)
x=5
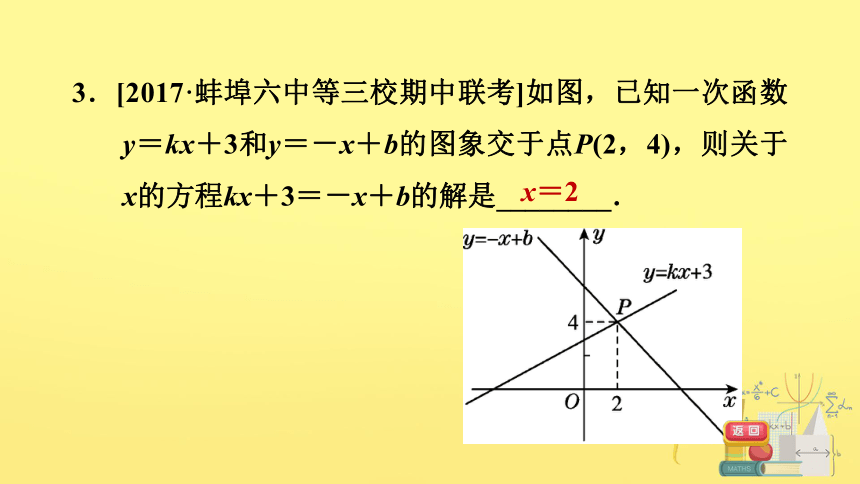
3.[2017·蚌埠六中等三校期中联考]如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的方程kx+3=-x+b的解是________.
x=2
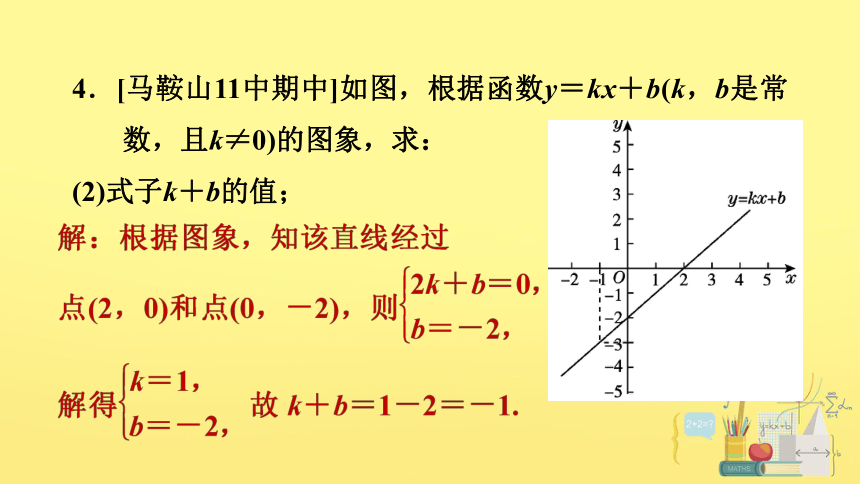
4.[马鞍山11中期中]如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
解:当y=0时,x=2.
故方程kx+b=0的解是x=2.
4.[马鞍山11中期中]如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(2)式子k+b的值;
4.[马鞍山11中期中]如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(3)方程kx+b=-3的解.
解:当y=-3时,x=-1.
故方程kx+b=-3的解是x=-1.
【答案】C
6.[中考·百色]直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A.x≤3 B.x≥3
C.x≥-3 D.x≤0
A
7.[中考·永州]已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x_______时,y≤0.
【点拨】由一次函数y=kx+b的图象过A(0,1),B(2,0)知y随x的增大而减小.
≥2
8.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为__________________.
【点拨】此题运用数形结合思想,观察题图知不等式-2<kx+b<1的解集就是线段AB(不包含端点)所对应的自变量x的取值范围.
-1<x<2
9.直线l1:y=k1x,l2:y=k2x+b在同一坐标系中的图象如图所示,则关于x的不等式k1x<k2x+b的解集是________.
x>-2
10.[2018·阜阳颍上五中期中]在如图所示的平面直角坐标系中画出函数y=2x+1的图象,利用图象:
(1)求方程2x+1=0的解;
解:如图.
由图象知,方程2x+1=0的解是x=-0.5.
(2)求不等式2x+1≥0的解集;
(3)若-3≤y≤3,求x的取值范围.
由图象知,当-3≤y≤3时,x的取值范围是-2≤x≤1.
解:由图象知,不等式2x+1≥0的解集是x≥-0.5.
11.[安庆期末]函数y=kx+b的图象如图所示,下列结论:①k>0;②b>0;③k+b>0;④2k+b=0;⑤不等式kx+b<0的解集是x<2,其中正确的是________.(填序号)
【点拨】由函数图象可知k<0,b>0;当x=1时,y=k+b>0;当x=2时,y=2k+b=0;由函数图象可得不等式kx+b<0的解集是x>2.故②③④正确.
②③④
12.已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(1)一次函数的表达式为_____________;
(2)关于x的方程kx+b=0的解为________;
x=8
12.已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(3)求该函数图象与两坐标轴围成的三角形的面积.
13.如图,对照图象,请回答下列问题:
(1)当x取何值时,2x-5=-x+1?
解:由图象可知,直线y=2x-5与直线y=-x+1的交点的横坐标是2,所以当x取2时,2x-5=-x+1.
13.如图,对照图象,请回答下列问题:
(2)当x取何值时,2x-5>-x+1?
(3)当x取何值时,2x-5<-x+1?
解:由图象可知,当x>2时,直线y=2x-5在直线y=-x+1的上方,即2x-5>-x+1.
由图象可知,当x<2时,直线y=2x-5在直线y=-x+1的下方,即2x-5<-x+1.
14.五一期间,小明一家乘坐高铁前往某市旅游,到达后计划租用新能源汽车自驾出游.有甲、乙两家公司提供新能源汽车出租服务.甲公司:每日收取固定租金80元,另外收取每小时15元的租金.乙公司:无固定租金,直接以租车时间计费,每小时租金30元.
设租车时间为x小时,甲、乙两家公司
的租车费用分别为y1元,y2元.
(1)分别写出y1,y2与x之间的函数表达式,
并在如图所示的坐标系中作出这两个
函数的图象;
解:y1=80+15x(x≥0),y2=30x(x≥0).
两个函数的图象如图所示.
14.五一期间,小明一家乘坐高铁前往某市旅游,到达后计划租用新能源汽车自驾出游.有甲、乙两家公司提供新能源汽车出租服务.甲公司:每日收取固定租金80元,另外收取每小时15元的租金.乙公司:无固定租金,直接以租车时间计费,每小时租金30元.设租车时间为x小时,甲、乙两家公司的租车费用分别为y1元,y2元.
(2)选择哪家公司租车更省钱?
第12章 一次函数
12.2 一次函数
一次函数与一元一次方程、不等式
答案显示
y=kx+b;
上方;下方
kx+b;x轴;横;x轴;横
C
(5,0);x=5
x=2
(1)x=2. (2)-1.
(3)x=-1.
核心必知
基础巩固练
答案显示
A
C
≥2
x>-2
图略。
(1)x=-0.5.
(2)x≥-0.5.
(3)-2≤x≤1.
-1<x<2
答案显示
②③④
(1)x取2. (2)x>2. (3)x<2.
能力提升练
(1)y1=80+15x(x≥0),y2=30x(x≥0). 图略.
答案显示
素养核心练
横、纵坐标都是整数的点有(2,-20),
(5,-15),(8,-10),(11,-5),
(14,0),共5个.
1.一元一次方程kx+b=0(k≠0,k,b为常数)的解即为函数y=________的图象与________的交点的______坐标;反之,函数y=kx+b(k≠0,k,b为常数)的图象与________的交点的______坐标即为方程kx+b=0的解.
kx+b
x轴
横
x轴
横
2.一元一次不等式kx+b>0(或kx+b<0)的解集,就是一次函数______________的图象在x轴________(或________)相应的自变量x的取值范围.
y=kx+b
上方
下方
1.[宿州十三校联考]一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2 B.y=2
C.x=-1 D.y=-2
C
2.直线y=-2x+10与x轴的交点坐标是________,则方程-2x+10=0的解是________.
(5,0)
x=5
3.[2017·蚌埠六中等三校期中联考]如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的方程kx+3=-x+b的解是________.
x=2
4.[马鞍山11中期中]如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
解:当y=0时,x=2.
故方程kx+b=0的解是x=2.
4.[马鞍山11中期中]如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(2)式子k+b的值;
4.[马鞍山11中期中]如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(3)方程kx+b=-3的解.
解:当y=-3时,x=-1.
故方程kx+b=-3的解是x=-1.
【答案】C
6.[中考·百色]直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A.x≤3 B.x≥3
C.x≥-3 D.x≤0
A
7.[中考·永州]已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x_______时,y≤0.
【点拨】由一次函数y=kx+b的图象过A(0,1),B(2,0)知y随x的增大而减小.
≥2
8.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的解集为__________________.
【点拨】此题运用数形结合思想,观察题图知不等式-2<kx+b<1的解集就是线段AB(不包含端点)所对应的自变量x的取值范围.
-1<x<2
9.直线l1:y=k1x,l2:y=k2x+b在同一坐标系中的图象如图所示,则关于x的不等式k1x<k2x+b的解集是________.
x>-2
10.[2018·阜阳颍上五中期中]在如图所示的平面直角坐标系中画出函数y=2x+1的图象,利用图象:
(1)求方程2x+1=0的解;
解:如图.
由图象知,方程2x+1=0的解是x=-0.5.
(2)求不等式2x+1≥0的解集;
(3)若-3≤y≤3,求x的取值范围.
由图象知,当-3≤y≤3时,x的取值范围是-2≤x≤1.
解:由图象知,不等式2x+1≥0的解集是x≥-0.5.
11.[安庆期末]函数y=kx+b的图象如图所示,下列结论:①k>0;②b>0;③k+b>0;④2k+b=0;⑤不等式kx+b<0的解集是x<2,其中正确的是________.(填序号)
【点拨】由函数图象可知k<0,b>0;当x=1时,y=k+b>0;当x=2时,y=2k+b=0;由函数图象可得不等式kx+b<0的解集是x>2.故②③④正确.
②③④
12.已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(1)一次函数的表达式为_____________;
(2)关于x的方程kx+b=0的解为________;
x=8
12.已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(3)求该函数图象与两坐标轴围成的三角形的面积.
13.如图,对照图象,请回答下列问题:
(1)当x取何值时,2x-5=-x+1?
解:由图象可知,直线y=2x-5与直线y=-x+1的交点的横坐标是2,所以当x取2时,2x-5=-x+1.
13.如图,对照图象,请回答下列问题:
(2)当x取何值时,2x-5>-x+1?
(3)当x取何值时,2x-5<-x+1?
解:由图象可知,当x>2时,直线y=2x-5在直线y=-x+1的上方,即2x-5>-x+1.
由图象可知,当x<2时,直线y=2x-5在直线y=-x+1的下方,即2x-5<-x+1.
14.五一期间,小明一家乘坐高铁前往某市旅游,到达后计划租用新能源汽车自驾出游.有甲、乙两家公司提供新能源汽车出租服务.甲公司:每日收取固定租金80元,另外收取每小时15元的租金.乙公司:无固定租金,直接以租车时间计费,每小时租金30元.
设租车时间为x小时,甲、乙两家公司
的租车费用分别为y1元,y2元.
(1)分别写出y1,y2与x之间的函数表达式,
并在如图所示的坐标系中作出这两个
函数的图象;
解:y1=80+15x(x≥0),y2=30x(x≥0).
两个函数的图象如图所示.
14.五一期间,小明一家乘坐高铁前往某市旅游,到达后计划租用新能源汽车自驾出游.有甲、乙两家公司提供新能源汽车出租服务.甲公司:每日收取固定租金80元,另外收取每小时15元的租金.乙公司:无固定租金,直接以租车时间计费,每小时租金30元.设租车时间为x小时,甲、乙两家公司的租车费用分别为y1元,y2元.
(2)选择哪家公司租车更省钱?
