沪科版八上数学第12章一次函数章末小测课件(38张)
文档属性
| 名称 | 沪科版八上数学第12章一次函数章末小测课件(38张) |  | |
| 格式 | zip | ||
| 文件大小 | 753.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 10:09:56 | ||
图片预览










文档简介
(共38张PPT)
章末小测
第12章 一次函数
答案显示
C
D
B
(0,6)
m>n
C
C
A
B
C
答案显示
(-21 009,-21 010);((-2)n,(-1)n2n+1)(n为自然数).
y=x或y=-x.
(1)y=2x+4. (2)图略.4. (3)x≤-0.5.
(1)(15,900). (2)S=-180t+3 600.
(3)小东能在毕业汇演开始前到达学校.
(1)y=3x-9. (2)y=3×1-9=-6. (3)x=2.
答案显示
(1)k=-1. (2)[-2, 4]或[-2,-4].
1.某品牌迷你豆浆机成本为70元,经销商对其销量、定价进行了统计,整理如下表,下列说法正确的是( )
C
A.定价是常量,销量是变量
B.定价是变量,销量是常量
C.定价与销量都是变量,定价是自变量,销量是因变量
D.定价与销量都是变量,销量是自变量,定价是因变量
定价/元 100 110 120 130 140 150
销量/个 80 100 110 100 80 60
C
3.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.0<k≤3
C.0≤k<3 D.0<k<3
A
4.已知一次函数y1=k1x+3和y2=k2x+2.若k1>0且k2<0,则这两个一次函数图象的交点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
5.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为( )
A.y=-x-2 B.y=-x-6
C.y=-x+10 D.y=-x-1
C
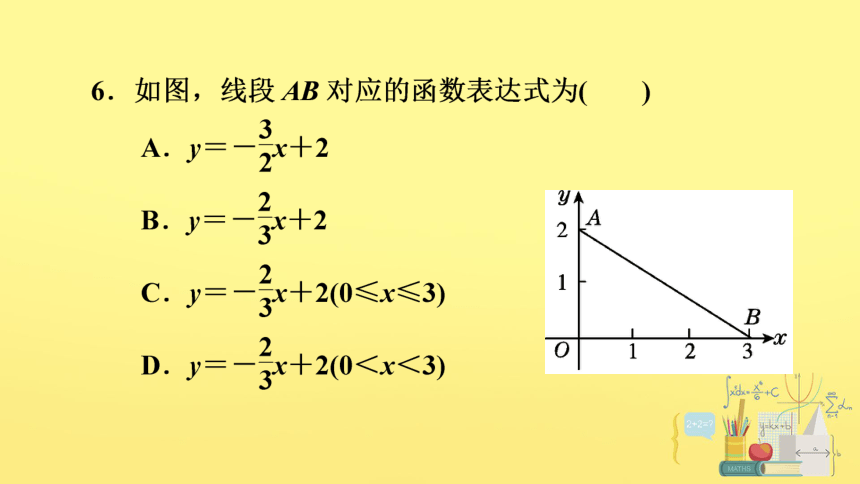
【答案】C
7.小亮家与姥姥家相距24 km,小亮8时从家出发,骑自行车去姥姥家,妈妈半小时后从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(h)的函数图象如图所示,下列结论错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5小时到达姥姥家
C.9时妈妈追上小亮
D.妈妈在距家13 km处追上小亮
【点拨】A.根据函数图象小亮去姥姥家所用时间为10-8=2(h),
所以小亮骑自行车的平均速度为24÷2=12(km/h),故正确;
B.由图象可得,妈妈到姥姥家对应的时间t=9.5,小亮到姥姥家对应的时间t=10,10-9.5=0.5(h),
所以妈妈比小亮提前0.5小时到达姥姥家,故正确;
【答案】D
C.由图象可知,当t=9时,妈妈追上小亮,故正确;
D.由图象可知,当t=9时,妈妈追上小亮,此时小亮离家的时间为9-8=1(h),
所以小亮走的路程为1×12=12(km),
所以妈妈在距家12 km处追上小亮,故错误.
B
【答案】B
9.一次函数y=-3x+6的图象与y轴的交点坐标是________.
C
(0,6)
m>n
11.若点A(m,n)在直线y=kx(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的表达式为______________.
y=x或y=-x.
12.如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2 019的坐标为________________,
A2n+1的坐标为_____________________________.
((-2)n,(-1)n2n+1)(n为自然数).
(-21 009,-21 010)
13.已知y与x-3成正比例,且当x=2时,y=-3.
(1)求y与x之间的函数表达式;
解:由y与x-3成正比例,可设y=k(x-3)(k≠0),
则-3=k(2-3),所以k=3,
所以y与x之间的函数表达式为y=3(x-3),即y=3x-9.
13.已知y与x-3成正比例,且当x=2时,y=-3.
(2)求当x=1时,y的值;
(3)求当y=-6时,x的值.
把y=-3代入y=3x-9,得-3=3x-9,解得x=2.
解:把x=1代入y=3x-9,得y=3×1-9=-6.
14.已知一次函数y=kx+4(k≠0).
(1)当x=-1时,y=2,求此函数的表达式;
解:因为当x=-1时,y=2,
所以2=-k+4,解得k=2,
所以此函数的表达式为y=2x+4.
14.已知一次函数y=kx+4(k≠0).
(2)在如图所示的坐标系中画出一次函数的图象,该图象与x轴、y轴的交点分别为A、B,求出三角形AOB的面积;
14.已知一次函数y=kx+4(k≠0).
(3)利用图象求出当y≤3时,x的取值范围.
解:当y=3时,可求得x=-0.5,
由函数图象可知y随x的增大而增大,
所以当y≤3时,x≤-0.5,
即x的取值范围是x≤-0.5.
15.小东从家出发到学校参加毕业汇演,到学校时发现演出道具还放在家中,此时距毕业汇演开始还有25分,于是立即步行回家(匀速).同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.如图,线段AB、OB分别表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校
的距离S(米)与所用时间t(分)之间的函数
关系,结合图象解答下列问题.
(1)求点B坐标;
解:由图象可知父子俩从出发
到相遇用了15分,设小东步行
的速度为x米/分,则小东父亲骑车的速度为3x米/分,依题意,得15(x+3x)=3 600,解得x=60.
所以两人相遇处离学校的距离为60×15=900(米).
所以点B的坐标为(15,900).
(2)求AB所在直线的表达式;
(3)小东能否在毕业汇演开始前到达学校?
解:在S=-180t+3 600中,令S=0,
得-180t+3 600=0,解得t=20,
即小东的父亲从家到学校用的时间为20分,则小东取道具回到学校的时间为20分,
因为20<25,所以小东能在毕业汇演开始前到达学校.
16.定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
解:因为特征数为[k-1,k2-1]的一次函数
为y=(k-1)x+k2-1,
所以k2-1=0,k-1≠0,所以k=-1.
16.定义[p,q]为一次函数y=px+q的特征数.
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且三角形OAB的面积为4(O为原点),求过A,B两点的一次函数的特征数.
17.在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x(张),购票总价为y(元)):方案一,提供8 000元赞助后,每张票的票价为50元;方案二,票价按如图所示的折线OAB所表示的函数关系确定.
(1)若购买120张票,按方案一和方案二
应付的购票款分别是多少?
解:按方案一购票,应付的购票款为
8 000+50×120=14 000(元),
按方案二购票,应付的购票款为13 200元.
17.在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x(张),购票总价为y(元)):方案一,提供8 000元赞助后,每张票的票价为50元;方案二,票价按如图所示的折线OAB所表示的函数关系确定.
(2)求方案二中y与x之间的函数
表达式;
17.在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x(张),购票总价为y(元)):方案一,提供8 000元赞助后,每张票的票价为50元;方案二,票价按如图所示的折线OAB所表示的函数关系确定.
(3)至少购买多少张票时选择方案
一比较合算?
解:按方案一购票,应付的购票款为y=8 000+50x,
由(1)可知,要选择方案一比较合算,购票张数必须超过120张,则8 000+50x<60x+6 000,解得x>200,
故至少购买201张票时选择方案一比较合算.
章末小测
第12章 一次函数
答案显示
C
D
B
(0,6)
m>n
C
C
A
B
C
答案显示
(-21 009,-21 010);((-2)n,(-1)n2n+1)(n为自然数).
y=x或y=-x.
(1)y=2x+4. (2)图略.4. (3)x≤-0.5.
(1)(15,900). (2)S=-180t+3 600.
(3)小东能在毕业汇演开始前到达学校.
(1)y=3x-9. (2)y=3×1-9=-6. (3)x=2.
答案显示
(1)k=-1. (2)[-2, 4]或[-2,-4].
1.某品牌迷你豆浆机成本为70元,经销商对其销量、定价进行了统计,整理如下表,下列说法正确的是( )
C
A.定价是常量,销量是变量
B.定价是变量,销量是常量
C.定价与销量都是变量,定价是自变量,销量是因变量
D.定价与销量都是变量,销量是自变量,定价是因变量
定价/元 100 110 120 130 140 150
销量/个 80 100 110 100 80 60
C
3.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.0<k≤3
C.0≤k<3 D.0<k<3
A
4.已知一次函数y1=k1x+3和y2=k2x+2.若k1>0且k2<0,则这两个一次函数图象的交点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
5.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为( )
A.y=-x-2 B.y=-x-6
C.y=-x+10 D.y=-x-1
C
【答案】C
7.小亮家与姥姥家相距24 km,小亮8时从家出发,骑自行车去姥姥家,妈妈半小时后从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(h)的函数图象如图所示,下列结论错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5小时到达姥姥家
C.9时妈妈追上小亮
D.妈妈在距家13 km处追上小亮
【点拨】A.根据函数图象小亮去姥姥家所用时间为10-8=2(h),
所以小亮骑自行车的平均速度为24÷2=12(km/h),故正确;
B.由图象可得,妈妈到姥姥家对应的时间t=9.5,小亮到姥姥家对应的时间t=10,10-9.5=0.5(h),
所以妈妈比小亮提前0.5小时到达姥姥家,故正确;
【答案】D
C.由图象可知,当t=9时,妈妈追上小亮,故正确;
D.由图象可知,当t=9时,妈妈追上小亮,此时小亮离家的时间为9-8=1(h),
所以小亮走的路程为1×12=12(km),
所以妈妈在距家12 km处追上小亮,故错误.
B
【答案】B
9.一次函数y=-3x+6的图象与y轴的交点坐标是________.
C
(0,6)
m>n
11.若点A(m,n)在直线y=kx(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的表达式为______________.
y=x或y=-x.
12.如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2 019的坐标为________________,
A2n+1的坐标为_____________________________.
((-2)n,(-1)n2n+1)(n为自然数).
(-21 009,-21 010)
13.已知y与x-3成正比例,且当x=2时,y=-3.
(1)求y与x之间的函数表达式;
解:由y与x-3成正比例,可设y=k(x-3)(k≠0),
则-3=k(2-3),所以k=3,
所以y与x之间的函数表达式为y=3(x-3),即y=3x-9.
13.已知y与x-3成正比例,且当x=2时,y=-3.
(2)求当x=1时,y的值;
(3)求当y=-6时,x的值.
把y=-3代入y=3x-9,得-3=3x-9,解得x=2.
解:把x=1代入y=3x-9,得y=3×1-9=-6.
14.已知一次函数y=kx+4(k≠0).
(1)当x=-1时,y=2,求此函数的表达式;
解:因为当x=-1时,y=2,
所以2=-k+4,解得k=2,
所以此函数的表达式为y=2x+4.
14.已知一次函数y=kx+4(k≠0).
(2)在如图所示的坐标系中画出一次函数的图象,该图象与x轴、y轴的交点分别为A、B,求出三角形AOB的面积;
14.已知一次函数y=kx+4(k≠0).
(3)利用图象求出当y≤3时,x的取值范围.
解:当y=3时,可求得x=-0.5,
由函数图象可知y随x的增大而增大,
所以当y≤3时,x≤-0.5,
即x的取值范围是x≤-0.5.
15.小东从家出发到学校参加毕业汇演,到学校时发现演出道具还放在家中,此时距毕业汇演开始还有25分,于是立即步行回家(匀速).同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.如图,线段AB、OB分别表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校
的距离S(米)与所用时间t(分)之间的函数
关系,结合图象解答下列问题.
(1)求点B坐标;
解:由图象可知父子俩从出发
到相遇用了15分,设小东步行
的速度为x米/分,则小东父亲骑车的速度为3x米/分,依题意,得15(x+3x)=3 600,解得x=60.
所以两人相遇处离学校的距离为60×15=900(米).
所以点B的坐标为(15,900).
(2)求AB所在直线的表达式;
(3)小东能否在毕业汇演开始前到达学校?
解:在S=-180t+3 600中,令S=0,
得-180t+3 600=0,解得t=20,
即小东的父亲从家到学校用的时间为20分,则小东取道具回到学校的时间为20分,
因为20<25,所以小东能在毕业汇演开始前到达学校.
16.定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
解:因为特征数为[k-1,k2-1]的一次函数
为y=(k-1)x+k2-1,
所以k2-1=0,k-1≠0,所以k=-1.
16.定义[p,q]为一次函数y=px+q的特征数.
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且三角形OAB的面积为4(O为原点),求过A,B两点的一次函数的特征数.
17.在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x(张),购票总价为y(元)):方案一,提供8 000元赞助后,每张票的票价为50元;方案二,票价按如图所示的折线OAB所表示的函数关系确定.
(1)若购买120张票,按方案一和方案二
应付的购票款分别是多少?
解:按方案一购票,应付的购票款为
8 000+50×120=14 000(元),
按方案二购票,应付的购票款为13 200元.
17.在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x(张),购票总价为y(元)):方案一,提供8 000元赞助后,每张票的票价为50元;方案二,票价按如图所示的折线OAB所表示的函数关系确定.
(2)求方案二中y与x之间的函数
表达式;
17.在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x(张),购票总价为y(元)):方案一,提供8 000元赞助后,每张票的票价为50元;方案二,票价按如图所示的折线OAB所表示的函数关系确定.
(3)至少购买多少张票时选择方案
一比较合算?
解:按方案一购票,应付的购票款为y=8 000+50x,
由(1)可知,要选择方案一比较合算,购票张数必须超过120张,则8 000+50x<60x+6 000,解得x>200,
故至少购买201张票时选择方案一比较合算.
