人教版高一物理必修二 第六章6.4万有引力理论的成就(23张ppt 海南省国兴中学2020年
文档属性
| 名称 | 人教版高一物理必修二 第六章6.4万有引力理论的成就(23张ppt 海南省国兴中学2020年 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-21 09:20:06 | ||
图片预览






文档简介
(共23张PPT)
课前检测
(1)物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
(2)万有引力定律的内容是什么?如何用公式表示?
(3)重力和万有引力的关系?
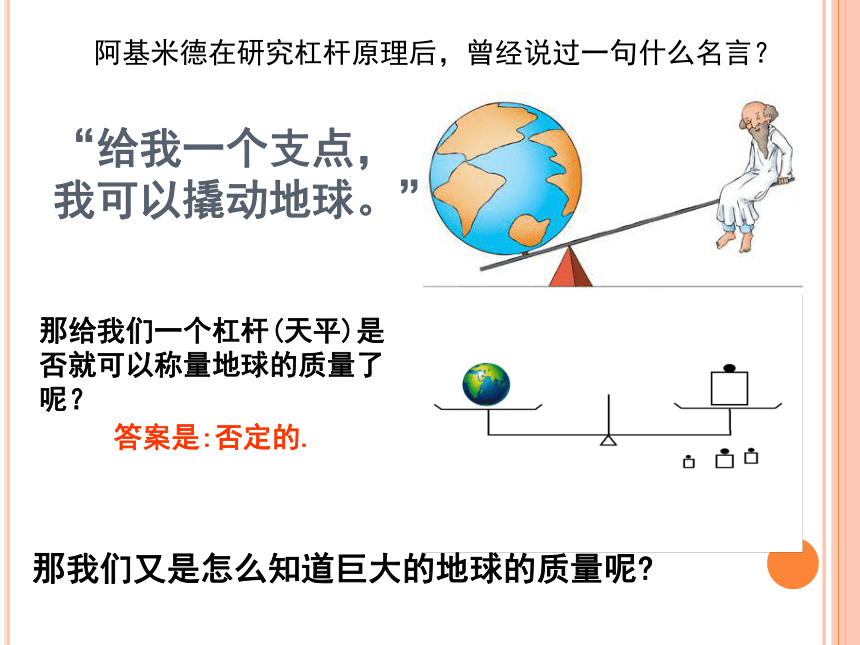
讨论:地球表面物体的重力与地球对物体的万有引力的关系。
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。
讨论:地球表面物体的重力与地球对物体的万有引力的关系。
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。
因此,重力是万有引力的一个分力。
实际上随地球自转的物体向心力远小于重力,在忽略自转的影响下万有引力大小近似等于重力大小。
(1)物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
(2)万有引力定律的内容是什么?如何用公式表示?
(3)重力和万有引力的关系?
重力是万有引力的一个分力,当忽略了地球的自转时,可认为重力在数值上就等于万有引力大小。
课前检测
阿基米德在研究杠杆原理后,曾经说过一句什么名言?
“给我一个支点,我可以撬动地球。”
那我们又是怎么知道巨大的地球的质量呢?
那给我们一个杠杆(天平)是否就可以称量地球的质量了呢?
答案是:否定的.
一、称量地球的质量
地球的质量不可能用天平称量.
但是万有引力定律是否能给予我们提供帮助呢?
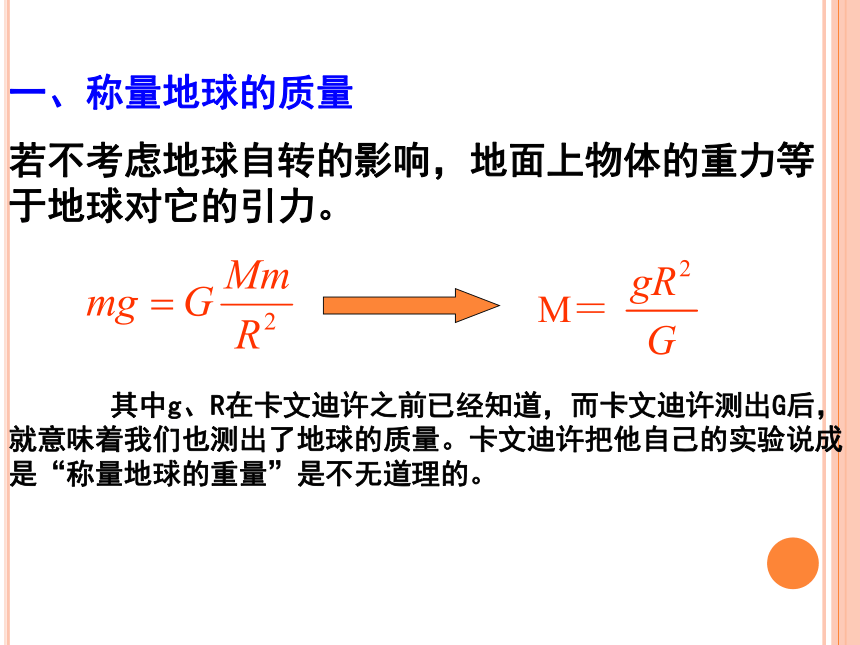
一、称量地球的质量
若不考虑地球自转的影响,地面上物体的重力等于地球对它的引力。
其中g、R在卡文迪许之前已经知道,而卡文迪许测出G后,就意味着我们也测出了地球的质量。卡文迪许把他自己的实验说成是“称量地球的重量”是不无道理的。
一、称量地球的质量
通过万有引力定律称量地球的质量,这不能不说是一个奇迹。
就连一个外行人、著名文学家马克·吐温满怀激情地说:
“科学真是迷人。根据零星的事实,增添一点猜想,竟能赢得那么多收获!”
这话虽然出自一位外行人之口,却道出了科学发现的精髓。
二、天体质量的计算
1、地球公转实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
思考:
应用万有引力可算出地球的质量,能否算出太阳的质量呢?
分析问题:
1、地球实际作何运动?而我们通常可以认为做什么运动?
地球实际轨道是椭圆,通常可以认为地球绕太阳做匀速圆周运动
二、天体质量的计算
1、地球实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
2、地球作圆周运动的向心力是由什么力来提供的?
思考:
应用万有引力可算出地球的质量,能否算出太阳的质量呢?
通常可以认为地球绕太阳做匀速圆周运动
2、地球作圆周运动的向心力是由什么力来提供的?
地球作圆周运动的向心力是由太阳对地球的万有引力来提供的
二、天体质量的计算
1、地球实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
2、地球作圆周运动的向心力是由什么力来提供的?
思考:
应用万有引力可算出地球的质量,能否算出太阳的质量呢?
通常可以认为地球绕太阳做匀速圆周运动
地球做圆周运动的向心力是由太阳对地球的万有引力来提供的
地球作圆周运动的向心力是由太阳对地球的万有引力来提供的
该表达式与地球(环绕天体)质量m有没有关系?
总结推广
求解思路:
环绕天体的向心力由中心天体对其万有引力独家提供
具体方法:
特点:
须知道待求天体(M)的某一环行天体的运行规律,
且与环行天体的质量(m)无关.
二、计算天体的质量
学以致用
计算地球的质量,除了一开始的方法外,还可以怎么求?
借助于月球,那么需要知道哪些量?
月球绕地球运行的周期T=27.3天,
月球与地球的平均距离r=3.84×108m
M=5.98×1024kg
思考讨论
2.若需要测定木星的平均密度,需要测量哪些物理量?
1.木星是绕太阳公转的行星之一,而木星周围又有卫星绕它转动如果要测木星的质量需要测量哪些量?
设木星星球为密度均匀的球体,则由体积公式
及时练习1
若已知宇宙飞船绕海王星运动的轨道半径为r,周期为T,引力常量为G,则由此可求出 ( ) A、行星的质量
B、太阳的质量
C、行星的密度
D、太阳的密度
B
你知道当初人们是如何发现海王星的吗?
发现天王星轨道偏离
1846年9月23日晚,由德国的伽勒在柏林天文台用望远镜在勒维耶预言的位置附近发现了这颗行星——海王星
柏林天文台
四、小结
这节课我们主要掌握的知识点是:
1.万有引力定律在天文学中的应用,一般有两条思路:
(2) 环绕天体所需的向心力由中心天体对环绕天体的万有引力提供
(1) 地面(或某星球表面)的物体的重力近似等于万有引力
2.了解了万有引力定律在天文学中具有的重要意义.
课前检测
(1)物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
(2)万有引力定律的内容是什么?如何用公式表示?
(3)重力和万有引力的关系?
讨论:地球表面物体的重力与地球对物体的万有引力的关系。
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。
讨论:地球表面物体的重力与地球对物体的万有引力的关系。
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。
因此,重力是万有引力的一个分力。
实际上随地球自转的物体向心力远小于重力,在忽略自转的影响下万有引力大小近似等于重力大小。
(1)物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
(2)万有引力定律的内容是什么?如何用公式表示?
(3)重力和万有引力的关系?
重力是万有引力的一个分力,当忽略了地球的自转时,可认为重力在数值上就等于万有引力大小。
课前检测
阿基米德在研究杠杆原理后,曾经说过一句什么名言?
“给我一个支点,我可以撬动地球。”
那我们又是怎么知道巨大的地球的质量呢?
那给我们一个杠杆(天平)是否就可以称量地球的质量了呢?
答案是:否定的.
一、称量地球的质量
地球的质量不可能用天平称量.
但是万有引力定律是否能给予我们提供帮助呢?
一、称量地球的质量
若不考虑地球自转的影响,地面上物体的重力等于地球对它的引力。
其中g、R在卡文迪许之前已经知道,而卡文迪许测出G后,就意味着我们也测出了地球的质量。卡文迪许把他自己的实验说成是“称量地球的重量”是不无道理的。
一、称量地球的质量
通过万有引力定律称量地球的质量,这不能不说是一个奇迹。
就连一个外行人、著名文学家马克·吐温满怀激情地说:
“科学真是迷人。根据零星的事实,增添一点猜想,竟能赢得那么多收获!”
这话虽然出自一位外行人之口,却道出了科学发现的精髓。
二、天体质量的计算
1、地球公转实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
思考:
应用万有引力可算出地球的质量,能否算出太阳的质量呢?
分析问题:
1、地球实际作何运动?而我们通常可以认为做什么运动?
地球实际轨道是椭圆,通常可以认为地球绕太阳做匀速圆周运动
二、天体质量的计算
1、地球实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
2、地球作圆周运动的向心力是由什么力来提供的?
思考:
应用万有引力可算出地球的质量,能否算出太阳的质量呢?
通常可以认为地球绕太阳做匀速圆周运动
2、地球作圆周运动的向心力是由什么力来提供的?
地球作圆周运动的向心力是由太阳对地球的万有引力来提供的
二、天体质量的计算
1、地球实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
2、地球作圆周运动的向心力是由什么力来提供的?
思考:
应用万有引力可算出地球的质量,能否算出太阳的质量呢?
通常可以认为地球绕太阳做匀速圆周运动
地球做圆周运动的向心力是由太阳对地球的万有引力来提供的
地球作圆周运动的向心力是由太阳对地球的万有引力来提供的
该表达式与地球(环绕天体)质量m有没有关系?
总结推广
求解思路:
环绕天体的向心力由中心天体对其万有引力独家提供
具体方法:
特点:
须知道待求天体(M)的某一环行天体的运行规律,
且与环行天体的质量(m)无关.
二、计算天体的质量
学以致用
计算地球的质量,除了一开始的方法外,还可以怎么求?
借助于月球,那么需要知道哪些量?
月球绕地球运行的周期T=27.3天,
月球与地球的平均距离r=3.84×108m
M=5.98×1024kg
思考讨论
2.若需要测定木星的平均密度,需要测量哪些物理量?
1.木星是绕太阳公转的行星之一,而木星周围又有卫星绕它转动如果要测木星的质量需要测量哪些量?
设木星星球为密度均匀的球体,则由体积公式
及时练习1
若已知宇宙飞船绕海王星运动的轨道半径为r,周期为T,引力常量为G,则由此可求出 ( ) A、行星的质量
B、太阳的质量
C、行星的密度
D、太阳的密度
B
你知道当初人们是如何发现海王星的吗?
发现天王星轨道偏离
1846年9月23日晚,由德国的伽勒在柏林天文台用望远镜在勒维耶预言的位置附近发现了这颗行星——海王星
柏林天文台
四、小结
这节课我们主要掌握的知识点是:
1.万有引力定律在天文学中的应用,一般有两条思路:
(2) 环绕天体所需的向心力由中心天体对环绕天体的万有引力提供
(1) 地面(或某星球表面)的物体的重力近似等于万有引力
2.了解了万有引力定律在天文学中具有的重要意义.
