黑龙江省哈尔滨市2019-2020学年第二学期九年级数学4月阶段测试题(word版无答案)
文档属性
| 名称 | 黑龙江省哈尔滨市2019-2020学年第二学期九年级数学4月阶段测试题(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 299.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 10:54:27 | ||
图片预览

文档简介
2019-2020学年第二学期初四阶段测试题
一、选择题(每题3分,共计30分)
1.我市4月份某天的最高气温是15℃,最低气温是-2℃,那么这天的温差(最高气温减最低气温)是( )
A.-13℃ B.13℃ C.-17℃ D.17℃
2.下列计算正确的是( )
A.x+x2=x3 B.2x+3x=5x2 C.(x2)3=x6 D.x6÷x3=x2
3.下列LOGO标志中,是中心对称图形,但不是轴对称图形的是( )
A. B. C. D.
4.已知反比例函数的图象位于第一、第三象限,则k的取值范围是( )
A.k>2 B.k≥2 C.k≤2 D.k<2
5.如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )
6.如图,王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地 ( ).
A .m B .100 m C. 150m D. m
7. 把抛物线向右平移2个单位,然后向下平移6个单位,则平移后抛物线的解析式为( ).
A. B. C. D.
8.某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人.则选出的恰为一男一女的概率是( )
A. B. C. D.
9.如图,在□ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是 ( ).
A. B.
C. D.
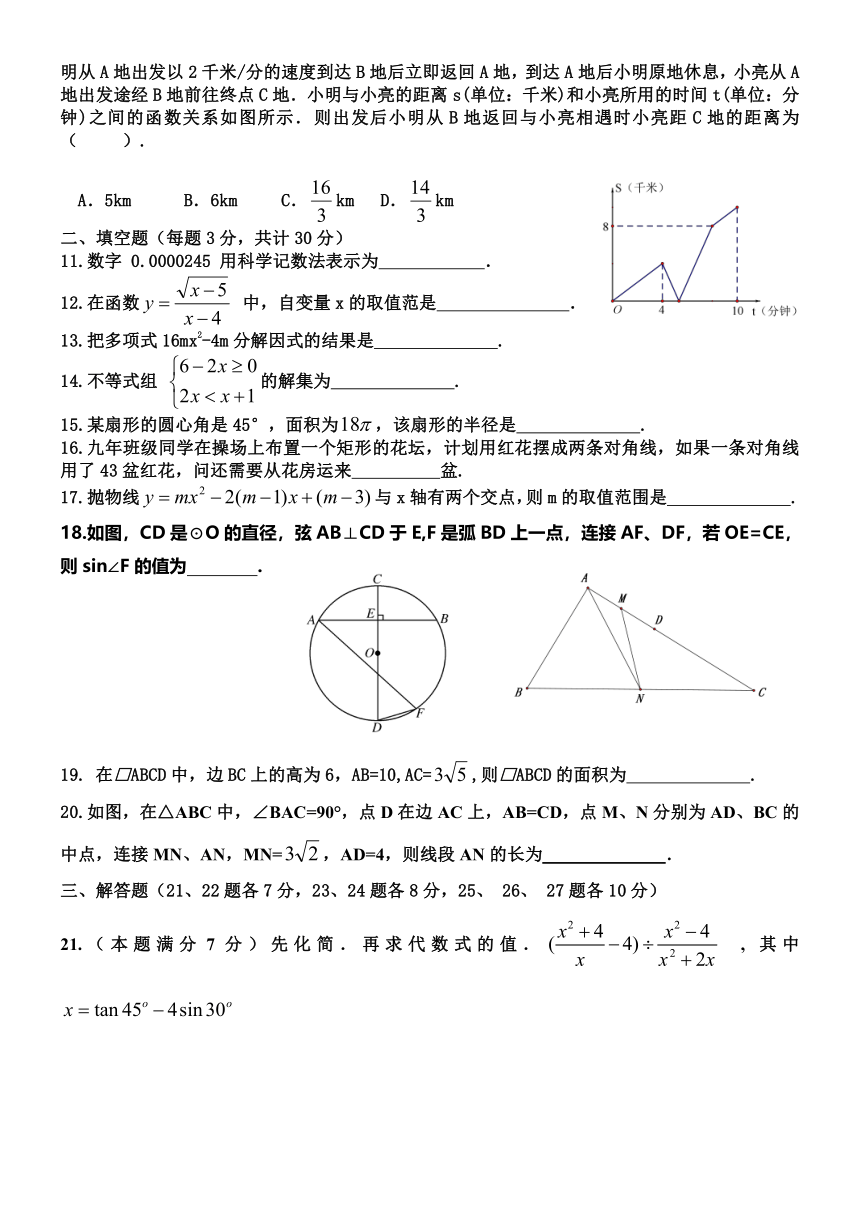
10.在一条笔直的公路上,依次有A、B、C三地.小明、小亮从A地驾车同时出发匀速运动。小明从A地出发以2千米/分的速度到达B地后立即返回A地,到达A地后小明原地休息,小亮从A地出发途经B地前往终点C地.小明与小亮的距离s(单位:千米)和小亮所用的时间t(单位:分钟)之间的函数关系如图所示.则出发后小明从B地返回与小亮相遇时小亮距C地的距离为( ).
A.5km B.6km C.km D.km
二、填空题(每题3分,共计30分)
11.数字 0.0000245 用科学记数法表示为 .
12.在函数 中,自变量x的取值范是 .
13.把多项式16mx2-4m分解因式的结果是 .
14.不等式组 的解集为 .
15.某扇形的圆心角是45°,面积为,该扇形的半径是 .
16.九年班级同学在操场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了43盆红花,问还需要从花房运来 盆.
17.抛物线与x轴有两个交点,则m的取值范围是 .
18.如图,CD是⊙O的直径,弦AB⊥CD于E,F是弧BD上一点,连接AF、DF,若OE=CE,则sin∠F的值为 .
在□ABCD中,边BC上的高为6,AB=10,AC=,则□ABCD的面积为 .
20.如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=,AD=4,则线段AN的长为 .
三、解答题(21、22题各7分,23、24题各8分,25、 26、 27题各10分)
21.(本题满分7分)先化简.再求代数式的值. , 其中
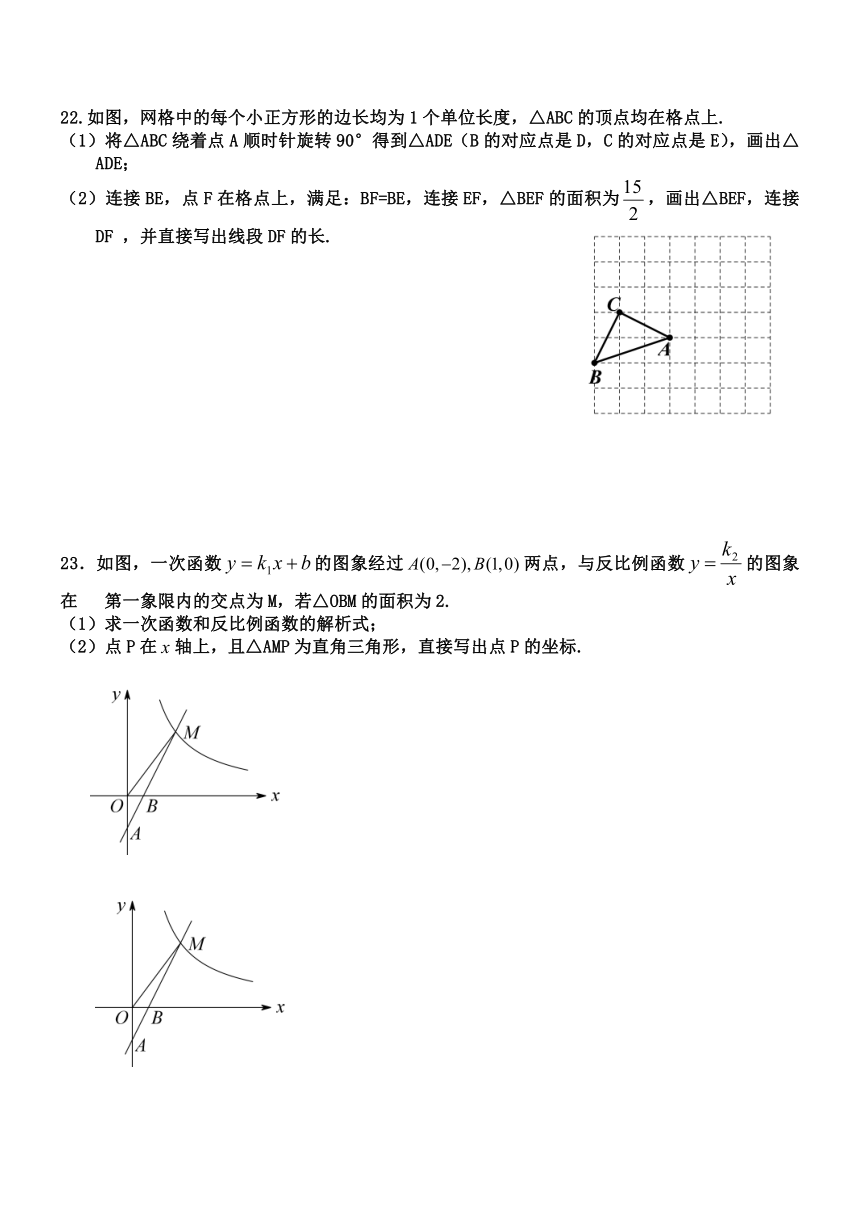
22.如图,网格中的每个小正方形的边长均为1个单位长度,△ABC的顶点均在格点上.
(1)将△ABC绕着点A顺时针旋转90°得到△ADE(B的对应点是D,C的对应点是E),画出△ADE;
(2)连接BE,点F在格点上,满足:BF=BE,连接EF,△BEF的面积为,画出△BEF,连接DF ,并直接写出线段DF的长.
23.如图,一次函数的图象经过两点,与反比例函数的图象在 第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的解析式;
(2)点P在轴上,且△AMP为直角三角形,直接写出点P的坐标.
24. 在△ABC中,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC与CE的延长线相交于点F,连接BF.
(1)如图1,求证:四边形BDAF是平行四边形;
(2)如图2,若∠ACD=90°,请写出图中所有的等腰三角形.
某公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
求购买该品牌一个台灯、一个手电筒各需要多少元;
经商谈,商店给予此公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果此公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么此公司最多可购买多少个该品牌台灯?
26.如图,在⊙O中,直径AB交弦CD于点E,连接OD.
(1)如图1,求证:∠BED=2∠ABC+∠CDO;
(2) 如图2,弦MN的延长线交CD的延长线于点R,弧BM=弧BN,∠CRM+∠ABC=45°,求证:OD∥MR;
(3)如图3,在(2)的条件下,在RM的延长线上取点T,连接BT,CB与RT交于点G,若∠RTB=∠ABC,CG=BT,,AE=,求RN的长.
27.如图,抛物线交x轴于A、B,交y轴于点C,点P在x轴下方的抛物线上,且.
求点P的横坐标;
点Q为抛物线第一象限上一点,过点P作y轴的平行线分别交BC、QC于点D、E,若CE=QE,DE=2PD,求抛物线的解析式;
在(2)的条件下,点R为y轴上一点,若CQR=2CPR,求点R的坐标.
一、选择题(每题3分,共计30分)
1.我市4月份某天的最高气温是15℃,最低气温是-2℃,那么这天的温差(最高气温减最低气温)是( )
A.-13℃ B.13℃ C.-17℃ D.17℃
2.下列计算正确的是( )
A.x+x2=x3 B.2x+3x=5x2 C.(x2)3=x6 D.x6÷x3=x2
3.下列LOGO标志中,是中心对称图形,但不是轴对称图形的是( )
A. B. C. D.
4.已知反比例函数的图象位于第一、第三象限,则k的取值范围是( )
A.k>2 B.k≥2 C.k≤2 D.k<2
5.如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )
6.如图,王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地 ( ).
A .m B .100 m C. 150m D. m
7. 把抛物线向右平移2个单位,然后向下平移6个单位,则平移后抛物线的解析式为( ).
A. B. C. D.
8.某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人.则选出的恰为一男一女的概率是( )
A. B. C. D.
9.如图,在□ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是 ( ).
A. B.
C. D.
10.在一条笔直的公路上,依次有A、B、C三地.小明、小亮从A地驾车同时出发匀速运动。小明从A地出发以2千米/分的速度到达B地后立即返回A地,到达A地后小明原地休息,小亮从A地出发途经B地前往终点C地.小明与小亮的距离s(单位:千米)和小亮所用的时间t(单位:分钟)之间的函数关系如图所示.则出发后小明从B地返回与小亮相遇时小亮距C地的距离为( ).
A.5km B.6km C.km D.km
二、填空题(每题3分,共计30分)
11.数字 0.0000245 用科学记数法表示为 .
12.在函数 中,自变量x的取值范是 .
13.把多项式16mx2-4m分解因式的结果是 .
14.不等式组 的解集为 .
15.某扇形的圆心角是45°,面积为,该扇形的半径是 .
16.九年班级同学在操场上布置一个矩形的花坛,计划用红花摆成两条对角线,如果一条对角线用了43盆红花,问还需要从花房运来 盆.
17.抛物线与x轴有两个交点,则m的取值范围是 .
18.如图,CD是⊙O的直径,弦AB⊥CD于E,F是弧BD上一点,连接AF、DF,若OE=CE,则sin∠F的值为 .
在□ABCD中,边BC上的高为6,AB=10,AC=,则□ABCD的面积为 .
20.如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=,AD=4,则线段AN的长为 .
三、解答题(21、22题各7分,23、24题各8分,25、 26、 27题各10分)
21.(本题满分7分)先化简.再求代数式的值. , 其中
22.如图,网格中的每个小正方形的边长均为1个单位长度,△ABC的顶点均在格点上.
(1)将△ABC绕着点A顺时针旋转90°得到△ADE(B的对应点是D,C的对应点是E),画出△ADE;
(2)连接BE,点F在格点上,满足:BF=BE,连接EF,△BEF的面积为,画出△BEF,连接DF ,并直接写出线段DF的长.
23.如图,一次函数的图象经过两点,与反比例函数的图象在 第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的解析式;
(2)点P在轴上,且△AMP为直角三角形,直接写出点P的坐标.
24. 在△ABC中,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC与CE的延长线相交于点F,连接BF.
(1)如图1,求证:四边形BDAF是平行四边形;
(2)如图2,若∠ACD=90°,请写出图中所有的等腰三角形.
某公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
求购买该品牌一个台灯、一个手电筒各需要多少元;
经商谈,商店给予此公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果此公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么此公司最多可购买多少个该品牌台灯?
26.如图,在⊙O中,直径AB交弦CD于点E,连接OD.
(1)如图1,求证:∠BED=2∠ABC+∠CDO;
(2) 如图2,弦MN的延长线交CD的延长线于点R,弧BM=弧BN,∠CRM+∠ABC=45°,求证:OD∥MR;
(3)如图3,在(2)的条件下,在RM的延长线上取点T,连接BT,CB与RT交于点G,若∠RTB=∠ABC,CG=BT,,AE=,求RN的长.
27.如图,抛物线交x轴于A、B,交y轴于点C,点P在x轴下方的抛物线上,且.
求点P的横坐标;
点Q为抛物线第一象限上一点,过点P作y轴的平行线分别交BC、QC于点D、E,若CE=QE,DE=2PD,求抛物线的解析式;
在(2)的条件下,点R为y轴上一点,若CQR=2CPR,求点R的坐标.
同课章节目录
