【备战2020】中考数学二轮专题 图形运动中的不变关系问题复习学案(上海地区专用)
文档属性
| 名称 | 【备战2020】中考数学二轮专题 图形运动中的不变关系问题复习学案(上海地区专用) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 20:25:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
备战2020中考数学二轮专题复习学案
图形运动中的不变关系问题
【备注】本部分为知识点和基本方法梳理,引导学生回顾总结,大概5分钟左右
一.图形运动中的不变关系常见题型:
二.题型特征和解题思路:
【备注】:
以下每题教法建议,请老师根据学生实际情况参考;
在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;
可以根据各题的“参考教法”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;
例题讲解,可以根据“参考教法”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;
引导的技巧:直接提醒,问题式引导,类比式引导等等;
部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;
每个题目的讲解时间根据实际情况处理,建议每题6-9分钟。
三、典型例题
例1.如图,已知AB⊥MN,垂足为点B,P是射线BN上的一个动点,AC⊥AP,∠ACP=∠BAP,AB=4,BP=x,CP=y,点C到MN的距离为线段CD的长。(★★★★★)
(1)求y关于x的函数解析式,并写出它的定义域.
(2)在点P的运动过程中,点C到MN的距离是否会发生变化?如果发生变化,请用x的代数式表示这段距离;如果不发生变化,请求出这段距离。
【参考教法】可参考以下方法引导学生分析问题、解决问题
一.寻找题目中的已知量和特殊条件:
1.哪些边已知?哪些边存在特殊关系? 提示:AB=4、AB⊥MN、AC⊥AP;
2.角的关系。直角和等角产生了很多角度相等,让学生找找看,为后面的相似做好前提。
求解函数关系式:用相似产生的比例关系即可证明。
证明线段的长度是否会发生变化:
方案一.直接求解改线段的长度;方案二.证明该线段的长度随着点的运动在不断的变化
本题寻找方案一,直接计算求解的长度。延长交于点,证明是的中位线即可。
【满分解答】(1)∵AB⊥MN,AC⊥AP,∴.
又∵∠ACP=∠BAP,∴△ABP∽△CAP.
∴,即.
∴所求的函数解析式为 .
(2)CD的长不会发生变化.
延长CA交直线MN于点E.
∵AC⊥AP,∴.
∵∠ACP=∠BAP,∴.∴.
∴. ∴.
∵,,
∴.
∴.
∵AB=4,∴.
对应练习:
1.
(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图8);
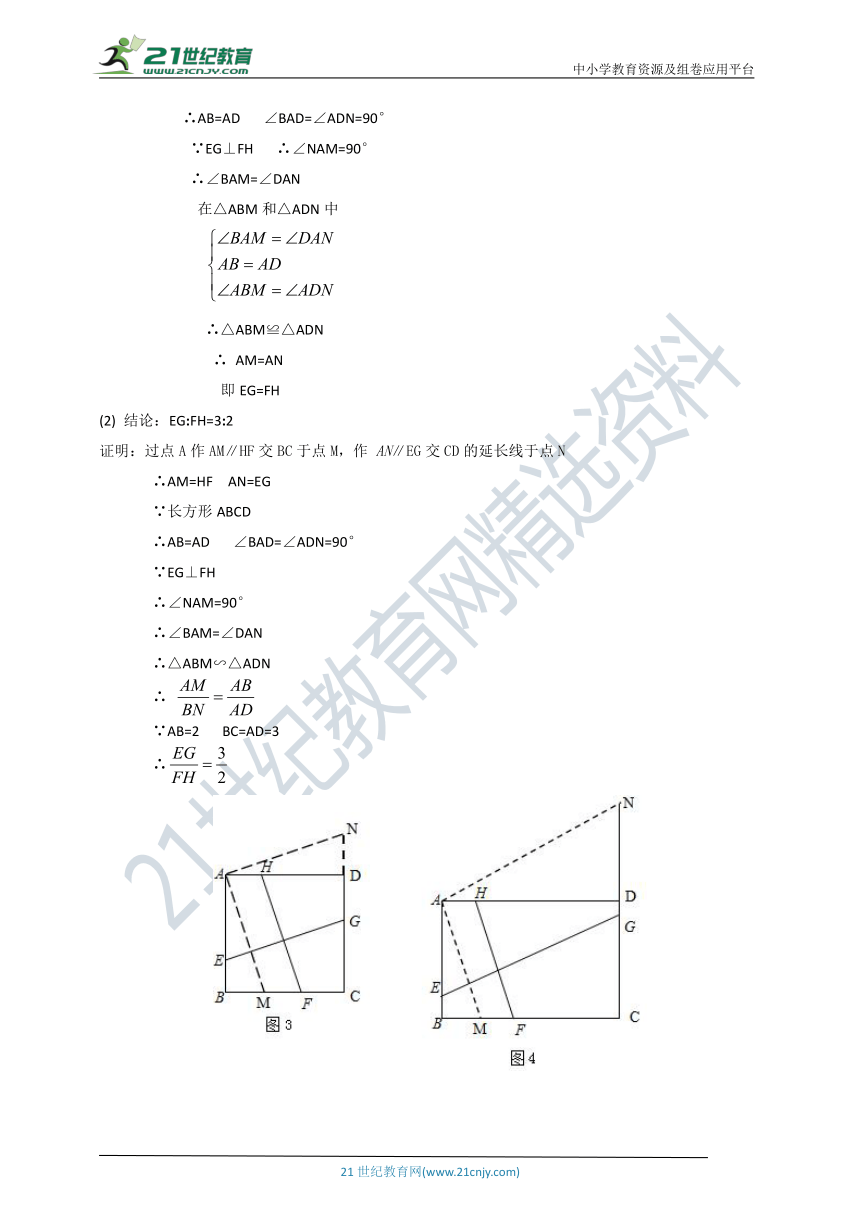
(2)如果把条件中的“正方形”改为“长方形”,并设AB =2,BC =3(如图9),试探究EG、FH之间有怎样的数量关系,并证明你的结论。(★★★★)
【解法点拨】可以参考以下方法分析问题、解决问题:
一.寻找题目中的已知量和特殊条件:
1.特殊图形:正方形或者矩形
2.边的关系:
二.求解边的大小关系:
方案一.转化为证明全等三角形;
方案二.直接计算求解每一条线段的长度,在寻找关系。
【满分解答】
证明:过点A作AM∥HF交BC于点M,作 AN∥EG交CD的延长线于点N
∴AM=HF AN=EG
∵正方形ABCD
∴AB=AD ∠BAD=∠ADN=90°
∵EG⊥FH ∴∠NAM=90°
∴∠BAM=∠DAN
在△ABM和△ADN中
∴△ABM≌△ADN
∴ AM=AN
即EG=FH
(2) 结论:EG:FH=3:2
证明:过点A作AM∥HF交BC于点M,作 AN∥EG交CD的延长线于点N
∴AM=HF AN=EG
∵长方形ABCD
∴AB=AD ∠BAD=∠ADN=90°
∵EG⊥FH
∴∠NAM=90°
∴∠BAM=∠DAN
∴△ABM∽△ADN
∴
∵AB=2 BC=AD=3
∴
例2.如图,已知,点是内一点,,垂足为点,,,是延长线上一点,联结并延长与射线交于点。设,是否存在适当的,使得,若存在,试求出的值;若不存在,试说明理由。(★★★★★)
?N
B
O
C
P
A
M
?
【参考教法】可参考以下教法引导学生分析问题、解决问题
寻找题目中的已知量和特殊条件:
1.哪些边已知?哪些边存在特殊关系? 提示:,,
2.角的关系? 提示:
二.求解面积比与边长比的关系:
1.两个图形的面积分别是什么图形? 提示:和四边形。
2.怎么求解? 提示:画高直接求。
3.设边的长度计算求解。
【满分解答】
设,OE=,则
由
设CA=x,则
∴
∵
若由,得,
则
∴ (舍去)
∴
【备注】:本部分对前面例题中讲到的解题方法进行归类总结,以引导式总结出,建议时间4分钟左右。
四、规律总结
五、实战演练:
【备注】该部分需要学生在10分钟内独立完成,满分10分,之后再评分并讲评
如图,在△中,是上一点,是上一点, .求证:(1)∥; (2)。(10分)(★★★★)
【解法点拨】可以参考一下方法引导学生分析问题、解决问题
寻找题目中的已知量和特殊条件:
1.边:
2.角:
3.特殊图形:形成相似基本型。
二.证明平行线,用相似证明角度相等即可。
证明,转化为之比,求解。
【满分解答】
(1)证明:∵,
∴.
∵∠为公共角.
∴△∽. (2分)
∴. (1分)
∵,
∴. (1分)
∴∥. (1分)
(2)证明:∵∥,
∴△∽△.
∴. (2分)
∵∥,
∴△与△同高.
∴. (2分)
∴. (1分)
在中,点为边边上的一动点,点在线段上,过点作、,与边、分别交于点、。求证:。(8分)
(★★★★★)
【解法点拨】可参考以下方向引导学生分析问题、解决问题:
寻找题目中的已知量和特殊关系:
边:、;
基本图形:、,形成平行四边形和相似基本图形。
证明边的比值关系:
添加辅助线构造基本图形,延长交边于点;
和,在结合线段的和差关系即可证明。
【满分解答】:延长交边于点,则
因为、,则四边形为平行四边形.............................1分
∵
∴
∴...................................3分
又∵
∴.............................................................................2分
∴.............................................................................1分
∴........................................................................1分
A
B
P
D
C
N
M
小杰和他的同学组成了“爱琢磨”学习小组,有一次,他们碰到这样一道题:
“已知正方形ABCD ,点E、F、G、H分别在边AB、BC、CD、DA上,若EG⊥FH,则EG = FH”
经过思考,大家给出了以下两个方案:
(甲)过点A作AM∥HF交BC于点M,过点B作BN∥EG交CD于点N ;
(乙)过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N ;
小杰和他的同学顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索。
……
图形运动中的不变关系问题的解题方法和策略:
1.寻找题目中的已知量和不变量;
2.观察所求不变量与动点的关系;
3.通过点、线的运动进行证明或计算;
4.利用好相似基本型和勾股定理;
5.抓住变换特征,并研究内在联系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
