2020鲁教版五四制七上数学1.5利用三角形全等测距离课件(18章ppt)
文档属性
| 名称 | 2020鲁教版五四制七上数学1.5利用三角形全等测距离课件(18章ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 11:14:42 | ||
图片预览




文档简介
课件18张PPT。5 利用三角形全等测距离1. 会利用三角形全等测距离.
2. 能在解决实际问题的过程中进行有条理的思考和表述.
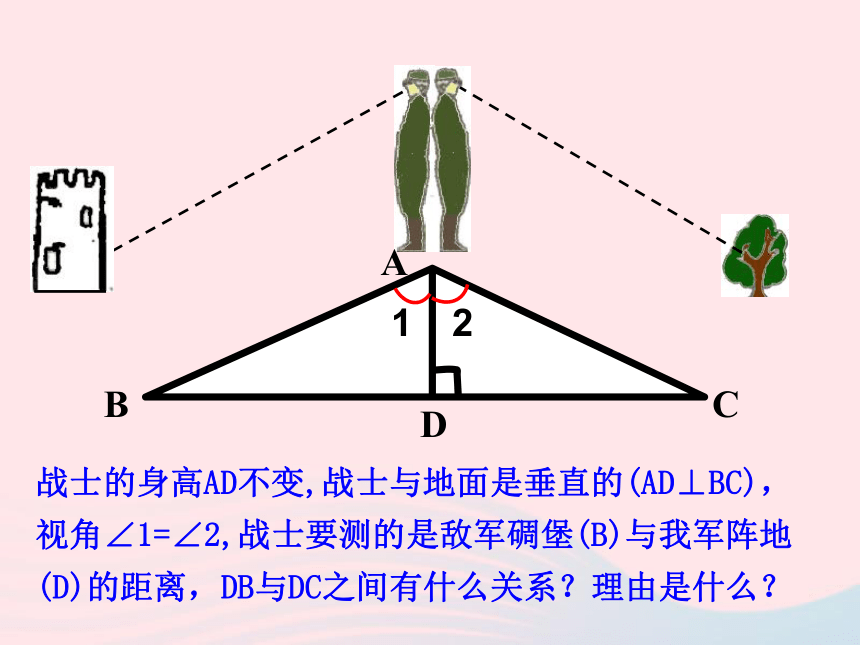
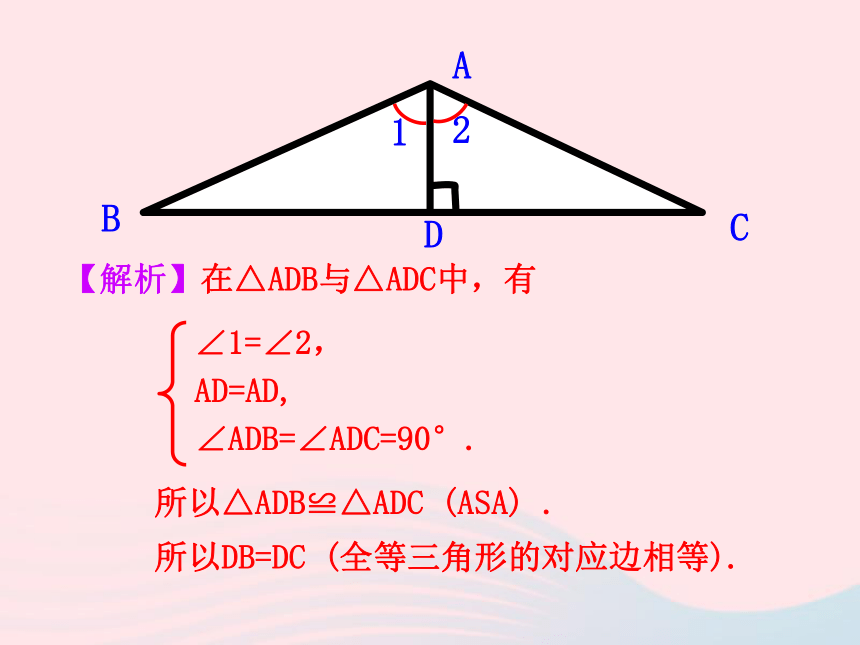
3. 体会数学与生活的密切联系,能够利用三角形全等解决生活中的实际问题. 1.全等三角形具有什么性质?对应边相等,对应角相等.2.判定两个三角形全等的条件有哪些?(1)“SSS”:三边分别相等的两个三角形全等.(2)“ASA”:两角及其的夹边分别相等的两个三角 形全等.(3)“AAS”:两角分别相等且其中一组等角的对边相等的两个三角形全等.(4)“SAS”:两边及其夹角分别相等的两个三角形全等.下面是一位经历过战争的老人讲述的一个故事: 在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢? 一个战士想出来这样一个办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.12ABDC战士的身高AD不变,战士与地面是垂直的(AD⊥BC),视角∠1=∠2,战士要测的是敌军碉堡(B)与我军阵地(D)的距离,DB与DC之间有什么关系?理由是什么?12ABDC【解析】在△ADB与△ADC中,有 ∠1=∠2,
AD=AD,
∠ADB=∠ADC=90°.所以△ADB≌△ADC (ASA) .所以DB=DC (全等三角形的对应边相等).【例】A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长.【例题】 一位叔叔帮小明出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.CDEAB=DE,你能说出理由来吗?在△CED与△CBA中,有 CE=CB,
∠ECD=∠BCA,
CD=CA.所以△CED≌△CBA (SAS) .所以DE=AB
(全等三角形的对应边相等).方法一:【解析】ABCDE ∠ B=∠EDC,
BC=DC,
∠ACB=∠ECD,所以 △ABC≌△EDC(ASA),所以AB=ED在△ABC与△EDC中,有(全等三角形的对应边相等)方法二:1.如图,太阳光线AC与A′C′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由?【解析】一样长,理由如下:因为AC∥A C ,所以∠ACB=∠A C B
(两直线平行,同位角相等).′′′所以BC =B C (全等三角形的对应边相等).′′所以△ABC≌△A B C(AAS).′′′ ∠ABC=∠A B C =90°,
∠ACB=∠A C B ,
AB=A B .′′′′′′′′在△ABC和△A B C 中,有′′′′′2.如图所示,小明设计了一种测工件内径AB的卡钳
(只要测出CD,就知道AB),问:在卡钳的设计中,AO,
BO,CO,DO 应满足下列的哪个条件( )
(A)AO=CO
(B)BO=DO
(C)AC=BD
(D)AO=CO且BO=DOD3.(威海·中考)在△ABC中,AB>AC,
点D,E分别是边AB,AC的中点,点F在
BC边上,连接DE,DF,EF,则添加下
列哪一个条件后,仍无法判定△BFD
与△EDF全等( )
(A)EF∥AB (B)BF=CF
(C)∠A=∠DFE (D)∠B=∠DEF【解析】选C.因为当EF∥AB时,四边形BDEF是平行四边形,△BFD≌△EDF;当BF=CF时,点F为BC的中点,四边形BDEF是平行四边形,△BFD≌△EDF;当∠B=∠DEF时,因为DE∥BC,∠DEF=∠EFC,所以∠B=∠EFC,EF∥AB, 四边形BDEF是平行四边形,△BFD≌△EDF.(2)运用所学有关知识设计合适可行的方案,并说明理由.(1)应用三角形全等测量距离(构造全等三角形). 通过本课时的学习,需要我们掌握:海到天边天作岸,山登绝顶我为峰.
2. 能在解决实际问题的过程中进行有条理的思考和表述.
3. 体会数学与生活的密切联系,能够利用三角形全等解决生活中的实际问题. 1.全等三角形具有什么性质?对应边相等,对应角相等.2.判定两个三角形全等的条件有哪些?(1)“SSS”:三边分别相等的两个三角形全等.(2)“ASA”:两角及其的夹边分别相等的两个三角 形全等.(3)“AAS”:两角分别相等且其中一组等角的对边相等的两个三角形全等.(4)“SAS”:两边及其夹角分别相等的两个三角形全等.下面是一位经历过战争的老人讲述的一个故事: 在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢? 一个战士想出来这样一个办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.12ABDC战士的身高AD不变,战士与地面是垂直的(AD⊥BC),视角∠1=∠2,战士要测的是敌军碉堡(B)与我军阵地(D)的距离,DB与DC之间有什么关系?理由是什么?12ABDC【解析】在△ADB与△ADC中,有 ∠1=∠2,
AD=AD,
∠ADB=∠ADC=90°.所以△ADB≌△ADC (ASA) .所以DB=DC (全等三角形的对应边相等).【例】A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长.【例题】 一位叔叔帮小明出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.CDEAB=DE,你能说出理由来吗?在△CED与△CBA中,有 CE=CB,
∠ECD=∠BCA,
CD=CA.所以△CED≌△CBA (SAS) .所以DE=AB
(全等三角形的对应边相等).方法一:【解析】ABCDE ∠ B=∠EDC,
BC=DC,
∠ACB=∠ECD,所以 △ABC≌△EDC(ASA),所以AB=ED在△ABC与△EDC中,有(全等三角形的对应边相等)方法二:1.如图,太阳光线AC与A′C′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由?【解析】一样长,理由如下:因为AC∥A C ,所以∠ACB=∠A C B
(两直线平行,同位角相等).′′′所以BC =B C (全等三角形的对应边相等).′′所以△ABC≌△A B C(AAS).′′′ ∠ABC=∠A B C =90°,
∠ACB=∠A C B ,
AB=A B .′′′′′′′′在△ABC和△A B C 中,有′′′′′2.如图所示,小明设计了一种测工件内径AB的卡钳
(只要测出CD,就知道AB),问:在卡钳的设计中,AO,
BO,CO,DO 应满足下列的哪个条件( )
(A)AO=CO
(B)BO=DO
(C)AC=BD
(D)AO=CO且BO=DOD3.(威海·中考)在△ABC中,AB>AC,
点D,E分别是边AB,AC的中点,点F在
BC边上,连接DE,DF,EF,则添加下
列哪一个条件后,仍无法判定△BFD
与△EDF全等( )
(A)EF∥AB (B)BF=CF
(C)∠A=∠DFE (D)∠B=∠DEF【解析】选C.因为当EF∥AB时,四边形BDEF是平行四边形,△BFD≌△EDF;当BF=CF时,点F为BC的中点,四边形BDEF是平行四边形,△BFD≌△EDF;当∠B=∠DEF时,因为DE∥BC,∠DEF=∠EFC,所以∠B=∠EFC,EF∥AB, 四边形BDEF是平行四边形,△BFD≌△EDF.(2)运用所学有关知识设计合适可行的方案,并说明理由.(1)应用三角形全等测量距离(构造全等三角形). 通过本课时的学习,需要我们掌握:海到天边天作岸,山登绝顶我为峰.
