【备考2020.难点直击】科学二轮复习 (物理) 简单机械计算
文档属性
| 名称 | 【备考2020.难点直击】科学二轮复习 (物理) 简单机械计算 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2020-04-21 20:43:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【备考2020.难点直击】科学二轮复习 (物理) 简单机械计算
一、杠杆计算
1.如图,将长为1.2米的轻质杆平放在水平方形台面上,杆左右两端点分别为A、B,它们距台面边缘处的距离均为0.3米。在A端挂一个重为30牛的物体,在B端挂一个重为G的物体。问:
(1)若G=30牛,则台面受到杆的压力为多少牛?
(2)若要使杆右端下沉,B端挂的物体至少要大于多少牛?
(3)若B端挂物体后,杆仍在水平台面上静止,则G的取值范围是多少牛?
2.如图所示,轻质杠杆OP长1m,能绕O点转动,P端用细绳悬于N点。现有一质量为1kg的物体A通过滑环挂在M点(滑环和绳子的质量可忽略),OM的长度为0.1m,由于杆OP与水平方向成30°角倾斜,滑环刚好能由M向P端匀速滑动,滑动速度为0.02m/s,细绳能承受的最大拉力为9N。(g取10N/kg)求:
(1)滑环从M点开始滑动,经过多长时间后细绳会断裂;
(2)从滑环自M点滑动到细绳PN断裂时,A所受重力做的功;
(3)上述过程中,A所受重力做功的功率。
3.某科学兴趣小组利用硬棒(质量可忽略不计)、细线、若干已知重力的物体、刻度尺等器材来研究杠杆平衡的条件。如图所示,在C处挂一待测物体B,当重为8牛的物体A挂在D处时,硬棒在水平位置平衡, 用刻度尺测得OC为6厘米,OD为18厘米。
(1)此时物体B的重力是多少牛?
(2)保持O点位置和物体A的重力不变,在C处挂上不同重力的物体,移动物体A的位置,使硬棒在水平位置平衡,分别在OE上标出相应的重力值所对应的刻度,就制成了一根能直接读出待测物体重力的杠杆。问该杠杆的刻度是否均匀?请说明理由。
4.小明利用一根木筷、物体M、托盘和烧杯自制简易密度秤,主要制作步骤如下:
①如图所示,将烧杯放入A端的托盘中,改变物体M悬挂点的位置至B,使木筷在水平位置静止;②在A端的烧杯内注入体积为V的水,改变物体M悬挂点的位置至C,使木筷在水平位置再次静止,在C点标注水的密度值为1.0g/cm3;
③在A端的烧杯内注入体积为V0的其它液体,重复步骤②,在密度秤上标注刻度。
(1)要在该密度秤上标出密度为0.5g/cm3的刻度线,则所标刻度线________?(选填“在”或“不在”)BC的中间位置;
(2)小明发现他所制成的密度秤相邻两刻度线之间的距离太小,导致用此密度秤测量液体密度时误差较大,为此同学们提出了如下改进方案,其中可行的是 ?????:
A.?增大物体M的质量???????????????????????????????B.?换长些的木筷制作密度秤
C.?换更轻的木筷制作密度秤?????????????????????D.?标密度秤的刻度线时,适当增大装入烧杯的液体的体积V0
(3)小明最终所制成的密度秤,OA的长度为4m,OB的长度为2m,OD的长度为10cm,物体M的质量为100g,每次测量时,在A端烧杯内均倒入体积为100cm3的液体,则该密度秤所能测量的液体的最大密度为多少?
5.图甲是一种壶口处配有自动开合小壶盖的电水壶。
(1)如图乙,电水壶底部的导线连接装置有铜环①、铜环②和铜柱③。经测试发现:①、②是绝缘的,②、③之间常温下有十几欧姆的电阻。则与水壶金属外壳相连的装置是________。
(2)图丙是自动开合小壶盖简化侧视图。OA是小壶盖,C是其重力作用点。B是小壶盖的配重。OB是配重柄。AOB能绕固定点O自由转动。请在图丙中作出小壶盖的重力G及其力臂l。
(3)已知:小壶盖质量为4g,OA=3cm,OC=1.4cm,OB=1cm,∠AOB=135°。要求倒水时,壶身最多倾斜45°,小壶盖便自动打开;壶身竖直时,小壶盖在水平位置自动闭合。求配重B的质量取值范围。(配重柄质量和O点的摩擦均忽略不计, 取1.4)
6.如图所示,质量不计的轻板AB可绕转轴O在竖直面内转动,OA=0.4m,OB=1.6m.地面上质量为15kg、横截面积为0.3m2的圆柱体通过绳子与A端相连。现有大小不计、重为50N的物体在水平拉力F=10N的作用下,以速度V=0.2m/s从O点沿板面向右作匀速直线运动。求:?
(1)物体开始运动前,圆柱体对地面的压强;
(2)物体在板面上运动的时间;
(3)物体在板面上运动过程中,拉力F做功的功率
7.将一个圆柱体A分别竖直放在水和液体甲中,都能漂浮,并且分别有2/5和1/4的体积露出液面。
(1)两种情况下,圆柱体A所受浮力之比为________;
(2)甲液体的密度为________;
(3)如图,现有一个左右力臂之比为3:1的轻质杠杆。用细线将圆柱体A悬挂在杠杆左端并放入液体甲中,再用细线在杠杆右端悬挂一个完全相同的圆柱体B并放在水平地面上,当杠杆两端细线均被拉直且平衡时,圆柱体A有1/3的体积露出液面,且该圆柱体底面所受液体压强为800Pa。①请在图中画出地面受圆柱体B压力的示意图;
②求此时圆柱体B对地面的压强为多少?
二、滑轮计算
8.?如图所示,小明用滑轮组将重为500N的物体在10s内匀速提升了1.5m.每个滑轮的重相等,均为20N,不计绳重及摩擦.求:
(1)小明受到地面的摩擦力.
(2)小明做功的功率.
(3)滑轮组的机械效率.
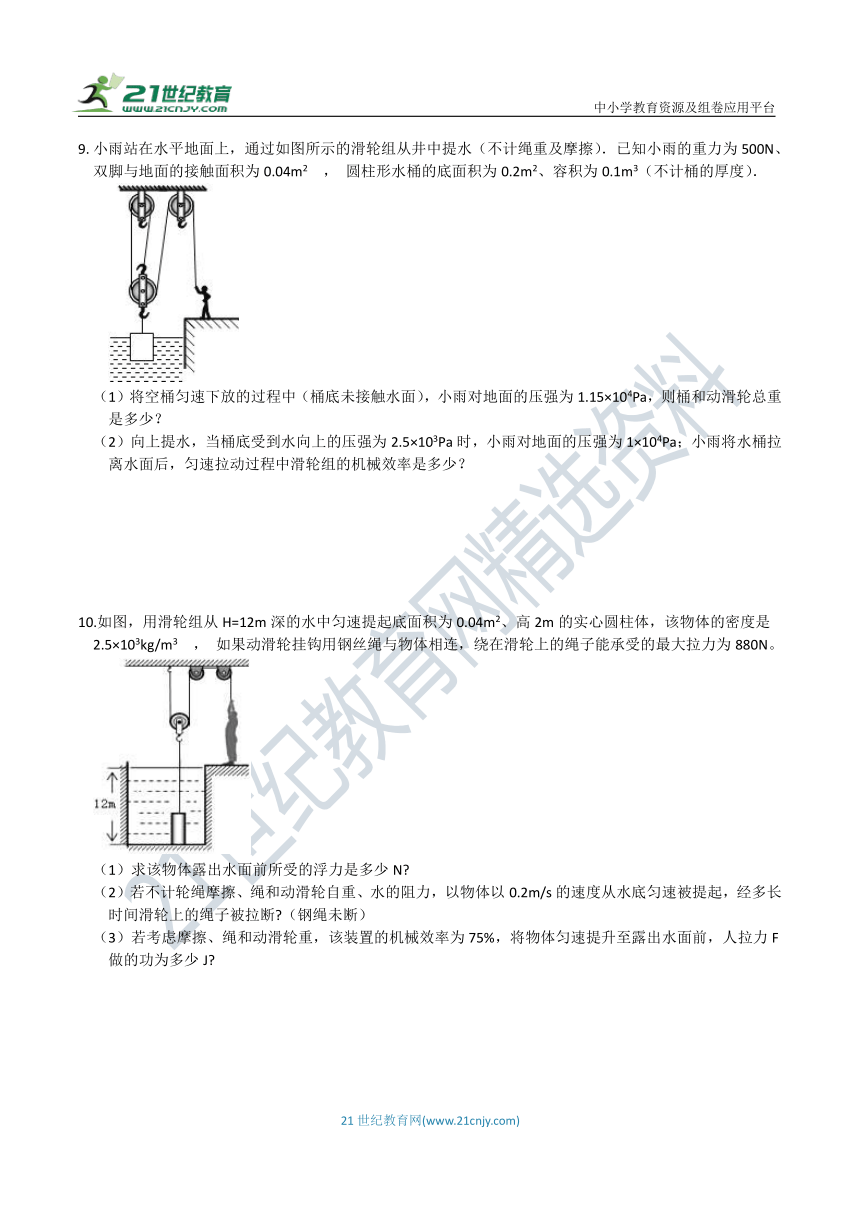
9.?小雨站在水平地面上,通过如图所示的滑轮组从井中提水(不计绳重及摩擦).已知小雨的重力为500N、双脚与地面的接触面积为0.04m2 , 圆柱形水桶的底面积为0.2m2、容积为0.1m3(不计桶的厚度).
(1)将空桶匀速下放的过程中(桶底未接触水面),小雨对地面的压强为1.15×104Pa,则桶和动滑轮总重是多少?
(2)向上提水,当桶底受到水向上的压强为2.5×103Pa时,小雨对地面的压强为1×104Pa;小雨将水桶拉离水面后,匀速拉动过程中滑轮组的机械效率是多少?
10.如图,用滑轮组从H=12m深的水中匀速提起底面积为0.04m2、高2m的实心圆柱体,该物体的密度是2.5×103kg/m3 , 如果动滑轮挂钩用钢丝绳与物体相连,绕在滑轮上的绳子能承受的最大拉力为880N。
(1)求该物体露出水面前所受的浮力是多少N?
(2)若不计轮绳摩擦、绳和动滑轮自重、水的阻力,以物体以0.2m/s的速度从水底匀速被提起,经多长时间滑轮上的绳子被拉断?(钢绳未断)
(3)若考虑摩擦、绳和动滑轮重,该装置的机械效率为75%,将物体匀速提升至露出水面前,人拉力F做的功为多少J?
11.如图是水位装置的示意图。该装置主要由滑轮C、D,物体A、B以及轻质杠杆MN组成。物体A通过细绳与滑轮C相连,物体B通过细绳与杠杆相连。杠杆可以绕支点O在竖直平面内转动,杠杆始终在水平位置平衡,且MO:MN=1:3。物体B受到的重力为100N,A的底面积为0.04m2 , 高1m。当物体A恰好浸没在水中时,物体B对电子秤的压力为F1;若水位下降至物体A恰好完全露出水面时,物体B对电子秤的压力为F2 , 已知:F1﹕F2=6﹕1。滑轮重、滑轮与转轴的摩擦、杠杆与轴的摩擦均忽略不计。求:
(1)物体A完全浸没时,A受到的浮力F浮。________
(2)物体A的密度ρA。________
(3)当物体A有部分浸入水中时,如果把细绳由N端向左移动到N′处,电子秤的示数恰好为零,NN′:MN=1﹕6,此时物体A浸在水中的体积V浸。________
12.?如图所示,是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图.已知井深12m,物体重G=6×103N,汽车重G车=3×104N,汽车匀速拉绳子时的拉力F=2.2×103N,汽车受到的阻力为车重的0.1倍.求:
(1)将物体从井底拉至井口的过程中,汽车拉绳子的拉力对滑轮组做了多少功?
(2)滑轮组的机械效率为多少?(保留一位小数)
(3)若汽车运动的速度为3m/s,则将物体由井底拉至井口需要多长时间?
(4)汽车牵引力为多少?牵引力的功率为多少?
13.新农村建设中,某工人利用如图所示的滑轮组提升重2700N的物体,物体上升了2m,绳子末端的拉力为750N,不计绳重和摩擦力,求:
(1)工人做的有用功是多少?
(2)该滑轮组的机械效率是多少?
(3)动滑轮的总重力是多少N?
14.在拓展课上,小泉同学模拟某建筑工地上拉动工件的情景,设置了如图所示的滑轮组。他用该滑轮组在4秒内将一个重为100牛的物体,沿着水平地面匀速拉动了2米。人的拉力为18牛,物体移动时受到地面的摩擦力为物重的0.35倍,不计绳重及机械的摩擦。求:
(1)人的拉力所做的功。
(2)人的拉力做功的功率。
(3)动滑轮受到的重力。
15.利用如图所示的滑轮组,用F=800N的力拉绳子自由端,货物A重3000N,A以0.6m/s的速度匀速直线运动10s,整个过程中,滑轮组的机械效率为75%,求:
(1)货物A在10s内移动的距离。
(2)该过程中拉力F的功率。
(3)水平地面对货物A的摩擦力大小。
16.如图所示用滑轮组打捞水中物体的示意图,已知物体A的质量为80kg,体积为2×10-2m3。当卷扬机加在绳子自由端竖直向下的拉力F为400N时,物体A在水中以0.1m/s的速度匀速竖直上升(物体A始终未露出水面。不计绳重和摩擦,g取10N/kg)。求:
(1)物体A在水中(未露出水面)时受到的浮力F浮;
(2)物体A在水中匀速竖直上升时,拉力F的功率P;
(3)动滑轮所受的重力G动。
17.如图所示,是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图.已知井深12m,物体重G=6×103N,汽车重G车=3×104N,汽车匀速拉绳子时的拉力F=2.2×103N,汽车受到的阻力为车重的0.1倍.求:
(1)将物体从井底拉至井口的过程中,汽车拉绳子的拉力对滑轮组做了多少功?
(2)滑轮组的机械效率为多少?(保留一位小数)
(3)若汽车运动的速度为3m/s,则将物体由井底拉至井口需要多长时间?
(4)汽车牵引力为多少?牵引力的功率为多少?
18.小明到某山区旅游时,发现一种利用滚轴和绳子组装的特殊机械(如图所示),当地人借助这种装置可以将较重的物体很轻便地搬运到二楼上面,对此小明充满好奇,经主人同意后,小明借助该装置,用很小拉力就能将质量为80千克的重物匀速提升了3米!请根据所学知识解答下列问题:
(1)该装置可简化看成由定滑轮和动滑轮组成的滑轮组,则属于动滑轮是的________.(选填“A”或“B”).
(2)重物上升3米的过程中,小明对重物做的功为多少?
(3)主人介绍滑轮B的质量为5千克,不计绳重和摩擦,整个过程中,小明做的功是多大?
三、斜面和效率计算
19.?小明想把重1000N的木箱A搬到高h=5m,长L=10m的斜面上,如图所示.他站在斜面上,沿斜面向上用F=600N的拉力使木箱A以v=0.2m/s的速度匀速从斜面底端拉到斜面顶端.求:
(1)小明同学拉木箱的功率是多大?
(2)该斜面的机械效率是多少?
(3)木箱A在斜面上匀速运动时受到的摩擦力是多大?
20.?某工人用如图所示的装置把一重为1200N的箱子从斜面底端匀速拉到顶端用时10秒,已知斜面长6m、高2m,此装置的机械效率为80%(滑轮重、绳重、滑轮与绳之间的摩擦均不计).求:
(1)拉力F;
(2)拉力F做功的功率;
(3)箱子和斜面间的摩擦力.
21.在荆州火车站附近的荆州中学新校区的建设工地上,工人把重1 200牛的物体沿着长L=5米、高h=1米的斜面从底部匀速拉上斜面的顶端,沿斜面所用的拉力为300牛(不计空气阻力)。求:
(1)将物体从斜面底部匀速拉到斜面顶端的过程中,拉力做了多少功?
(2)工人使用斜面做功的机械效率是多少?
(3)物体和斜面之间的摩擦力是多大?
22.?如图所示,现将重为5N的物体A沿长1.2m,高0.6m的斜面匀速从底端拉到顶端,在此过程中,F的大小恒为3N,所有时间是12s,求:
(1)物体A从底端到顶端的平均速度
(2)物体A从底端到顶端过程中拉力F的功率
(3)求此斜面的机械效率.(保留一位小数)
23.?建筑工人要向楼上运送货物,为了省力,他在一个斜面上安装了一个滑轮组,做成如图所示的机械装置,斜面的倾角为30°且固定在水平面上.工人用400N的力拉绳子,重为500N的货物沿斜面匀速向上运动6m所用时间为20s,求此过程中
(1)重物沿斜面匀速运动的速度大小
(2)工人提升重物做的有用功
(3)该装置的机械效率
答案解析部分
一、杠杆计算
1.【答案】 (1)解:若 G=30牛,台面受到杆的压力为左右两侧力之和,故为30N+30N=60N
(2)解:根据公式:F1×L1=F2×L2 , 若要使杆右端下沉,则支点在平台右侧,故有:
FA×0.9m=FB×0.3m,因为FA=30N,所以FB??? = =90N
(3)解:根据公式:F1×L1=F2×L2 , 若 B端挂物体后,杆仍在水平台面上静止,即轻质杆既不向右倾斜也不向左倾斜。
不 向 右 倾 斜 时,FA×0.9m=FB×0.3m,即FB = =90N。
不向左倾斜时,FA×0.3m=FB×0.9m,即FB = =10N。
故G的取值范围是:10牛≤G≤90牛(或10~90N)
2.【答案】 (1)解:设经t时间后绳子会断裂,由杠杆平衡条件有:
(2)解:重力做的功
(3)解:重力做功的功率
3.【答案】 (1)解:硬棒在水平位置平衡,有:GB×OC=GA×OD,即:GB×6cm=8N×18cm,所以GB=24N
答:物体B的重力是24N;
(2)解:设待测物体重为G,物A距离O点为L,由杠杆平衡得,G×OC=GA×L,
即L= ,由于 是定值,所以L与G成正比,由此可知刻度均匀的。
答:该杠杆的刻度是均匀的,因为L= ×G( 是定值)。
4.【答案】 (1)在(2)D(3)2×10Kg/m3
5.【答案】 (1)铜环①
(2)
(3)当配重柄水平时,可求出配重的最小质量,杠杆示意图如图2?:
? ? ? ? ? ? ? ?图2
因为∠COB=135°,所以∠DOC=180°-135°=45°;
那么阻力臂OD=sin45°OC=??×OC=??×1.4cm=1cm;
根据杠杆的平衡条件:G1l1=G2l2 ,
m1gl1=m2gl2;
解得:??;
当小壶盖水平时,可求出配重的最大质量,杠杆示意图如图3:
因为∠COB=135°,所以∠BOE=180°-135°=45°;
那么动力臂OE=sin45°OB=??×OB=??×1cm≈0.71cm;
根据杠杆的平衡条件:G1l1′=G2l2′;
m1gl1′=m2gl2′;
那么?;
因此配重B的质量取值范围为4g~7.89g。
6.【答案】 (1)解: 物体开始运动前,圆柱体对地面的压力:
F=G圆柱=m圆柱g=15kg×10N/kg=150N;
圆柱体对地面的压强:;
(2)解:由杠杆的平衡条件可得:G圆柱?OA=G物体?s,
即:150N×0.4m=50N×s;
解得:s=1.2m;
物体在板面上运动的时间:;
(3)解:物体在板面上运动过程中,拉力F做的功:
W=Fs=10N×1.2m=12J,拉力的功率:。
7.【答案】(1)1:1
(2)0.8g/cm3
(3)①如图:
②∵圆柱体A竖直放在水和溶液甲中,都能漂浮,
∴F浮水=F浮甲=G,即:ρ水g(1-2/5)V=ρ甲g(1-1/4)V,
∴ρ甲=4/5ρ水=4/5×1×103kg/m3=0.8×103kg/m3 ,
ρA=3/5ρ水=3/5×1×103kg/m3=0.6×103kg/m3 ,
∵设圆柱体A的高为h,底面积为S,圆柱体A在液体甲中时底面所受压强为800Pa.
∴液体甲对A的压力A受到的浮力
F浮=pS 即ρ甲g(1-1/3)Sh=pS
h= p/[(ρ甲g(2/3)]= 800Pa/(0.8×103kg/m3×10N/kg×2/3)=0.15m
圆柱体A、B、杠杆的受力示意图如图:
则FA=G-F浮 , FB=G-N,
根据杠杆平衡条件得:F1L1=F2L2 , 即FAL1=FBL2
∴(G-F浮)L1=(G-N)L2 , 又∵L1:L2=3:1,∴3(G-F浮)=G-N,∴N=3F浮-2G=3ρ甲g(1-1/3)V-2ρAgV=2gSh(ρ甲-ρA)
所以圆柱体B对地面的压力为:F=N=2gSh(ρ甲-ρA),
压强为:
p=F/S=2gh(ρ甲-ρA)
=2×10N/kg×0.15m×(0.8×103kg/m3-0.6×103kg/m3)=600Pa
二、滑轮计算
8.【答案】(1)?解:以下面动滑轮为研究对象可得,F1的大小:
F1=(G物+G动)=×(500N+20N)=260N,
以上面动滑轮为研究对象,F2的大小:
F2=(F1+G动)=×(260N+20N)=140N,
因小明受向左的绳子拉力F2和地面的摩擦力f而处于静止状态,
所以,f=F2=140N;
(2)以下面动滑轮为研究对象,则F1段绳子运动的距离:
s1=2h=2×1.5m=3m,
以上面动滑轮为研究对象,则F2段绳子运动的距离:
s2=2s1=2×3m=6m,
小明做功的功率:
P====84W;
(3)滑轮组的机械效率:
η=×100%=×100%=×100%≈89.3%.
9.【答案】(1)?解:由p=可得,小雨对地面的压力:
FN=p人S人=1.15×104Pa×0.04m2=460N,
小雨对绳子的拉力:
F=G人﹣FN=500N﹣460N=40N,
由图可知,n=3,不计绳重及摩擦,由F=G可得,桶和动滑轮总重:
G0=nF=3×40N=120N;
(2)由p=ρgh可得,桶底所处的深度:
h1===0.25m,
水桶排开水的体积:
V1=Sh1=0.2m2×0.25m=0.05m3<0.1m3 ,
水桶受到的浮力:
F浮=ρ水gV排=ρ水gV1=1.0×103kg/m3×10N/kg×0.05m3=500N,
此时小雨对地面的压力:
FN′=p人′S人=1×104Pa×0.04m2=400N,
小雨对绳子的拉力:
F′=G人′﹣FN=500N﹣400N=100N,
由F=(G+G0)可得,水的重力:
G水=nF′+F浮﹣G0=3×100N+500N﹣120N=680N,
水桶拉离水面后,匀速拉动过程中滑轮组的机械效率:
η=×100%=×100%=×100%=×100%=85%.
10.【答案】(1)解:V排=V物=0.08m3未出水面前:F浮=ρ水Vg=800N
(2)解:当绳子恰好断时,钢绳拉力为880N×2=1760N而G物=ρ物Vg=2000N
?F浮=2000N-1760N=240N
V排= F浮/ρ水g=0.024m3,h=V/S=0.6m
物体上升11.4m,t=S/V=57s
(3)解:在水下时,有用功为钢绳拉力做功,W有=(G物-F浮)h=(2000N-800N)×10m=12000J
???? W人= W有/η=12000J/75%=16000J
11.【答案】 (1)由阿基米德原理可知:F浮=ρ水gSh=1000kg/m3×10N/kg×0.04m2×1m=400N;答:A受到的浮力为400N
(2)当A恰好完全浸没在水中时,根据杠杆平衡条件得:FM×OM=FN×ON
1/4(GA-F浮)×OM=FN×2OM
FN=1/8(GA-F浮)
物体B对电子秤的压力为:100N–1/8(GA-F浮)
同理,当A恰好完全露出水面时,物体B对电子秤的压力为:100N-1/8GA
[100N–1/8(GA-F浮)]÷[100N-1/8GA]=6
解得:GA=720N;
∴ρA= =720N÷(10N/kg×0.04m2×1m)=1.8×103kg/m3;
答:物体A的密度为1.8×103kg/m3
(3)当把N移到N′处时:1/4(720N-F浮‘)×OM=100N×3/2OM
解得:F浮‘=120N;
∴V排=F浮‘/ρ水g=120N/(1000kg/m3×10N/kg)=0.012m3;
答:物体A浸在水面的体积为0.012m3
12.【答案】(1)解:n=3,s=3h=3×12m=36m,
汽车拉绳子的拉力对滑轮组做的功:
W=Fs=2.2×103N×36m=7.92×104J
答:汽车拉绳子的拉力对滑轮组做了7.92×104J的功
(2)解:滑轮组的机械效率:
?
答:滑轮组的机械效率为90.9%
(3)解:v物=v=×3m/s=1m/s,
由v=得,将物体由井底拉至井口需要的时间:
答:若汽车运动的速度为3m/s,则将物体由井底拉至井口需要12s
(4)解:牵引力:
F牵=F′+f=F′+0.1G车=2.2×103N+0.1×3×104N=5.2×103N,
拉力做功功率:
P===FvP=F牵υ汽=5.2×103N×3 m/s=1.56×104W
答:汽车牵引力为5.2×103N,牵引力的功率为1.56×104W
13.【答案】(1)解:使用滑轮组做的有用功:
W有用=Gh=2700N×2m=5400J
工人做的有用功是=5400J
(2)解:
由图可知,承担物重的绳子股数n=4,则s=4h,
使用滑轮组做的总功:W总=Fs=Fnh=750N×4×2m=6000J,
滑轮组的机械效率:
答:该滑轮组的机械效率是=90%
(3)解:不计绳重和摩擦力,
绳子自由端拉力:
即:,
解得:G动=300N
答:动滑轮的总重力是300N
14.【答案】(1)解:s=2×2米=4米
W=Fs=18牛×4米=72焦
(2)解:
(3)解:f=0.35G=0.35×100牛=35牛
15.【答案】(1)S=Vt=0.6m/s×10s=6m
(2)解:n=3,绳子自由端拉力F的速度为V=0.6m/s×3=1.8m/s
???? P=FV=800N×1.8m/s=1440w
(3)η=W有/W总 , W总=Pt=FS=14400J,W有=14400J×75%=10800J,
有滑轮组水平移动重物过程中,克服重物受到的摩擦力做功为有用功,W有=fS物
??? 故f= W有/S物=10800J/6m=1800N
16.【答案】(1)F浮=ρ水gV排=ρ水gV=1×103kg/m3×10N/kg×2×10-2m3=200N
(2)?拉力端移动的速度v=2vA=2×0.1m/s=0.2m/s
拉力F的功率:P=Fv=400N×0.2m/s=80W
(3)动滑轮的重力为G动 , A完全在水中时绳上拉力为T
GA=F浮+T????
所以T= GA-F浮=800N-200N=600N
所以G动=2F-T=2×400N-600N=200N
17.【答案】(1)解:由图知,n=3,
将物体从井底拉至井口的过程中,绳端移动的距离:s=3h=3×12m=36m,
汽车拉绳子的拉力对滑轮组做的功:
W总=Fs=2.2×103N×36m=7.92×104J
(2)解:W有用=Gh=6×103N×12m=7.2×104J;
滑轮组的机械效率:η= = ×100%≈90.9%
(3)解:已知汽车运动的速度为v=3m/s,
则物体上升速度:v物= v= ×3m/s=1m/s,
由v= 得,将物体由井底拉至井口需要的时间:t物= = =12s
(4)解:汽车匀速运动时,受向右的牵引力、向左的绳子拉力和向左的阻力,
根据力的平衡条件可得牵引力:
F牵=F+f=F+0.1G车=2.2×103N+0.1×3×104N=5.2×103N,
牵引力做功功率:
P=F牵v汽=5.2×103N×3m/s=1.56×104W.
18.【答案】(1)B
(2)解:重物重力:G=mg=80kg×10N/kg=800N,
小明对重物做的功:W有用=Gh=800N×3m=2400J
(3)解:动滑轮B的重力:G轮=m轮g=5kg×10N/kg=50N,
由图知,n=5,
不计绳重和摩擦,拉力:F= (G+G轮)= (800N+50N)=170N,
拉力端移动距离:s=5h=5×3m=15m,
小明做的功:W总=Fs=170N×15m=2550J
三、斜面和效率计算
19.【答案】 (1)因为F=600N,v=0.2m/s,
所以小明同学拉木箱的功率为:P===Fv=600N×0.2m/s=120W;
(2)因为G=1000N,h=5m,
所以做的有用功为:W有用=Gh=1000N×5m=5000J,
做的总功W总=Fs=600N×10m=6000J
则机械效率为:η=×100%=×100%≈83.3%.
(3)额外功为:W额外=W总﹣W有用=6000J﹣5000J=1000J,而W额外=fL,
则摩擦力的大小为:f===100N.
20.【答案】(1)?解:
由图可知滑轮装置是一个动滑轮,
绳端移动的距离:s′=2s=2×6m=12m;
有用功:W有用=Gh=1200N×2m=2400J;
根据η==可得,
所以F===250N.
(2)拉力做的功:W总=Fs′=250N×12m=3000J,
拉力的功率:P===300W;
(3)因为W总=W有用+W额
所以克服摩擦力做的额外功:
W额=W总﹣W有用=3000J﹣2400J=600J,
根据W=fs可得,
摩擦力f===100N.
21.【答案】 (1)解:知道沿斜面的拉力是300牛,斜面的长度是5米,故W总=Fs=F·L=300牛×5米=1 500焦
(2)解:此时W有用=Gh=1 200牛×1米=1 200焦
η= = ×100%=80%
(3)解:W额外=W总-W有用=1 500焦-1 200焦=300焦
根据W额外=fL,得f= = =60牛
22.【答案】(1)物体A从底端到顶端的平均速度:v===0.1m/s.
(2)拉力做的总功W总=Fs=3N×1.2m=3.6J,
则拉力的功率P===0.3W.
(3)拉力做的有用功W有=Gh=5N×0.6m=3J,
则此斜面的机械效率η=×100%=×100%≈83.3%.
23.【答案】(1)解:物体移动距离s=6m,运动时间t=20s,货物运动速度v===0.3m/s
答:重物沿斜面匀速运动的速度为0.3m/s
(2)解:斜面的倾角为30°,根据直角三角形特点,物体在斜面移动6m,上升的高度h=s=×6m=3m,
工人所做有用功:W有用=Gh=500N×3m=1500J
答:工人提升重物做的有用功是1500J
(3)解:由图可知,滑轮组的n值为2,绳子自由端移动距离s′=nh=2×6m=12m,
工人所做总功:W总=Fs′=400N×12m=4800J,
答:该装置的机械效率31.25%
21世纪教育网(www.21cnjy.com)
