【备战2020】中考数学二轮专题 圆中的函数关系问题复习学案(上海地区专用)
文档属性
| 名称 | 【备战2020】中考数学二轮专题 圆中的函数关系问题复习学案(上海地区专用) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
备战2020中考数学二轮专题复习学案
圆中的函数关系问题
【备注】该部分引导学生复习圆的基本性质和垂径定理,大概5分钟左右。
圆心角、弧、弦、弦心距之间的关系:
在同圆或等圆中,圆心角、弧、弦、弦心距四组量中,只要有一组量相等则其余三组量也相等,简称“买一送三”。
垂径定理:
垂径定理是圆与直线的位置关系中最重要的一个定理。如果说对于定理及推论理解实在有难度的话可以从其共性着手。可以这么理解,针对半径而言,“平分圆心角”、“平分弧”、“平分弦”、“垂直弦”四个特点“买一送三”。从推导过程理解垂径定理本质上就是将曾经掌握的等腰三角形“三线合一”置入圆内。因此题型中等腰三角形的性质对于解题过程的帮助明显要突出许多。在应用这一定理的过程中要注意“弦长”“半径”“弦心距”之间存在的关系往往都和勾股定理有关。勾股数的熟练掌握对于此类题型帮助很大。近年来的圆出题方向多偏向于这一定理,压轴题型如果涉及到圆多和垂径定理脱不了干系。故此定理是为圆一章内容的重中之重。
思路一:抓住圆内存在的等腰三角形,利用勾股定理迅速确定可能出现的与题目有关的数据。
思路二:圆内出现“平分”,“垂直”等字眼时本题和垂直定理一般就会产生联系,无论是证明还是求值都必须先掌握住定理提供的其他的几个确定关系。
注意:添加辅助线的技巧,就是将题目中的图形和上图对比,确什么补什么,大部分题目可以解决,但一定要利用好题目中的特殊条件。
【备注】:
以下每题教法建议,请老师根据学生实际情况参考;
在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;
可以根据各题的“参考教法”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;
例题讲解,可以根据“参考教法”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;
引导的技巧:直接提醒,问题式引导,类比式引导等等;
部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;
每个题目的讲解时间根据实际情况处理,建议每题8-10分钟。
三、典型例题
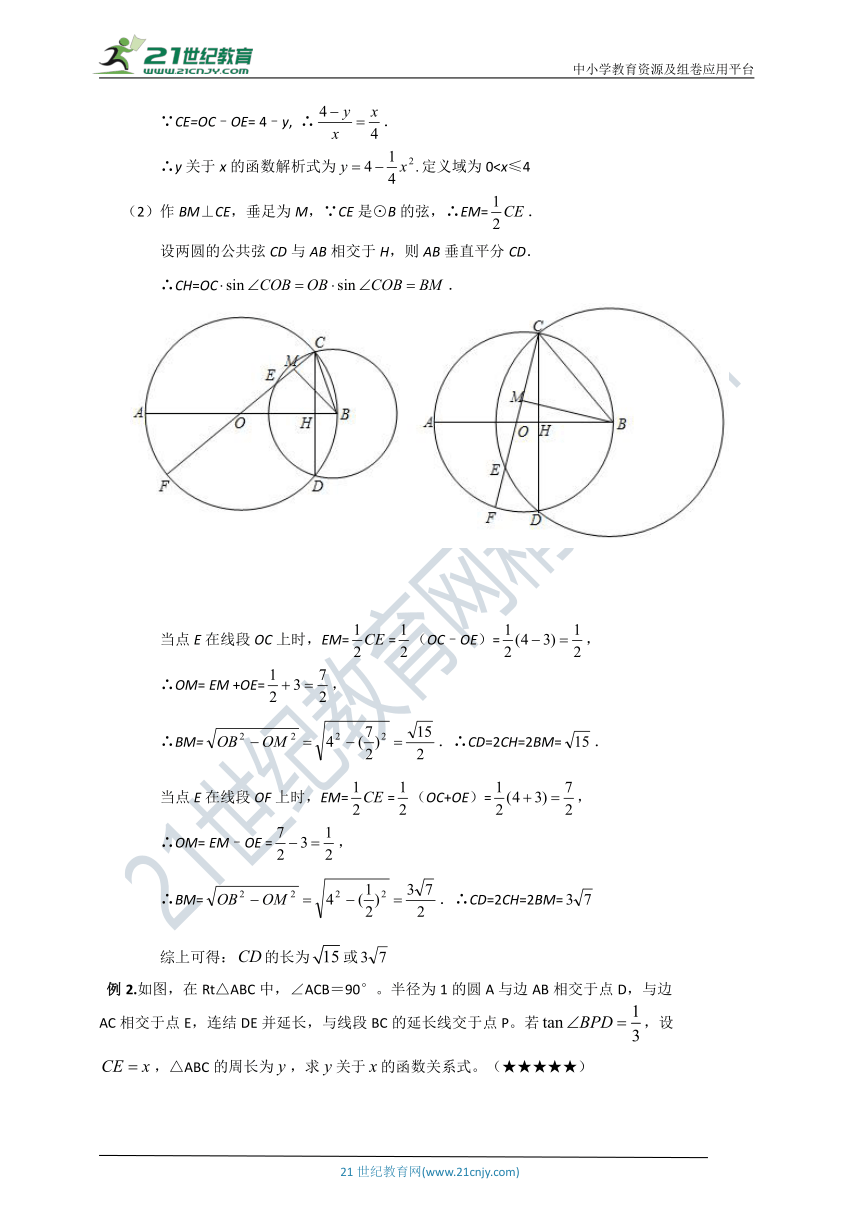
例1.已知:⊙O的直径AB=8,⊙B与⊙O相交于点C、D,⊙O的直径CF与⊙B相交于点E,设⊙B的半径为,OE的长为。(★★★★★)
如图,当点E在线段OC上时,求关于的函数解析式,并写出定义域;
当点E在直径CF上时,如果OE的长为3,求公共弦CD的长。
【参考教法】可参考以下教法引导学生分析问题、解决问题
寻找题目中的已知量和特殊条件:
1.题目中那些边的长度已知?哪些边存在特殊关系? 提示:AB=8
2.找找圆心的位置和半径的大小。提示:⊙O圆心确定、半径为4;⊙B圆心确定、半径为。
求解函数关系式:
1.寻找一下和分别表示什么? 提示:。
2.圆中求解弦长关于半径的函数关系式,一般情况下怎么求解? 提示:过圆心画弦的垂线,用“勾股定理”或“锐角三角比”求解。(另:本题也可以连结用相似求解)
3.添加辅助线,计算求解。
4.注意求解函数定义域。
三.当时,求公共弦的长:
1.点的位置有什么特点? 提示:点E在直径CF上
2.根据题目中点E的位置求解看看。提示:分点在边上和点在延长线上两个情况讨论,注意寻找全等三角形。
【满分解答】
(1)联结BE,∵⊙O的直径AB=8,∴OC=OB=AB=4.∵BC=BE,
∴∠BEC=∠C=∠CBO.∴△BCE∽△OCB.∴.
∵CE=OC–OE= 4–y, ∴.
∴y关于x的函数解析式为定义域为0
设两圆的公共弦CD与AB相交于H,则AB垂直平分CD.
∴CH=OC.
当点E在线段OC上时,EM==(OC–OE)=,
∴OM= EM +OE=,
∴BM=.∴CD=2CH=2BM=.
当点E在线段OF上时,EM==(OC+OE)=,
∴OM= EM–OE =,
∴BM=.∴CD=2CH=2BM=
综上可得:的长为或
例2.如图,在Rt△ABC中,∠ACB=90°。半径为1的圆A与边AB相交于点D,与边
AC相交于点E,连结DE并延长,与线段BC的延长线交于点P。若,设
,△ABC的周长为,求关于的函数关系式。(★★★★★)
[来源:学*科*网]
【参考教法】可以参考以下教法引导学生分析问题、解决问题
寻找题目中的已知量和特殊条件:
1.题中哪些边已知?哪些边存在特殊关系? 提示:,
2.角度关系。 提示:
3.圆心的位置和半径的大小。圆心为定点,半径为1 。
求解函数关系式:
1.寻找一下和分别表示什么? 提示:,△ABC的周长为。
2.怎么求解? 提示:添加辅助线,构造相似基本图形求解
3.怎么计算? 过点作平行线,用“勾股定理”结合“相似三角形”求解。
4.注意求解定义域。
【满分解答】
过D点作DQ⊥AC于点Q,则△DQE与△PCE相似,设AQ=a,则QE=1-a
∴且
∴
∵在Rt△ADQ中,据勾股定理得:
即:,解之得
∵△ADQ与△ABC相似
∴
∴
∴三角形ABC的周长
即:,其中x>0
【备注】:本部分对前面例题中讲到的解题方法进行归类总结,以引导式总结出,建议时间4分钟左右。
四、规律总结
圆中的函数关系问题的解题方法和策略:
1.寻找一下和分别表示什么;
2.观察和是否存在直接关系;
3.寻找相似基本图形和特殊图形,找比例关系式;
4.用“比例关系”或“勾股定理”建立关系式;
5.添加辅助线的策略是:过圆心画弦的垂线,用好垂径定理;
6.注意求解定义域。
五、实战演练:
【备注】该部分需要学生在10分钟内独立完成,满分10分,之后再评分并讲评
1.如图,已知线段AB=10,点C在线段AB上,⊙A、⊙B的半径分别为AC、BC,D是⊙B上一点,AD交⊙A于E,EC的延长线交⊙B于F。(★★★★)(10分)
求证:BF//AD;
若BD⊥AD,AC=,DF=,求与的函数关系式,写出定义域。
【解法点拨】可参考以下方法解答本题
寻找题目中的已知量和特殊条件:
1边:AB=10,BD⊥AD,同一圆中半径相等
2.角:从图中寻找,有很多
3.圆心的位置和半径的大小:
①⊙A的圆心为定点,半径为
②⊙B的圆心为定点,半径为
求解⊙P的半径的半径,过点作垂线,用三角比即可求解。
求解函数关系式:
1.寻找和分别表示什么:AC=,DF=
2.求解:结合“BF//AD+BD⊥AD”得为等腰直角三角形,用勾股定理即可求解。
【满分解答】
证明:(1)∵E、C在⊙A上,F、C在⊙B上,
∴AE=AC,BC=BF................................................................1分
∴∠AEC=∠ACE,∠BCF=∠BFC................................................................1分
∵∠ACE=∠BCF ∴∠AEC=∠BFC................................................................1分
∴BF//AD...................................................................1分
(2)∵BD⊥AD ,BF//AD
∴∠ADB=∠DBF=90°................................................................1分
∵AB=10,AC= ∴BO=10-.........................................................1分
∴BD= BF = BO=10- ∵DF=
∴.........................................................1分
∴.....................................2分+.1分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
