沪科版七年级数学下册第9章:分式 单元复习课件 (共33张PPT)
文档属性
| 名称 | 沪科版七年级数学下册第9章:分式 单元复习课件 (共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 402.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 21:24:15 | ||
图片预览











文档简介
(共33张PPT)
第9章 分式
复习与小结
知识结构图
分式
分式的性质
应用
解法
约分
加减法
分式的运算
分式方程
乘除法
通分
知识点归纳
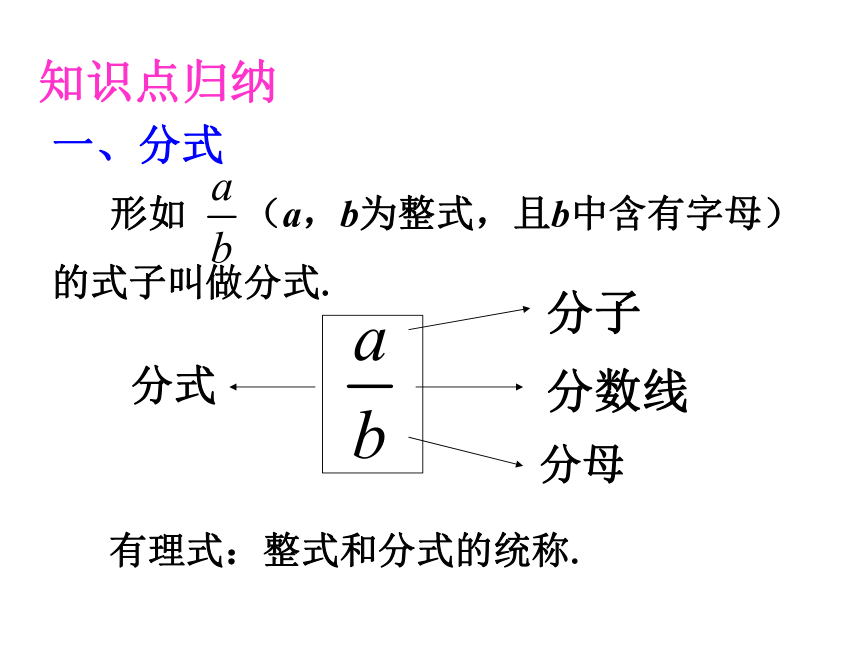
一、分式
形如 (a,b为整式,且b中含有字母)
的式子叫做分式.
有理式:整式和分式的统称.
分子
分母
分数线
分式
分式 有意义的条件:
分母不为0,即b≠0
分式 无意义的条件:
分母为0,即b=0
分式 为0的条件:
分子为0且分母不为0,
即a=0且b≠0
对点练习1
(1)下列各式中分式有_____,整式有_____.
(2)若分式 的值为0,
则x的值为( )
A.1 B.﹣1 C.±1 D.1或0
②④
①③
A
二、分式的性质
约分:把分式的分子与分母的公因式约去
最简分式:分子与分母只有公因式1的分式
通分:化异分母分式为同分母分式的过程
(a、b是整式,m≠0)
对点练习2
对分式 的变形,
甲同学的做法是:
乙同学的做法是:
请根据分式的基本性质,判断甲、乙两位同学的解法是否正确,并说明理由.
解 :甲的解法正确,乙的解法错误,
理由如下:
∵分式 已隐含了a+b≠0的条件,
∴可用分式的基本性质,将分式的分子与分母约去a+b;
而a-b是否为0不确定,
∴不能用分式的基本性质将分式的分子与分母都乘以a-b.
三、分式的运算
乘除:
加减:
混合:先乘方,再乘除,后加减;如果有括
号,先进行括号里的运算.
对点练习3
计算:1.
解:原式=
=
=
2.
解:原式=
=
=﹣2
四、分式方程
概念:分母中含有未知数的方程
与整式方程的区别:分母中是否含有未知数
解法:①去分母,转化为整式方程
②解这个整式方程
③验根
注意:增根的产生
对点练习4
解方程:
解:去分母,得
2(x-1)+3(x+1)=6,
解这个整式方程,得 x=1.
检验:当x=1时,x2-1=0,
∴x=1是原方程的增根,应舍去,
∴原方程无解.
学习方法总结
1.采用类比法学习本章内容,将分式的概念、性质及运算与分数的相关知识类比学习,同时要注意与分数相关内容的区别.
2.要通过课上与课下的巩固练习熟练掌握分式的四则混合运算.
3.学习解分式方程时可与解一元一次方程的内容对比学习,理解它们之间的联系与区别,特别要注意对增根的理解以及验根步骤的书写.
易错题辨析
1.已知分式 的值为0,
则x的值为( )
A.1 B.﹣1 C. ±1 D.x≠1
错解:C
正解:B
辨析:造成错解的主要原因是没有考虑分式有意义的条件——分母不为0,分式的值为0的条件是分子为0且分母不为0.
2.方程 的解是_______.
错解:x=1
正解:无解
辨析:本题错解的主要原因是没有验根,∵解分式方程在去分母时,方程两边同时乘以的式子可能为0,∴解分式方程时必须验根.
典例讲解
例1 先化简: ,
再任选一个你喜欢的数x代入求值.
思考:(1)题中有哪些运算?
(2)应按怎样的顺序计算?
(3)x应满足什么条件?
减法、除法,小括号
先算小括号里面的减法,再算除法
x≠1、2
解:原式=
=
=x﹣2
∵x-1≠0,x-2≠0,∴x≠1、2
∴任选一值,当x=0时,原式=﹣2.
注意x应满足的条件
解题方法归纳
分式的混合运算应注意以下几点:
1.分式运算的根本依据是分式的基本性质,应熟练掌握;
2.要掌握每种运算的法则,不要弄错了法则;
3.一定要分清题中有哪些运算,再按混合运算顺序计算;
4.在求值时要找出题中隐含的条件,如分母不为0,除数不为0等.
例2 端午节期间,我校食堂应教职工的要求,用700元钱购进甲、乙两种粽子共260个,其中甲种粽子比乙种粽子少用100元,且已知甲种粽子单价比乙种粽子单价高20%.求甲、乙种粽子的单价各是多少?两种粽子各购买了多少个?
等量关系:
甲种粽子单价=乙种粽子单价×(1+20%)
甲种粽子个数+乙种粽子个数=260
解:设乙种粽子x个,由题意,得
化为整式方程,得
260×1.2x=300+400×1.2
解得 x=2.5.
经检验,x=2.5是原方程的解且符合题意.
∴(1+20%)x=1.2×2.5=3(元)
当x=2.5时,
乙种粽子个数:400÷2.5=160(个)
甲种粽子个数:260-160=100(个).
答:甲种粽子单价为每个3元,乙种粽子单价为每个2.5元,甲种粽子购买100个,乙种粽子购买160个.
解题方法总结
列分式方程解应用题的一般步骤有哪些?
1.审题:分清已知量与未知量;
2,设未知数;
3.找出等量关系,列出方程;
4.解这个分式方程;
5.验根:是否为原方程的解与是否符合题意;
6.写答语.
1.某施工队挖掘一条长90米的隧道,开工后每天比原计划多挖1米,结果提前3天完成任务,原计划每天挖多少米?若设原计划每天挖x米,则依题意列出正确的方程为( )
A.
B.
C.
D.
D
动笔练一练
2. 某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的 倍,购进数量比第一次少了30支.求第一次每支铅笔的进价是多少元?
解:设第一次每支铅笔进价为x元,由题意列方程,得
解得 x=4.
经检验,故x=4原分式方程的解.
答:第一次每支铅笔的进价为4元.
动笔练一练
1.计算:
原式=2
原式=
原式=a-1
课堂练习
2.解方程:
x=2
无解
3.一艘轮船从甲地逆流航行至乙地,然后从
乙地回到甲地.已知水流速度是3km/h,回来
时所需的时间是去时的 ,求轮船在静水中
的速度.
解:设轮船在静水中的速度为xkm/h,
轮船从甲地到乙地的航程为ykm,
由题意,得
解得 x=21.
经检验,x=21是原方程的解且符合题意.
答:轮船在静水中的速度是21km/h.
能力拓展
一、先化简,再求值:
其中x是方程
的解.
解:化简得,原式=
=
解方程 得x=﹣3,
∴当x=﹣3时,原式= =2.
[点评] 方程的增根就是使方程的最简公分母为零的未知数的值.已知分式方程的增根求未知字母的值时,应该先把分式方程去分母化为整式方程,然后把增根代入这个整式方程求解.
分式
分式
分式的定义及有意义的条件等
分式方程
分式方程的应用
步骤
一审二设三列四解五检六写,尤其不要忘了验根
类型
行程问题、工程问题、销售问题等
分式的运算及化简求值
分式方程的定义
分式方程的解法
课堂小结
第9章 分式
复习与小结
知识结构图
分式
分式的性质
应用
解法
约分
加减法
分式的运算
分式方程
乘除法
通分
知识点归纳
一、分式
形如 (a,b为整式,且b中含有字母)
的式子叫做分式.
有理式:整式和分式的统称.
分子
分母
分数线
分式
分式 有意义的条件:
分母不为0,即b≠0
分式 无意义的条件:
分母为0,即b=0
分式 为0的条件:
分子为0且分母不为0,
即a=0且b≠0
对点练习1
(1)下列各式中分式有_____,整式有_____.
(2)若分式 的值为0,
则x的值为( )
A.1 B.﹣1 C.±1 D.1或0
②④
①③
A
二、分式的性质
约分:把分式的分子与分母的公因式约去
最简分式:分子与分母只有公因式1的分式
通分:化异分母分式为同分母分式的过程
(a、b是整式,m≠0)
对点练习2
对分式 的变形,
甲同学的做法是:
乙同学的做法是:
请根据分式的基本性质,判断甲、乙两位同学的解法是否正确,并说明理由.
解 :甲的解法正确,乙的解法错误,
理由如下:
∵分式 已隐含了a+b≠0的条件,
∴可用分式的基本性质,将分式的分子与分母约去a+b;
而a-b是否为0不确定,
∴不能用分式的基本性质将分式的分子与分母都乘以a-b.
三、分式的运算
乘除:
加减:
混合:先乘方,再乘除,后加减;如果有括
号,先进行括号里的运算.
对点练习3
计算:1.
解:原式=
=
=
2.
解:原式=
=
=﹣2
四、分式方程
概念:分母中含有未知数的方程
与整式方程的区别:分母中是否含有未知数
解法:①去分母,转化为整式方程
②解这个整式方程
③验根
注意:增根的产生
对点练习4
解方程:
解:去分母,得
2(x-1)+3(x+1)=6,
解这个整式方程,得 x=1.
检验:当x=1时,x2-1=0,
∴x=1是原方程的增根,应舍去,
∴原方程无解.
学习方法总结
1.采用类比法学习本章内容,将分式的概念、性质及运算与分数的相关知识类比学习,同时要注意与分数相关内容的区别.
2.要通过课上与课下的巩固练习熟练掌握分式的四则混合运算.
3.学习解分式方程时可与解一元一次方程的内容对比学习,理解它们之间的联系与区别,特别要注意对增根的理解以及验根步骤的书写.
易错题辨析
1.已知分式 的值为0,
则x的值为( )
A.1 B.﹣1 C. ±1 D.x≠1
错解:C
正解:B
辨析:造成错解的主要原因是没有考虑分式有意义的条件——分母不为0,分式的值为0的条件是分子为0且分母不为0.
2.方程 的解是_______.
错解:x=1
正解:无解
辨析:本题错解的主要原因是没有验根,∵解分式方程在去分母时,方程两边同时乘以的式子可能为0,∴解分式方程时必须验根.
典例讲解
例1 先化简: ,
再任选一个你喜欢的数x代入求值.
思考:(1)题中有哪些运算?
(2)应按怎样的顺序计算?
(3)x应满足什么条件?
减法、除法,小括号
先算小括号里面的减法,再算除法
x≠1、2
解:原式=
=
=x﹣2
∵x-1≠0,x-2≠0,∴x≠1、2
∴任选一值,当x=0时,原式=﹣2.
注意x应满足的条件
解题方法归纳
分式的混合运算应注意以下几点:
1.分式运算的根本依据是分式的基本性质,应熟练掌握;
2.要掌握每种运算的法则,不要弄错了法则;
3.一定要分清题中有哪些运算,再按混合运算顺序计算;
4.在求值时要找出题中隐含的条件,如分母不为0,除数不为0等.
例2 端午节期间,我校食堂应教职工的要求,用700元钱购进甲、乙两种粽子共260个,其中甲种粽子比乙种粽子少用100元,且已知甲种粽子单价比乙种粽子单价高20%.求甲、乙种粽子的单价各是多少?两种粽子各购买了多少个?
等量关系:
甲种粽子单价=乙种粽子单价×(1+20%)
甲种粽子个数+乙种粽子个数=260
解:设乙种粽子x个,由题意,得
化为整式方程,得
260×1.2x=300+400×1.2
解得 x=2.5.
经检验,x=2.5是原方程的解且符合题意.
∴(1+20%)x=1.2×2.5=3(元)
当x=2.5时,
乙种粽子个数:400÷2.5=160(个)
甲种粽子个数:260-160=100(个).
答:甲种粽子单价为每个3元,乙种粽子单价为每个2.5元,甲种粽子购买100个,乙种粽子购买160个.
解题方法总结
列分式方程解应用题的一般步骤有哪些?
1.审题:分清已知量与未知量;
2,设未知数;
3.找出等量关系,列出方程;
4.解这个分式方程;
5.验根:是否为原方程的解与是否符合题意;
6.写答语.
1.某施工队挖掘一条长90米的隧道,开工后每天比原计划多挖1米,结果提前3天完成任务,原计划每天挖多少米?若设原计划每天挖x米,则依题意列出正确的方程为( )
A.
B.
C.
D.
D
动笔练一练
2. 某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的 倍,购进数量比第一次少了30支.求第一次每支铅笔的进价是多少元?
解:设第一次每支铅笔进价为x元,由题意列方程,得
解得 x=4.
经检验,故x=4原分式方程的解.
答:第一次每支铅笔的进价为4元.
动笔练一练
1.计算:
原式=2
原式=
原式=a-1
课堂练习
2.解方程:
x=2
无解
3.一艘轮船从甲地逆流航行至乙地,然后从
乙地回到甲地.已知水流速度是3km/h,回来
时所需的时间是去时的 ,求轮船在静水中
的速度.
解:设轮船在静水中的速度为xkm/h,
轮船从甲地到乙地的航程为ykm,
由题意,得
解得 x=21.
经检验,x=21是原方程的解且符合题意.
答:轮船在静水中的速度是21km/h.
能力拓展
一、先化简,再求值:
其中x是方程
的解.
解:化简得,原式=
=
解方程 得x=﹣3,
∴当x=﹣3时,原式= =2.
[点评] 方程的增根就是使方程的最简公分母为零的未知数的值.已知分式方程的增根求未知字母的值时,应该先把分式方程去分母化为整式方程,然后把增根代入这个整式方程求解.
分式
分式
分式的定义及有意义的条件等
分式方程
分式方程的应用
步骤
一审二设三列四解五检六写,尤其不要忘了验根
类型
行程问题、工程问题、销售问题等
分式的运算及化简求值
分式方程的定义
分式方程的解法
课堂小结
