人教版九年级数学下册28.2.2: 第2课时 利用仰俯角解直角三角形课件(共19张PPT)
文档属性
| 名称 | 人教版九年级数学下册28.2.2: 第2课时 利用仰俯角解直角三角形课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 451.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 20:48:55 | ||
图片预览





文档简介
课件19张PPT。 第2课时
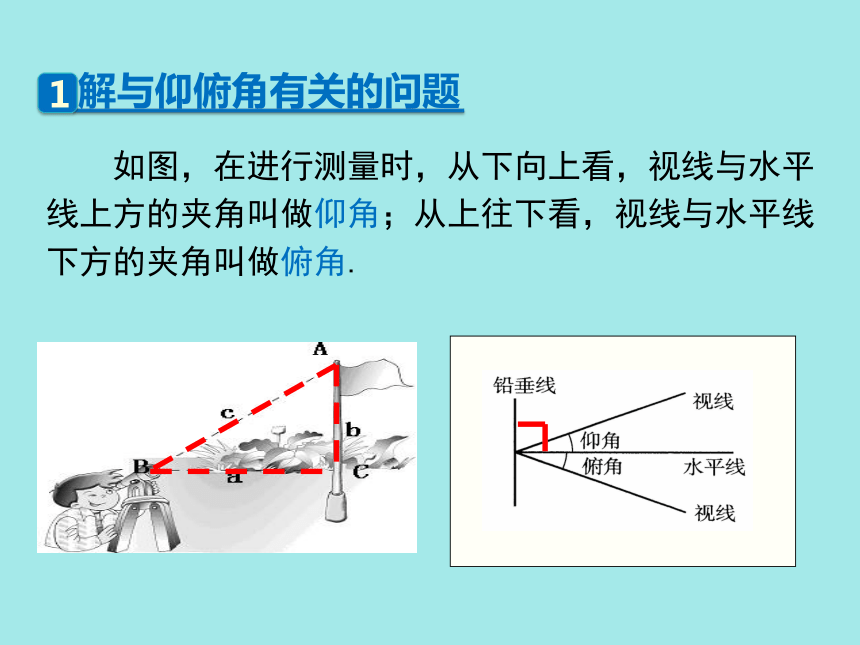
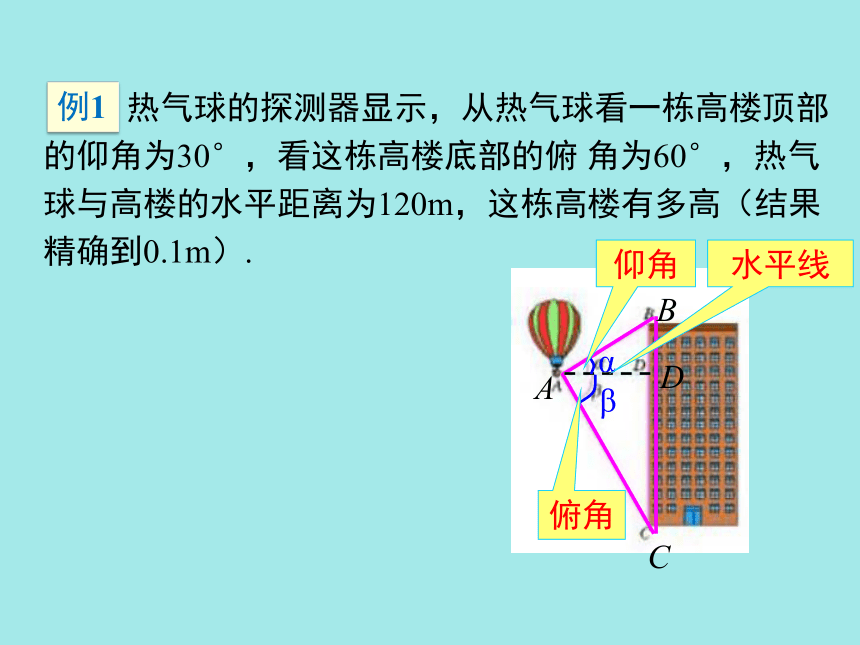
利用仰俯角解直角三角形解与仰俯角有关的问题 如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角. 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).仰角水平线俯角例1分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°.Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度.
解:如图,a = 30°,β= 60°, AD=120.答:这栋楼高约为277.1m.建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).解:在等腰Rt△BCD中, ∠ACD=90°,BC=DC=40m.∴AB=AC-BC=55.2-40=15.2 (m). 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?例2解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°,
D′C′=50m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,设
AB′=x m.如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,
cos37 °≈0.6,tan 37°≈0.75)
AB37°45°400米PABO37°45°400米P设PO=x米,在Rt△POB中,∠PBO=45°,在Rt△POA中,∠PAB=37°,OB=PO= x米.解得x=1200.解:作PO⊥AB交AB的延长线于O.故飞机的高度为1200米.1. 如图1,在高出海平面100米的悬崖顶A处,观测海平
面上一艘小船B,并测得它的俯角为45°,则船与观
测者之间的水平距离BC=_________米.
2. 如图2,两建筑物AB和CD的水平距离为30米,从A点
测得 D点的俯角为30°,测得C点的俯角为60°,则
建筑物CD的高为_____米.1003. 为测量松树AB的高度,一个人站在距松树15米的E
处,测得仰角∠ACD=52°,已知人的高度是1.72米,
则树高 (精确到0.1米). 20.9 米4. 如图,在电线杆上离地面高度5m的C点处引两根拉
线固定电线杆,一根拉线AC和地面成60°角,另一
根拉线BC和地面成45°角.则两根拉线的总长度为
m(结果用带根号的数的形式表示). 5. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
解:由题意,AC=AB=610(米).
(2) 求大楼的高度CD(精确到1米).故BE=DEtan39°.
∵CD=AE,
∴CD=AB-DE·tan39°
=610-610×tan39°≈116(米).解:DE=AC=610(米),
在Rt△BDE中,tan∠BDE= .45°30°BA200米6. 如图,直升飞机在高为200米的大楼AB上方P点处,
从大楼的顶部和底部测得飞机的仰角为30°和45°,
求飞机的高度PO .UDP利用仰俯角解直角三角形仰角、俯角的概念运用解直角三角形解决仰角、俯角问题小结模型一模型三仰角、俯角问题的常见基本模型:
利用仰俯角解直角三角形解与仰俯角有关的问题 如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角. 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).仰角水平线俯角例1分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°.Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度.
解:如图,a = 30°,β= 60°, AD=120.答:这栋楼高约为277.1m.建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).解:在等腰Rt△BCD中, ∠ACD=90°,BC=DC=40m.∴AB=AC-BC=55.2-40=15.2 (m). 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?例2解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°,
D′C′=50m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,设
AB′=x m.如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,
cos37 °≈0.6,tan 37°≈0.75)
AB37°45°400米PABO37°45°400米P设PO=x米,在Rt△POB中,∠PBO=45°,在Rt△POA中,∠PAB=37°,OB=PO= x米.解得x=1200.解:作PO⊥AB交AB的延长线于O.故飞机的高度为1200米.1. 如图1,在高出海平面100米的悬崖顶A处,观测海平
面上一艘小船B,并测得它的俯角为45°,则船与观
测者之间的水平距离BC=_________米.
2. 如图2,两建筑物AB和CD的水平距离为30米,从A点
测得 D点的俯角为30°,测得C点的俯角为60°,则
建筑物CD的高为_____米.1003. 为测量松树AB的高度,一个人站在距松树15米的E
处,测得仰角∠ACD=52°,已知人的高度是1.72米,
则树高 (精确到0.1米). 20.9 米4. 如图,在电线杆上离地面高度5m的C点处引两根拉
线固定电线杆,一根拉线AC和地面成60°角,另一
根拉线BC和地面成45°角.则两根拉线的总长度为
m(结果用带根号的数的形式表示). 5. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
解:由题意,AC=AB=610(米).
(2) 求大楼的高度CD(精确到1米).故BE=DEtan39°.
∵CD=AE,
∴CD=AB-DE·tan39°
=610-610×tan39°≈116(米).解:DE=AC=610(米),
在Rt△BDE中,tan∠BDE= .45°30°BA200米6. 如图,直升飞机在高为200米的大楼AB上方P点处,
从大楼的顶部和底部测得飞机的仰角为30°和45°,
求飞机的高度PO .UDP利用仰俯角解直角三角形仰角、俯角的概念运用解直角三角形解决仰角、俯角问题小结模型一模型三仰角、俯角问题的常见基本模型:
