人教版八年级数学下册:18.2.1 矩形的判定 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册:18.2.1 矩形的判定 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 133.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 00:00:00 | ||
图片预览

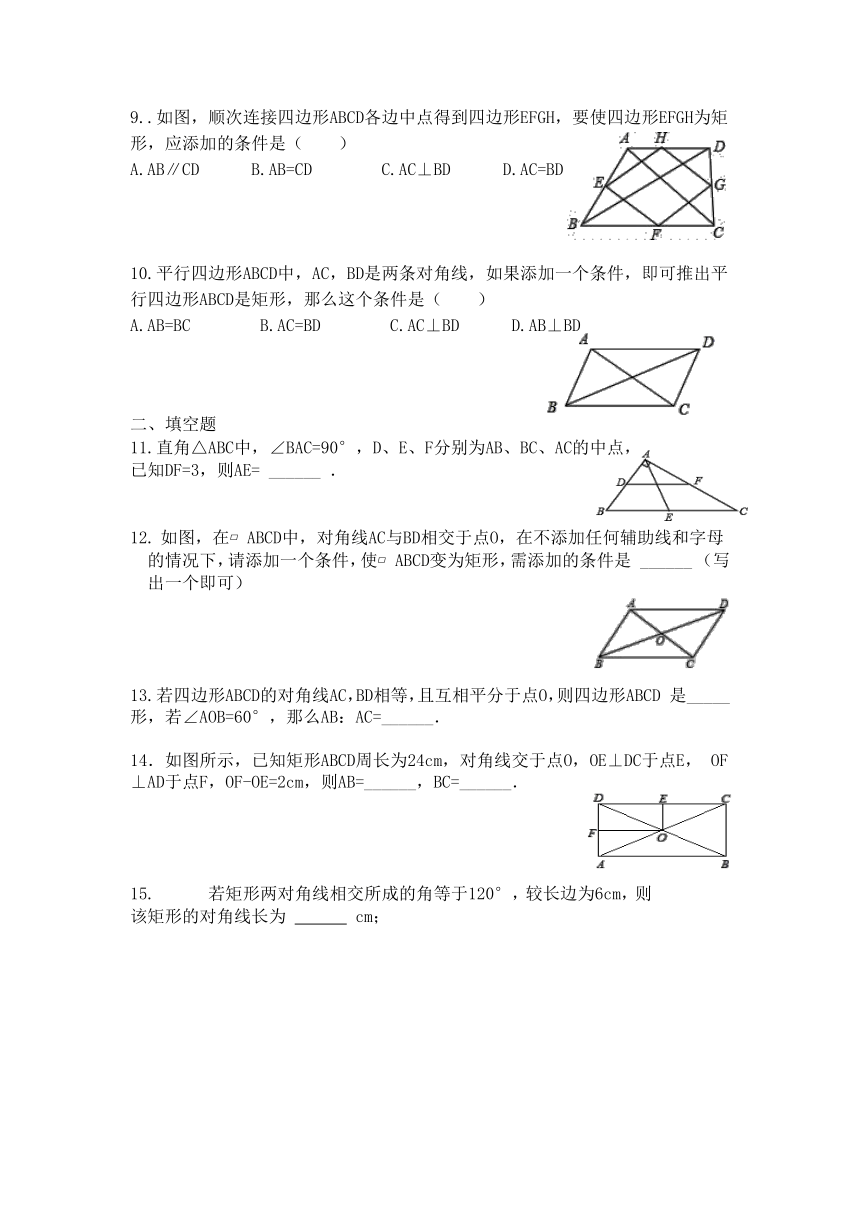

文档简介
18.2 特殊的平行四边形
矩形的判定
选择题
1.下列命题是真命题的是( );
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形
D.对角线互相垂直的四边形是矩形
2.若矩形两邻边的长度之比为2︰3,面积为54cm2, 则其周长( ).
A. 15cm B. 30cm C. 45cm D. 90cm
3.下列叙述中能判定四边形是矩形的个数是( )
①对角线互相平分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线互相平分且相等的四边形.
A.1 B.2 C.3 D.4
4.如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
A. B.4 C. 2 D.
5.下列识别图形不正确的是( )
A.有一个角是直角的平行四边形是矩形
B.有三个角是直角的四边形是矩形
C.对角线相等的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
6.四边形ABCD的对角线相交于点O,下列条件不能判定它是矩形的是( )
A.AB=CD,AB∥CD,∠BAD=90°
B.AO=CO,BO=DO,AC=BD
C.∠BAD=∠ABC=90°,∠BCD+∠ADC=180°
D.∠BAD=∠BCD,∠ABC=∠ADC=90°
7.矩形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相垂直
8.两条平行线被第三条直线所截,两组内错角的平分线相交所成的四边形是( )
A. 一般平行四边形 B. 菱形
C. 矩形 D. 正方形
9..如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥CD???B.AB=CD????C.AC⊥BD???D.AC=BD
10.平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC????B.AC=BD????C.AC⊥BD???D.AB⊥BD
填空题
11.直角△ABC中,∠BAC=90°,D、E、F分别为AB、BC、AC的中点,
已知DF=3,则AE= ______ .
如图,在?ABCD中,对角线AC与BD相交于点O,在不添加任何辅助线和字母的情况下,请添加一个条件,使?ABCD变为矩形,需添加的条件是 ______ (写出一个即可)
13.若四边形ABCD的对角线AC,BD相等,且互相平分于点O,则四边形ABCD是_____形,若∠AOB=60°,那么AB:AC=______.
14.如图所示,已知矩形ABCD周长为24cm,对角线交于点O,OE⊥DC于点E,OF⊥AD于点F,OF-OE=2cm,则AB=______,BC=______.
若矩形两对角线相交所成的角等于120°,较长边为6cm,则该矩形的对角线长为 cm;
综合题
16. 如图,在四边形ABCD中,AD∥BC,E、F为AB上两点,且△DAF≌△CBE.
求证:(1)∠A=90°;
(2)四边形ABCD是矩形.
17.如图,△ABC中,D为边AC的中点,过点D作MN∥BC,CE平分∠ACB交MN于E,CF平分∠ACG交MN于F,求证:(1)ED=DF;(2)四边形AECF为矩形.
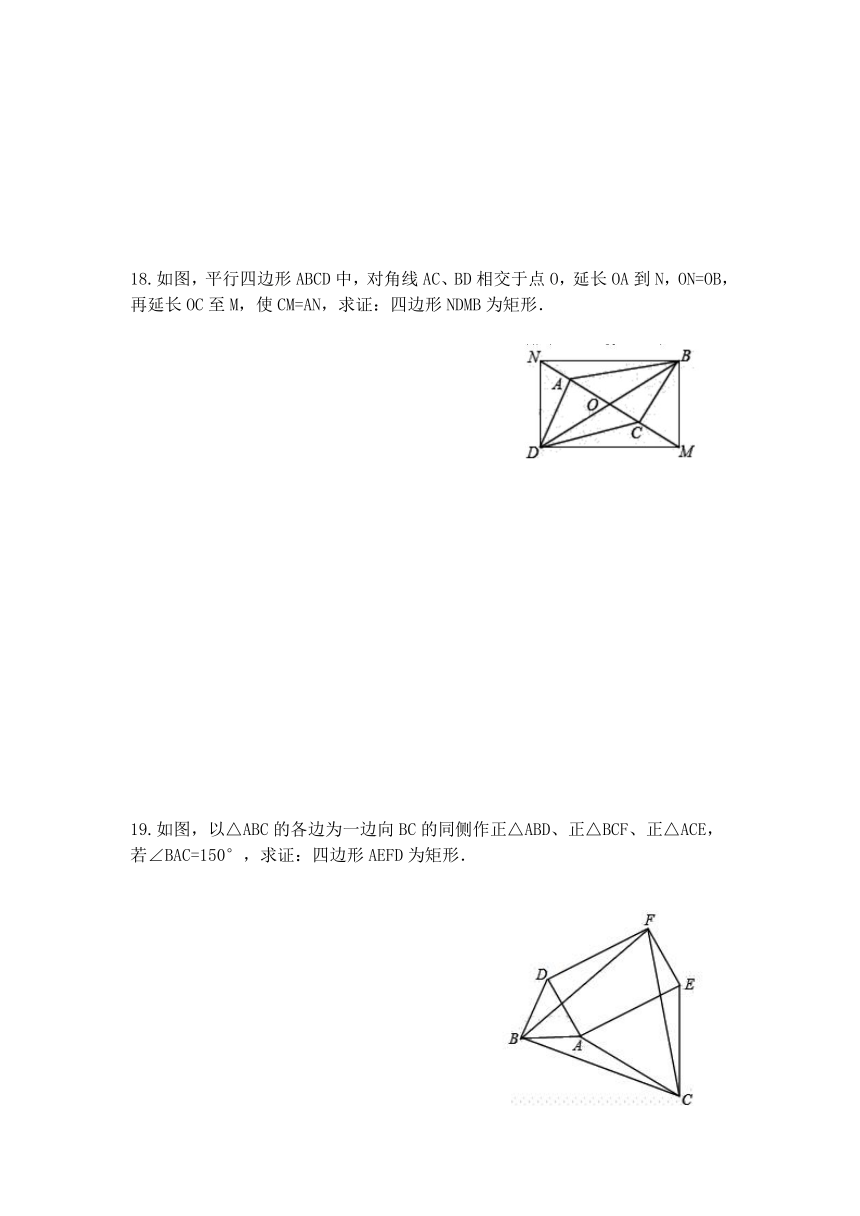
18.如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,ON=OB,再延长OC至M,使CM=AN,求证:四边形NDMB为矩形.
19.如图,以△ABC的各边为一边向BC的同侧作正△ABD、正△BCF、正△ACE,若∠BAC=150°,求证:四边形AEFD为矩形.
20.如图,在△ABC中,D是AC的中点,E是线段BC延长线上的一点,过点A作AF∥BE,交ED的延长线于点F,连接AE,CF.
(1)求证:AF=CE;
(2)如果AC=EF,则四边形AFCE是矩形.
18.2 特殊的平行四边形
矩形的判定同步测试答案
选择题
1.C 2.B 3.B 4.D 5.C 6.C 7.C 8.C 9.C 10.C
二、填空题
11. 3
12.AC=BD
13.矩;1:2
14.8cm;4cm
15. 4
三、综合题
16.解:(1)∵AD∥BC,
∴∠A+∠B=180°,
∵△DAF≌△CBE,
∴∠A=∠B,
∴2∠A=180°,
∴∠A=90°;
(2)∵AD∥BC,AD=BC,
∴四边形ABCD为平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形
17.(1)∵CE平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ECB,∠ACF=∠FCG,
又∵MN∥BG,
∴∠DEC=∠ECB,∠DFC=∠FCG,
∴∠DEC=∠DCE,∠DFC=∠DCF,
∴DE=DC,DF=DC,
∴DE=DF.
(2)∵D为AC的中点,
∴AD=DC,
又DE=DF,
∴四边形AECF为平行四边形,
∵∠ACE=∠ECB,∠ACF=∠FCG,
∴∠ECF=90°,
∴平行四边形AECF为矩形
18.证明:∵四边形ABCD为平行四边形,
∴AO=OC,OD=OB,
∵AN=CM ON=OB,
∴ON=OM=OD=OB,
∴四边形NDMB为平行四边形,
∵MN=BD,
∴平行四边形NDMB为矩形
19.证明:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,
∴△ABC≌△DBF,
∴AC=DF=AE,
同理可证△ABC≌△EFC,
∴AB=EF=AD,
∴四边形DAFEF是平行四边形(两组对边分别相等的四边形是平行四边形)
∵∠BAC=150°,
∴∠DAE=150°﹣∠DAB﹣∠EAC=90°,
∴四边形AEFD为矩形.
20.(1)证明:∵AF∥BE,
∴∠AFD=∠CED,∠FAD=∠DCE,
∵D是AC的中点,
∴AD=DC,
在△FAD和△ECD中
,
∴△FAD≌△ECD(AAS),
∴AF=CE;
(2)证明:∵△FAD≌△ECD,
∴FD=DE,
∵AD=DC,
∴四边形AFCE是平行四边形,
∵AC=EF,
∴平行四边形AFCE是矩形
矩形的判定
选择题
1.下列命题是真命题的是( );
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形
D.对角线互相垂直的四边形是矩形
2.若矩形两邻边的长度之比为2︰3,面积为54cm2, 则其周长( ).
A. 15cm B. 30cm C. 45cm D. 90cm
3.下列叙述中能判定四边形是矩形的个数是( )
①对角线互相平分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线互相平分且相等的四边形.
A.1 B.2 C.3 D.4
4.如图所示,在矩形ABCD中,E是BC的中点,AE=AD=2,则AC的长是( )
A. B.4 C. 2 D.
5.下列识别图形不正确的是( )
A.有一个角是直角的平行四边形是矩形
B.有三个角是直角的四边形是矩形
C.对角线相等的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
6.四边形ABCD的对角线相交于点O,下列条件不能判定它是矩形的是( )
A.AB=CD,AB∥CD,∠BAD=90°
B.AO=CO,BO=DO,AC=BD
C.∠BAD=∠ABC=90°,∠BCD+∠ADC=180°
D.∠BAD=∠BCD,∠ABC=∠ADC=90°
7.矩形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相垂直
8.两条平行线被第三条直线所截,两组内错角的平分线相交所成的四边形是( )
A. 一般平行四边形 B. 菱形
C. 矩形 D. 正方形
9..如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥CD???B.AB=CD????C.AC⊥BD???D.AC=BD
10.平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC????B.AC=BD????C.AC⊥BD???D.AB⊥BD
填空题
11.直角△ABC中,∠BAC=90°,D、E、F分别为AB、BC、AC的中点,
已知DF=3,则AE= ______ .
如图,在?ABCD中,对角线AC与BD相交于点O,在不添加任何辅助线和字母的情况下,请添加一个条件,使?ABCD变为矩形,需添加的条件是 ______ (写出一个即可)
13.若四边形ABCD的对角线AC,BD相等,且互相平分于点O,则四边形ABCD是_____形,若∠AOB=60°,那么AB:AC=______.
14.如图所示,已知矩形ABCD周长为24cm,对角线交于点O,OE⊥DC于点E,OF⊥AD于点F,OF-OE=2cm,则AB=______,BC=______.
若矩形两对角线相交所成的角等于120°,较长边为6cm,则该矩形的对角线长为 cm;
综合题
16. 如图,在四边形ABCD中,AD∥BC,E、F为AB上两点,且△DAF≌△CBE.
求证:(1)∠A=90°;
(2)四边形ABCD是矩形.
17.如图,△ABC中,D为边AC的中点,过点D作MN∥BC,CE平分∠ACB交MN于E,CF平分∠ACG交MN于F,求证:(1)ED=DF;(2)四边形AECF为矩形.
18.如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,ON=OB,再延长OC至M,使CM=AN,求证:四边形NDMB为矩形.
19.如图,以△ABC的各边为一边向BC的同侧作正△ABD、正△BCF、正△ACE,若∠BAC=150°,求证:四边形AEFD为矩形.
20.如图,在△ABC中,D是AC的中点,E是线段BC延长线上的一点,过点A作AF∥BE,交ED的延长线于点F,连接AE,CF.
(1)求证:AF=CE;
(2)如果AC=EF,则四边形AFCE是矩形.
18.2 特殊的平行四边形
矩形的判定同步测试答案
选择题
1.C 2.B 3.B 4.D 5.C 6.C 7.C 8.C 9.C 10.C
二、填空题
11. 3
12.AC=BD
13.矩;1:2
14.8cm;4cm
15. 4
三、综合题
16.解:(1)∵AD∥BC,
∴∠A+∠B=180°,
∵△DAF≌△CBE,
∴∠A=∠B,
∴2∠A=180°,
∴∠A=90°;
(2)∵AD∥BC,AD=BC,
∴四边形ABCD为平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形
17.(1)∵CE平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ECB,∠ACF=∠FCG,
又∵MN∥BG,
∴∠DEC=∠ECB,∠DFC=∠FCG,
∴∠DEC=∠DCE,∠DFC=∠DCF,
∴DE=DC,DF=DC,
∴DE=DF.
(2)∵D为AC的中点,
∴AD=DC,
又DE=DF,
∴四边形AECF为平行四边形,
∵∠ACE=∠ECB,∠ACF=∠FCG,
∴∠ECF=90°,
∴平行四边形AECF为矩形
18.证明:∵四边形ABCD为平行四边形,
∴AO=OC,OD=OB,
∵AN=CM ON=OB,
∴ON=OM=OD=OB,
∴四边形NDMB为平行四边形,
∵MN=BD,
∴平行四边形NDMB为矩形
19.证明:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,
∴△ABC≌△DBF,
∴AC=DF=AE,
同理可证△ABC≌△EFC,
∴AB=EF=AD,
∴四边形DAFEF是平行四边形(两组对边分别相等的四边形是平行四边形)
∵∠BAC=150°,
∴∠DAE=150°﹣∠DAB﹣∠EAC=90°,
∴四边形AEFD为矩形.
20.(1)证明:∵AF∥BE,
∴∠AFD=∠CED,∠FAD=∠DCE,
∵D是AC的中点,
∴AD=DC,
在△FAD和△ECD中
,
∴△FAD≌△ECD(AAS),
∴AF=CE;
(2)证明:∵△FAD≌△ECD,
∴FD=DE,
∵AD=DC,
∴四边形AFCE是平行四边形,
∵AC=EF,
∴平行四边形AFCE是矩形
