北师大版七年级数学下册 4.5 利用三角形全等测距离 同步练习(解析版)
文档属性
| 名称 | 北师大版七年级数学下册 4.5 利用三角形全等测距离 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 272.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 22:34:51 | ||
图片预览


文档简介
4.5利用三角形全等测距离
一、选择题
1.有一个小口瓶(如图所示),想知道它的内径是多少,但是尺子不能伸到里边直接测,于是拿两根长度相同的细木条,把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
2.利用三角形全等测量距离的原理是( )
A.全等三角形对应角相等 B.全等三角形对应边相等
C.大小和形状相同的两个三角形全等 D.三边对应相等的两个三角形全等
3.如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长;判定△EDC≌△ABC的理由是 ( )
A.SSS B.ASA C.AAS D.SAS
【
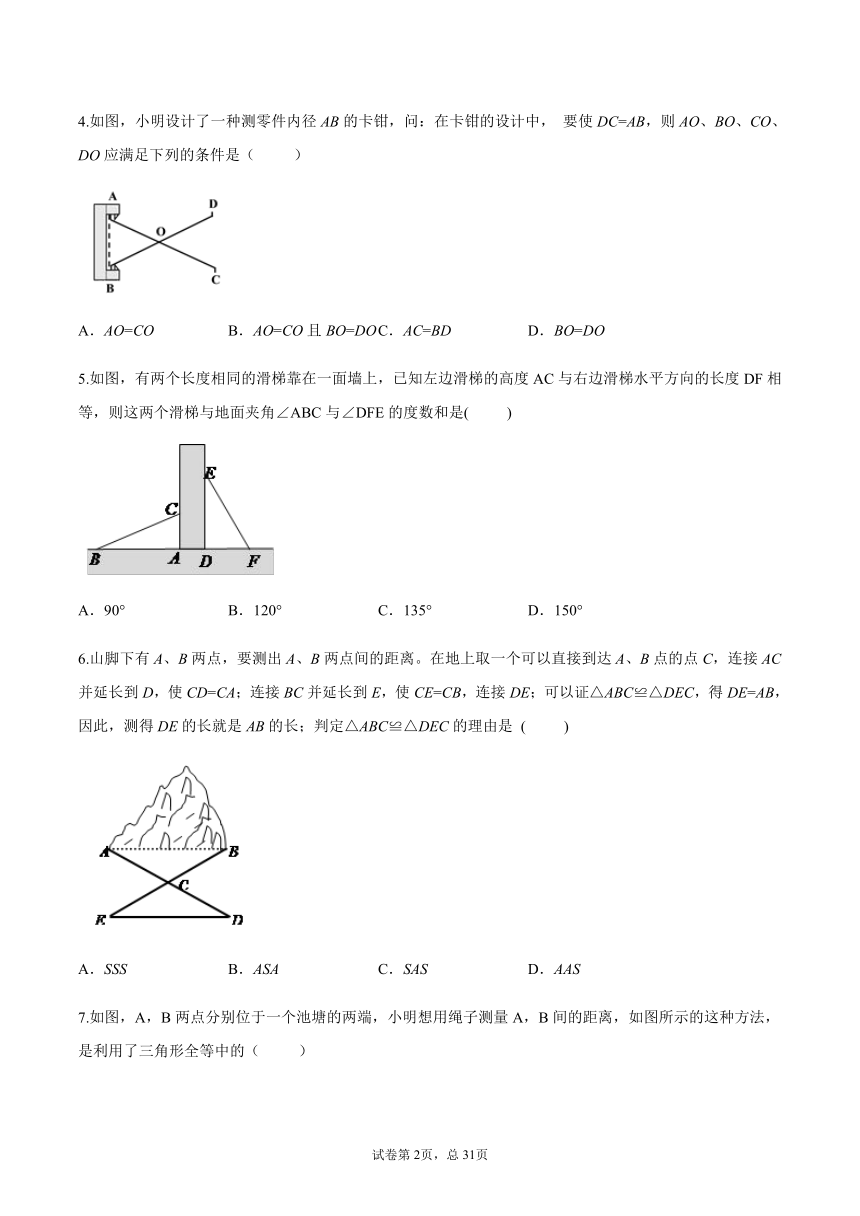
4.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,则AO、BO、CO、DO应满足下列的条件是( )
A.AO=CO B.AO=CO且BO=DO C.AC=BD D.BO=DO
5.如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.90° B.120° C.135° D.150°
6.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE;可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长;判定△ABC≌△DEC的理由是 ( )
A.SSS B.ASA C.SAS D.AAS
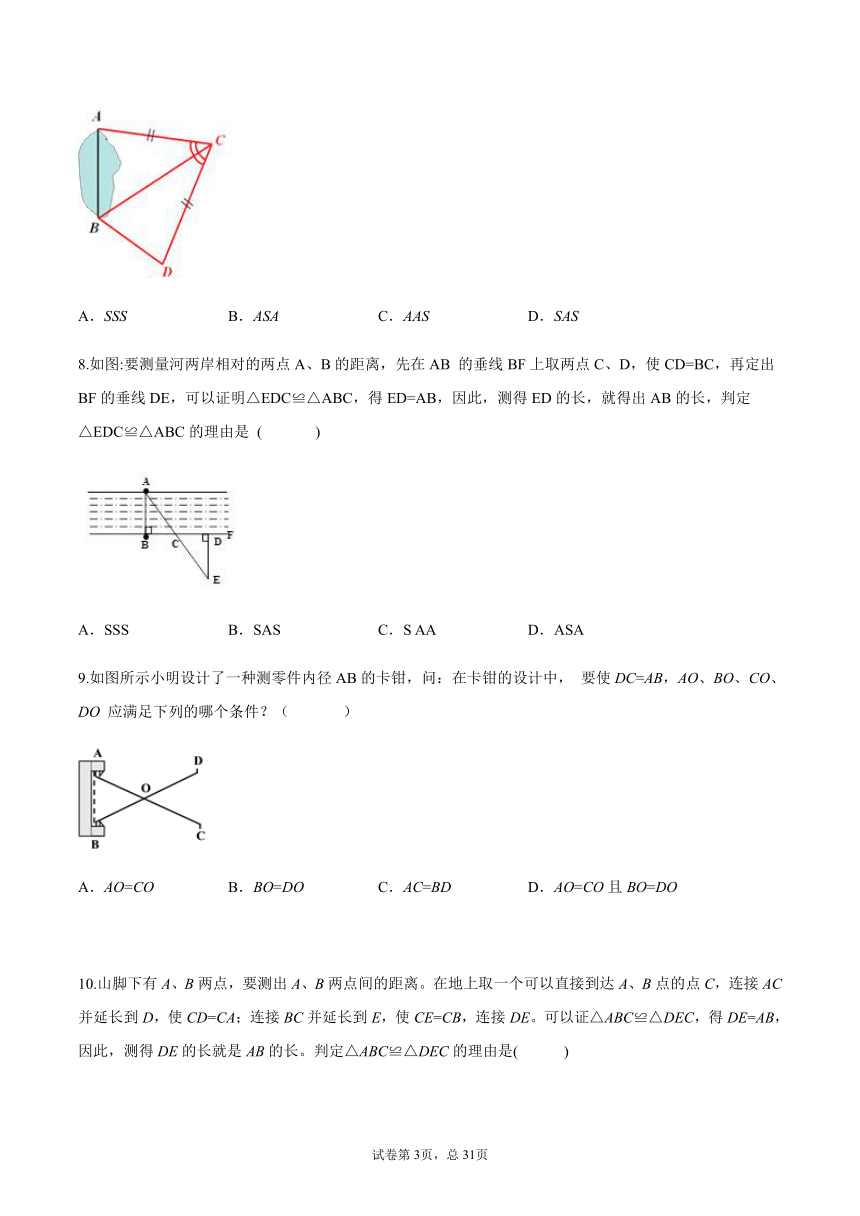
7.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
8.如图:要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长,就得出AB的长,判定△EDC≌△ABC的理由是 ( )
A.SSS B.SAS C.S AA D.ASA
9.如图所示小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO B.BO=DO C.AC=BD D.AO=CO且BO=DO
10.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE。可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长。判定△ABC≌△DEC的理由是( )
A.SSS B.ASA C.AAS D.SAS
11.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A.边角边 B.角边角 C.边边边 D.边边角
12.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
13.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
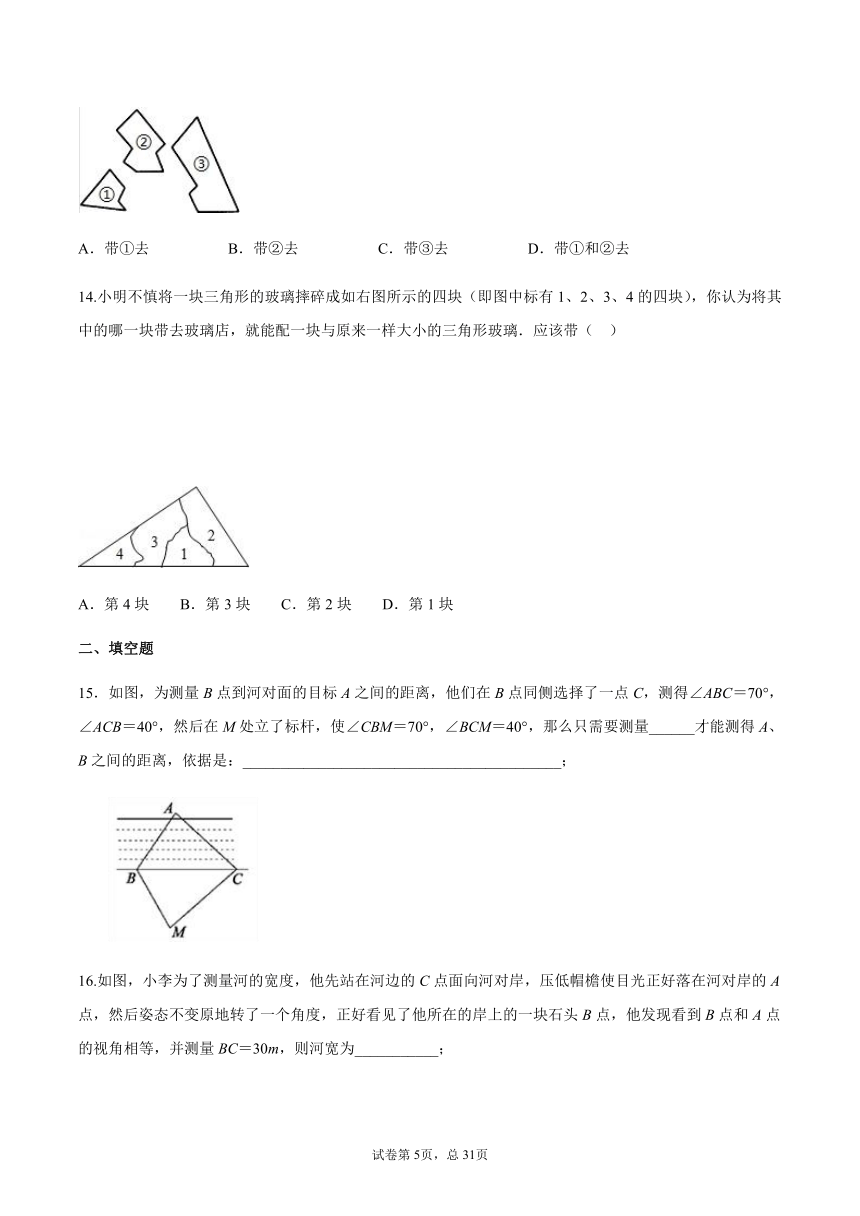
14.小明不慎将一块三角形的玻璃摔碎成如右图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )
A.第4块 B.第3块 C.第2块 D.第1块
二、填空题
15.如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么只需要测量______才能测得A、B之间的距离,依据是:__________________________________________;
16.如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m,则河宽为___________;
17.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
18.如图,某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD=42°,看到烟囱底部C的俯角∠CAD也是42°,如果楼AE高是15米,那么烟囱BC高__米.
19.如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30cm,则由以上信息可推得CB的长度也为30cm,依据是______.
20.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站_____千米的地方.
21.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第_____块。
三、解答题
22.如图所示,小王想测量小口瓶下半部的内径,他把两根长度相等的钢条AA′,BB′的中点连在一起,A,B两点可活动,使M,N卡在瓶口的内壁上,A′,B′卡在小口瓶下半部的瓶壁上,然后量出AB的长度,就可量出小口瓶下半部的内径,请说明理由.
23.为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使.测得CD=35m,就确定了AB也是35m,说明其中的理由;
24.如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
25.如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,你发现线段AD与BE有什么大小关系?试说明你的结论.
(
D
E
CA
A
B
)
26.如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
27.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
28.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
29.如图,由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定是否合乎要求,并说明理由.(电线杆的粗细忽略不计)
参考答案
一、选择题
1.有一个小口瓶(如图所示),想知道它的内径是多少,但是尺子不能伸到里边直接测,于是拿两根长度相同的细木条,把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
【答案】A
【解析】
根据SAS得:△OAB≌△OCD.则AB=CD.故选A.
2.利用三角形全等测量距离的原理是( )
A.全等三角形对应角相等 B.全等三角形对应边相等
C.大小和形状相同的两个三角形全等 D.三边对应相等的两个三角形全等
【答案】B
【解析】利用三角形全等测量距离,是指无法直接测量时,我们通过构造全等的方法,然后借助全等三角形对应边相等,间接测量距离,故选B.
3.如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长;判定△EDC≌△ABC的理由是 ( )
A.SSS B.ASA C.AAS D.SAS
【答案】B
【解析】
由题意得: 根据ASA得:△EDC≌△ABC.故选B.
4.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,则AO、BO、CO、DO应满足下列的条件是( )
A.AO=CO B.AO=CO且BO=DO C.AC=BD D.BO=DO
【答案】B
【解析】
如图,连接CD.
AO=CO且BO=DO,(对顶角相等) ,所以 ,则 DC=AB .故选B.
5.如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.90° B.120° C.135° D.150°
【答案】A
【解析】
由题意得: ,在 和中, 所以 .所以.故选A.
6.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE;可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长;判定△ABC≌△DEC的理由是 ( )
A.SSS B.ASA C.SAS D.AAS
【答案】C
【解析】
因为CD=CA, CE=CB, ,所以△ABC≌△DEC(SAS)故选C.
7.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
【答案】D
【解析】
【分析】
利用全等三角形的判定定理可得以证明.
【详解】
由题意可得:
∴△ACB ≌△DCB(SAS)
∴AB = DB故选D.
8.如图:要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长,就得出AB的长,判定△EDC≌△ABC的理由是 ( )
A.SSS B.SAS C.S AA D.ASA
【答案】D
【解析】
由已知可以得到∠ABC=∠BDE,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC.
解:∵BF⊥AB,DE⊥BD
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA)故选D.
“点睛”解答本题需注意根据垂直定义得到的条件,以及隐含的对顶角相等,观察图形,找着隐含条件是十分重要的.
9.如图所示小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO B.BO=DO C.AC=BD D.AO=CO且BO=DO
【答案】D
【解析】
三角形全等,需要三个条件,
各选项中,只给出了一个条件,再加上隐含的对顶角相等,才两个条件,故不正确。
对于选项D,可得:
AO=CO且BO=DO(已知)
∠AOB=∠COD(对顶角相等)
∴△ACB ≌△DCE(SAS)
∴DC = AB,故选D。
点睛:对于测量不可到达的两个点之间的距离时,有多种方法,而用三角形全等法去测量,也有着不同的解法,只要能够达到测量的目标就行。对于三角形全等的判定,必须在三个条件,其中可以包含原题中隐含的条件.
10.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE。可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长。判定△ABC≌△DEC的理由是( )
A.SSS B.ASA C.AAS D.SAS
【答案】D
【解析】
由原题可得:
CD=CA
∠ACB=∠DCE
CE=CB
∴△ACB ≌△DCE(SAS)
∴DE = AB
故选D。
11.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A.边角边 B.角边角 C.边边边 D.边边角
【答案】B
【解析】
试题分析:由已知可以得到∠ABC=∠BDE=90°,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC.
故选B.
考点:全等三角形的应用.
12.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
【答案】B
【解析】
试题分析:先根据BC=EF,AC=DF判断出Rt△ABC≌Rt△DEF,再根据全等三角形的性质可知,∠1=∠4,再由直角三角形的两锐角互余即可解答.
解:∵滑梯、墙、地面正好构成直角三角形,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF,
∴∠2=∠3,∠1=∠4,
∵∠3+∠4=90°,
∴∠ABC+∠DFE=90°.
故选B.
点评:本题考查的是全等三角形的判定及性质,直角三角形的性质,属较简单题目.
13.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
【答案】C
【解析】
【分析】
根据三角形全等的判定方法逐项分析即可得.
【详解】
A、带①去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,不可得到与原来一样的三角形,此项错误
B、带②去,仅保留了原三角形的部分边,不符合任何判定方法,不可得到与原来一样的三角形,此项错误
C、带③去,不仅保留了原三角形的两个角,还保留了其中的一条边,符合判定定理,可得到与原来一样的三角形,此项正确
D、带①和②去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,不可得到与原来一样的三角形,此项错误
故选:C.
【点睛】
本题考查了三角形全等的判定定理,理解题意,掌握判定定理是解题关键.
14.小明不慎将一块三角形的玻璃摔碎成如右图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )
A.第4块 B.第3块 C.第2块 D.第1块
【答案】C
【解析】
试题分析:本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选C.
点评:本题主要考查三角形全等的判定,看这4块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
二、填空题
15.如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么只需要测量______才能测得A、B之间的距离,依据是:__________________________________________;
【答案】BM △ABC≌△MBC(ASA),全等三角形的对应边相等;
【解析】
在 中,∠ABC=∠CBM=70°,BC=BC,∠ACB=∠BCM=40°,所以△ABC≌△MBC(ASA),根据全等三角形的对应边相等,所以AB=BM
故答案:(1). BM (2). △ABC≌△MBC(ASA),全等三角形的对应边相等.
16.如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m,则河宽为___________;
【答案】30m;
【解析】
由题意得:在 中, ,,
故答案:30m.
17.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
【答案】6米
【解析】
试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),
所以小杨树的高为6米.
故答案为:6米.
18.如图,某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD=42°,看到烟囱底部C的俯角∠CAD也是42°,如果楼AE高是15米,那么烟囱BC高__米.
【答案】30
【解析】
∵∠BAD=∠CAD=42°,
∴AD是∠BAC的平分线.
∵AD⊥BC,
∴BD=CD.
∴BC=2CD=2AE=30.
故烟囱的高度为30米.故答案为:30.
点睛:本题主要考查了等腰三角形的判定及性质的应用.判定三角形为等腰三角形需要弄清楚三角形内角或边之间的关系.
19.如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30cm,则由以上信息可推得CB的长度也为30cm,依据是______.
【答案】全等三角形对应边相等.
【解析】
由图可知,AD∥CB,
可证明△ADE和△CBE中,∠A=∠B(两直线平行,内错角相等),∠D=∠C(两直线平行,内错角相等),∠AED=∠CEB(对顶角相等),则△ADE≌△CBE,所以AD=BE=30cm,运用了全等三角形对应边相等的性质,故答案为: 全等三角形对应边相等.
20.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站_____千米的地方.
【答案】12
【解析】
设AE=x千米,则BE=(36-x)千米,
在Rt△AEC中,CE2=AE2+AC2=x2+242,在Rt△BED中,
DE2=BE2+BD2=+122,
∵CE=ED,∴x2+242=+122,解得x=12,所以E站应建在距A站12千米的地方,能使蔬菜基地C,D到E的距离相等,故答案为12.
21.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第_____块。
【答案】4
【解析】
【分析】
由全等三角形的判定条件可得结论.
【详解】
∵第1、2、3块不具备全等三角形的判定条件,
∴不能带它们去
∵第4块具有完整的两角及夹边,符合ASA,
∴带第4块去能配一块与原来一样大小的三角形
故填:4.
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的几个判定定理是解题的关键.
三、解答题
22.如图所示,小王想测量小口瓶下半部的内径,他把两根长度相等的钢条AA′,BB′的中点连在一起,A,B两点可活动,使M,N卡在瓶口的内壁上,A′,B′卡在小口瓶下半部的瓶壁上,然后量出AB的长度,就可量出小口瓶下半部的内径,请说明理由.
【答案】见解析
【解析】
分析:根据线段中点的性质,得到两组边对应相等,再根据对顶角相等得到三角形全等的第三个条件,于是得到三角形全等。
本题解析:
∵AA′,BB′的中点为O
∴OA=OA′,OB=OB′
又∠AOB=∠A′OB′
∴△A′OB′≌△AOB,
∴AB=A′B′.
23.为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使.测得CD=35m,就确定了AB也是35m,说明其中的理由;
【答案】35 m
【解析】
分析:根据题中条件可以直接得到两组边对应相等,再根据对顶角相等得到三角形全等的第三个条件,于是根据SAS可得到三角形全等,全等三角形的对应边相等,得结论.
本题解析:
∵PA=PD PC=PB
又∠APB=∠CPD
∴△APB≌△DPC,
∴AB=CD=35 m.
24.如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
【答案】a米.
【解析】
试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
∴∠CBM=∠NBM=45°,
∴∠AMB=90°-45°,即∠ABM=∠AMB,
∴AB=AM=a,即房间的宽AB是a米.
25.如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,你发现线段AD与BE有什么大小关系?试说明你的结论.
(
D
E
CA
A
B
)
【答案】,见解析
【解析】解:
易发现AD与BE所在的△ABD与△BCE在滑动过程中始终全等,因而AD=BE.
26.如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
【答案】证明见解析.
【解析】
试题分析:根据SAS即可证明△ACB≌△ACD,由此即可解决问题.
试题解析:因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD.
27.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
【答案】楼高AB是26米.
【解析】
试题分析: 因为∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
所以∠DCP=∠APB=54°,根据,,判定△CPD≌△PAB,根据全等三角形的性质进而得出AB的长.
试题解析:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中,
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
28.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
【答案】(1)5;(2)见解析.
【解析】
【分析】
(1)根据全等三角形对应角相等可得AB=DE;
(2)利用“角边角”证明Rt△ABC和Rt△EDC全等,再根据全等三角形对应边相等解答.
【详解】
(1)由题意知,DE=AB=5米,即河的宽度是5米,
故答案是:5;
(2)证明:由作法知,BC=DC,∠ABC=∠EDC=90°,
在△ABC和△EDC中,,
∴△ABC≌△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
【点睛】
本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.
29.如图,由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定是否合乎要求,并说明理由.(电线杆的粗细忽略不计)
【答案】合乎要求.理由见解析.
【解析】
试题分析:根据题意,证明△ABO≌△ACO即可得解.
试题解析:合乎要求.理由如下:
在△ABO和△ACO中,
所以△ABO≌△ACO(SAS).
所以∠BAO=∠CAO.所以合乎要求.
试卷第1页,总3页
试卷第1页,总3页
一、选择题
1.有一个小口瓶(如图所示),想知道它的内径是多少,但是尺子不能伸到里边直接测,于是拿两根长度相同的细木条,把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
2.利用三角形全等测量距离的原理是( )
A.全等三角形对应角相等 B.全等三角形对应边相等
C.大小和形状相同的两个三角形全等 D.三边对应相等的两个三角形全等
3.如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长;判定△EDC≌△ABC的理由是 ( )
A.SSS B.ASA C.AAS D.SAS
【
4.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,则AO、BO、CO、DO应满足下列的条件是( )
A.AO=CO B.AO=CO且BO=DO C.AC=BD D.BO=DO
5.如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.90° B.120° C.135° D.150°
6.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE;可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长;判定△ABC≌△DEC的理由是 ( )
A.SSS B.ASA C.SAS D.AAS
7.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
8.如图:要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长,就得出AB的长,判定△EDC≌△ABC的理由是 ( )
A.SSS B.SAS C.S AA D.ASA
9.如图所示小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO B.BO=DO C.AC=BD D.AO=CO且BO=DO
10.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE。可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长。判定△ABC≌△DEC的理由是( )
A.SSS B.ASA C.AAS D.SAS
11.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A.边角边 B.角边角 C.边边边 D.边边角
12.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
13.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
14.小明不慎将一块三角形的玻璃摔碎成如右图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )
A.第4块 B.第3块 C.第2块 D.第1块
二、填空题
15.如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么只需要测量______才能测得A、B之间的距离,依据是:__________________________________________;
16.如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m,则河宽为___________;
17.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
18.如图,某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD=42°,看到烟囱底部C的俯角∠CAD也是42°,如果楼AE高是15米,那么烟囱BC高__米.
19.如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30cm,则由以上信息可推得CB的长度也为30cm,依据是______.
20.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站_____千米的地方.
21.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第_____块。
三、解答题
22.如图所示,小王想测量小口瓶下半部的内径,他把两根长度相等的钢条AA′,BB′的中点连在一起,A,B两点可活动,使M,N卡在瓶口的内壁上,A′,B′卡在小口瓶下半部的瓶壁上,然后量出AB的长度,就可量出小口瓶下半部的内径,请说明理由.
23.为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使.测得CD=35m,就确定了AB也是35m,说明其中的理由;
24.如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
25.如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,你发现线段AD与BE有什么大小关系?试说明你的结论.
(
D
E
CA
A
B
)
26.如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
27.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
28.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
29.如图,由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定是否合乎要求,并说明理由.(电线杆的粗细忽略不计)
参考答案
一、选择题
1.有一个小口瓶(如图所示),想知道它的内径是多少,但是尺子不能伸到里边直接测,于是拿两根长度相同的细木条,把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
【答案】A
【解析】
根据SAS得:△OAB≌△OCD.则AB=CD.故选A.
2.利用三角形全等测量距离的原理是( )
A.全等三角形对应角相等 B.全等三角形对应边相等
C.大小和形状相同的两个三角形全等 D.三边对应相等的两个三角形全等
【答案】B
【解析】利用三角形全等测量距离,是指无法直接测量时,我们通过构造全等的方法,然后借助全等三角形对应边相等,间接测量距离,故选B.
3.如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长;判定△EDC≌△ABC的理由是 ( )
A.SSS B.ASA C.AAS D.SAS
【答案】B
【解析】
由题意得: 根据ASA得:△EDC≌△ABC.故选B.
4.如图,小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,则AO、BO、CO、DO应满足下列的条件是( )
A.AO=CO B.AO=CO且BO=DO C.AC=BD D.BO=DO
【答案】B
【解析】
如图,连接CD.
AO=CO且BO=DO,(对顶角相等) ,所以 ,则 DC=AB .故选B.
5.如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.90° B.120° C.135° D.150°
【答案】A
【解析】
由题意得: ,在 和中, 所以 .所以.故选A.
6.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE;可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长;判定△ABC≌△DEC的理由是 ( )
A.SSS B.ASA C.SAS D.AAS
【答案】C
【解析】
因为CD=CA, CE=CB, ,所以△ABC≌△DEC(SAS)故选C.
7.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
【答案】D
【解析】
【分析】
利用全等三角形的判定定理可得以证明.
【详解】
由题意可得:
∴△ACB ≌△DCB(SAS)
∴AB = DB故选D.
8.如图:要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长,就得出AB的长,判定△EDC≌△ABC的理由是 ( )
A.SSS B.SAS C.S AA D.ASA
【答案】D
【解析】
由已知可以得到∠ABC=∠BDE,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC.
解:∵BF⊥AB,DE⊥BD
∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE
∴△EDC≌△ABC(ASA)故选D.
“点睛”解答本题需注意根据垂直定义得到的条件,以及隐含的对顶角相等,观察图形,找着隐含条件是十分重要的.
9.如图所示小明设计了一种测零件内径AB的卡钳,问:在卡钳的设计中, 要使DC=AB,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO B.BO=DO C.AC=BD D.AO=CO且BO=DO
【答案】D
【解析】
三角形全等,需要三个条件,
各选项中,只给出了一个条件,再加上隐含的对顶角相等,才两个条件,故不正确。
对于选项D,可得:
AO=CO且BO=DO(已知)
∠AOB=∠COD(对顶角相等)
∴△ACB ≌△DCE(SAS)
∴DC = AB,故选D。
点睛:对于测量不可到达的两个点之间的距离时,有多种方法,而用三角形全等法去测量,也有着不同的解法,只要能够达到测量的目标就行。对于三角形全等的判定,必须在三个条件,其中可以包含原题中隐含的条件.
10.山脚下有A、B两点,要测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE。可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长。判定△ABC≌△DEC的理由是( )
A.SSS B.ASA C.AAS D.SAS
【答案】D
【解析】
由原题可得:
CD=CA
∠ACB=∠DCE
CE=CB
∴△ACB ≌△DCE(SAS)
∴DE = AB
故选D。
11.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
A.边角边 B.角边角 C.边边边 D.边边角
【答案】B
【解析】
试题分析:由已知可以得到∠ABC=∠BDE=90°,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC.
故选B.
考点:全等三角形的应用.
12.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
【答案】B
【解析】
试题分析:先根据BC=EF,AC=DF判断出Rt△ABC≌Rt△DEF,再根据全等三角形的性质可知,∠1=∠4,再由直角三角形的两锐角互余即可解答.
解:∵滑梯、墙、地面正好构成直角三角形,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF,
∴∠2=∠3,∠1=∠4,
∵∠3+∠4=90°,
∴∠ABC+∠DFE=90°.
故选B.
点评:本题考查的是全等三角形的判定及性质,直角三角形的性质,属较简单题目.
13.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
【答案】C
【解析】
【分析】
根据三角形全等的判定方法逐项分析即可得.
【详解】
A、带①去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,不可得到与原来一样的三角形,此项错误
B、带②去,仅保留了原三角形的部分边,不符合任何判定方法,不可得到与原来一样的三角形,此项错误
C、带③去,不仅保留了原三角形的两个角,还保留了其中的一条边,符合判定定理,可得到与原来一样的三角形,此项正确
D、带①和②去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,不可得到与原来一样的三角形,此项错误
故选:C.
【点睛】
本题考查了三角形全等的判定定理,理解题意,掌握判定定理是解题关键.
14.小明不慎将一块三角形的玻璃摔碎成如右图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )
A.第4块 B.第3块 C.第2块 D.第1块
【答案】C
【解析】
试题分析:本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选C.
点评:本题主要考查三角形全等的判定,看这4块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
二、填空题
15.如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么只需要测量______才能测得A、B之间的距离,依据是:__________________________________________;
【答案】BM △ABC≌△MBC(ASA),全等三角形的对应边相等;
【解析】
在 中,∠ABC=∠CBM=70°,BC=BC,∠ACB=∠BCM=40°,所以△ABC≌△MBC(ASA),根据全等三角形的对应边相等,所以AB=BM
故答案:(1). BM (2). △ABC≌△MBC(ASA),全等三角形的对应边相等.
16.如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m,则河宽为___________;
【答案】30m;
【解析】
由题意得:在 中, ,,
故答案:30m.
17.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
【答案】6米
【解析】
试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),
所以小杨树的高为6米.
故答案为:6米.
18.如图,某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD=42°,看到烟囱底部C的俯角∠CAD也是42°,如果楼AE高是15米,那么烟囱BC高__米.
【答案】30
【解析】
∵∠BAD=∠CAD=42°,
∴AD是∠BAC的平分线.
∵AD⊥BC,
∴BD=CD.
∴BC=2CD=2AE=30.
故烟囱的高度为30米.故答案为:30.
点睛:本题主要考查了等腰三角形的判定及性质的应用.判定三角形为等腰三角形需要弄清楚三角形内角或边之间的关系.
19.如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30cm,则由以上信息可推得CB的长度也为30cm,依据是______.
【答案】全等三角形对应边相等.
【解析】
由图可知,AD∥CB,
可证明△ADE和△CBE中,∠A=∠B(两直线平行,内错角相等),∠D=∠C(两直线平行,内错角相等),∠AED=∠CEB(对顶角相等),则△ADE≌△CBE,所以AD=BE=30cm,运用了全等三角形对应边相等的性质,故答案为: 全等三角形对应边相等.
20.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站_____千米的地方.
【答案】12
【解析】
设AE=x千米,则BE=(36-x)千米,
在Rt△AEC中,CE2=AE2+AC2=x2+242,在Rt△BED中,
DE2=BE2+BD2=+122,
∵CE=ED,∴x2+242=+122,解得x=12,所以E站应建在距A站12千米的地方,能使蔬菜基地C,D到E的距离相等,故答案为12.
21.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第_____块。
【答案】4
【解析】
【分析】
由全等三角形的判定条件可得结论.
【详解】
∵第1、2、3块不具备全等三角形的判定条件,
∴不能带它们去
∵第4块具有完整的两角及夹边,符合ASA,
∴带第4块去能配一块与原来一样大小的三角形
故填:4.
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的几个判定定理是解题的关键.
三、解答题
22.如图所示,小王想测量小口瓶下半部的内径,他把两根长度相等的钢条AA′,BB′的中点连在一起,A,B两点可活动,使M,N卡在瓶口的内壁上,A′,B′卡在小口瓶下半部的瓶壁上,然后量出AB的长度,就可量出小口瓶下半部的内径,请说明理由.
【答案】见解析
【解析】
分析:根据线段中点的性质,得到两组边对应相等,再根据对顶角相等得到三角形全等的第三个条件,于是得到三角形全等。
本题解析:
∵AA′,BB′的中点为O
∴OA=OA′,OB=OB′
又∠AOB=∠A′OB′
∴△A′OB′≌△AOB,
∴AB=A′B′.
23.为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使.测得CD=35m,就确定了AB也是35m,说明其中的理由;
【答案】35 m
【解析】
分析:根据题中条件可以直接得到两组边对应相等,再根据对顶角相等得到三角形全等的第三个条件,于是根据SAS可得到三角形全等,全等三角形的对应边相等,得结论.
本题解析:
∵PA=PD PC=PB
又∠APB=∠CPD
∴△APB≌△DPC,
∴AB=CD=35 m.
24.如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
【答案】a米.
【解析】
试题分析:连结BM、MN,由SSS证明≌,可得∠CBM=∠NBM=45°,AB=AM=a.
试题解析:a米.连结BM、MN,
在△MCN中,∠MCN=180°-75°-45°=60°,CM=CN,
∴△MCN是等边三角形,
∴MC=MN,∠CBN=90°,∠BCN=45°,
∴BC=BN,在△MCB和△MNB中,
∴△MCB≌△MNB,
∴∠CBM=∠NBM=45°,
∴∠AMB=90°-45°,即∠ABM=∠AMB,
∴AB=AM=a,即房间的宽AB是a米.
25.如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,你发现线段AD与BE有什么大小关系?试说明你的结论.
(
D
E
CA
A
B
)
【答案】,见解析
【解析】解:
易发现AD与BE所在的△ABD与△BCE在滑动过程中始终全等,因而AD=BE.
26.如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
【答案】证明见解析.
【解析】
试题分析:根据SAS即可证明△ACB≌△ACD,由此即可解决问题.
试题解析:因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD.
27.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
【答案】楼高AB是26米.
【解析】
试题分析: 因为∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
所以∠DCP=∠APB=54°,根据,,判定△CPD≌△PAB,根据全等三角形的性质进而得出AB的长.
试题解析:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中,
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
28.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
【答案】(1)5;(2)见解析.
【解析】
【分析】
(1)根据全等三角形对应角相等可得AB=DE;
(2)利用“角边角”证明Rt△ABC和Rt△EDC全等,再根据全等三角形对应边相等解答.
【详解】
(1)由题意知,DE=AB=5米,即河的宽度是5米,
故答案是:5;
(2)证明:由作法知,BC=DC,∠ABC=∠EDC=90°,
在△ABC和△EDC中,,
∴△ABC≌△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
【点睛】
本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.
29.如图,由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定是否合乎要求,并说明理由.(电线杆的粗细忽略不计)
【答案】合乎要求.理由见解析.
【解析】
试题分析:根据题意,证明△ABO≌△ACO即可得解.
试题解析:合乎要求.理由如下:
在△ABO和△ACO中,
所以△ABO≌△ACO(SAS).
所以∠BAO=∠CAO.所以合乎要求.
试卷第1页,总3页
试卷第1页,总3页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
