人教版八年级数学下册 18.2.3正方形习题课件(共31张PPT)
文档属性
| 名称 | 人教版八年级数学下册 18.2.3正方形习题课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-22 00:00:00 | ||
图片预览







文档简介
课件31张PPT。第十八章 平行四边形18.2.3 正方形新知 1 正方形的定义
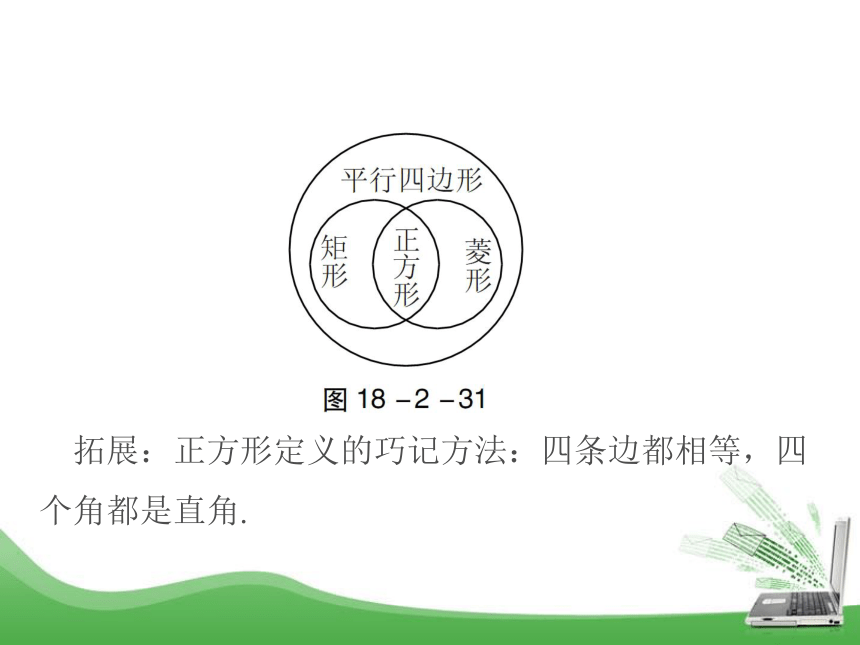
定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形. (1)正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形;(2)既是矩形又是菱形的四边形是正方形;(3)正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形. 正方形、矩形、菱形都是特殊的平行四边形,它们的包含关系如图18-2-31. 拓展:正方形定义的巧记方法:四条边都相等,四个角都是直角. 例题精讲
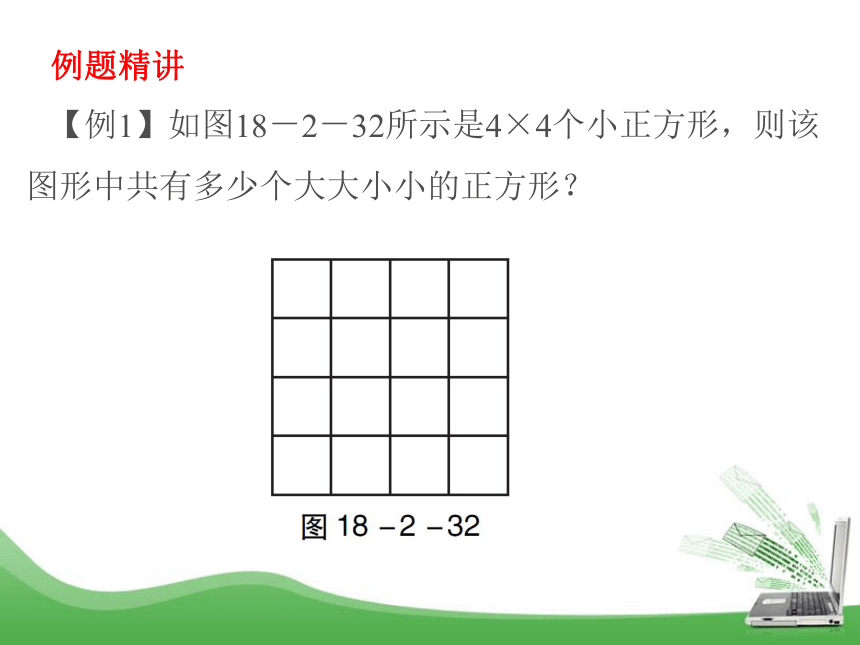
【例1】如图18-2-32所示是4×4个小正方形,则该图形中共有多少个大大小小的正方形?
解 设最小的正方形边长为1,则边长为1的正方形共有16个,边长为2的正方形共有9个,边长为3的正方形共有4个,边长为4的正方形共有1个,总共有16+9+4+1=30(个).
点拨 最小的正方形边长为1,则正方形共有四种情况:1×1,2×2,3×3,4×4.举一反三
1.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分
B. 对角线相等且互相垂直平分
C. 对角线互相平分
D. 四条边相等,四个角相等
2.下列说法正确的是( )
A.对角线相等的四边形是矩形
B. 对角线互相垂直的四边形是正方形
CDC. 平行四边形的对角线平分一组对角
D. 矩形的对角线相等且互相平分
3.正方形具备而菱形不具备的性质是( )
A.四条边都相等
B. 四个角都是直角
C. 对角线互相垂直平分
D. 每条对角线平分一组对角B新知 2 正方形的性质
(1)拓展:一组邻边相等的矩形叫做正方形;
(2)性质:正方形具有平行四边形、矩形、菱形的所有性质;
(3)对称性:正方形是轴对称图形,有四条对称轴.正方形也是中心对称图形.例题精讲
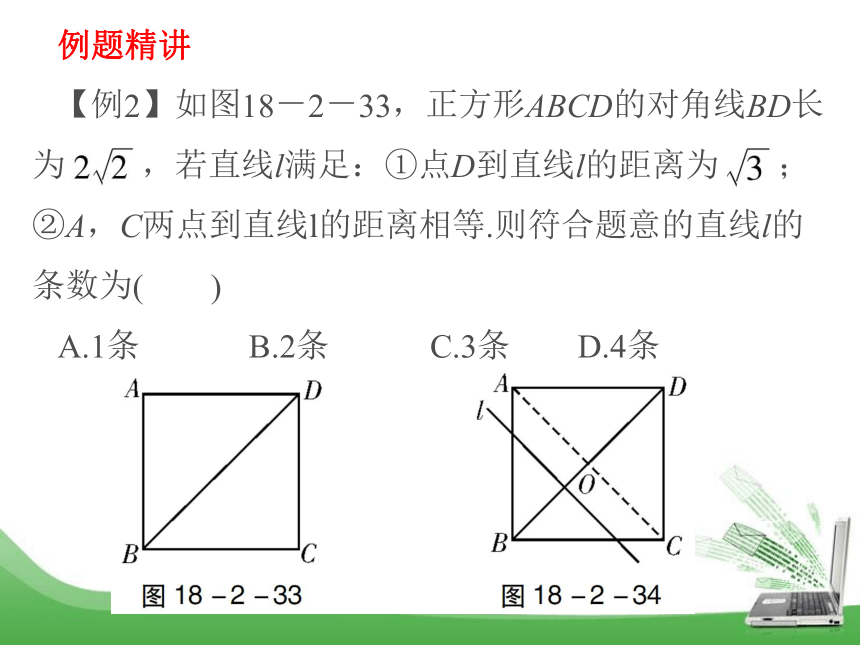
【例2】如图18-2-33,正方形ABCD的对角线BD长为 ,若直线l满足:①点D到直线l的距离为 ;②A,C两点到直线l的距离相等.则符合题意的直线l的条数为( )
A.1条 B.2条 C.3条 D.4条解析 如图18-2-34,连接AC与BD相交于O,
∵正方形ABCD的对角线BD长为2 ,
∴OD= .
∴直线l∥AC并且到D的距离为.
同理,在点D的另一侧还有一条直线满足条件,
故共有2条直线l.
答案 B举一反三
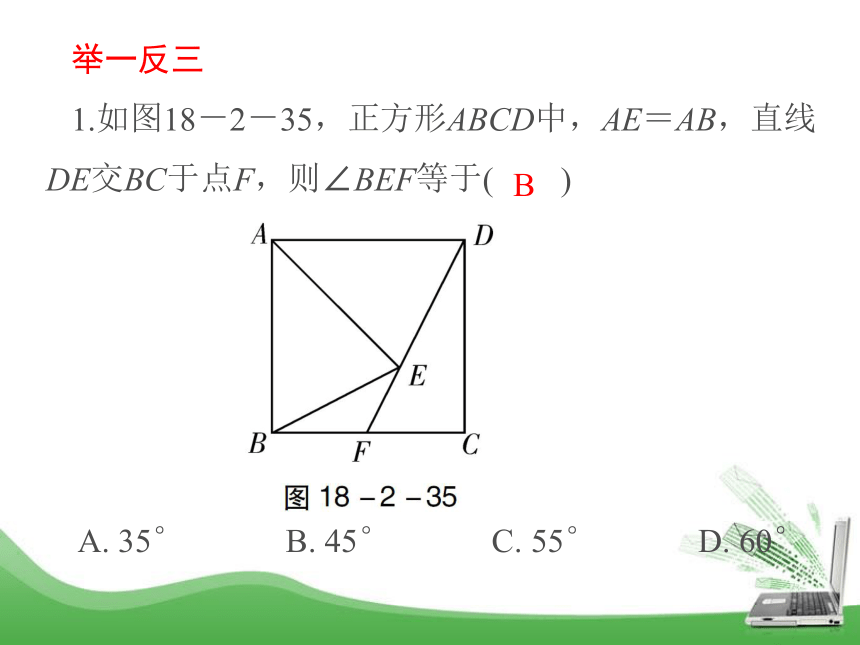
1.如图18-2-35,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF等于( )
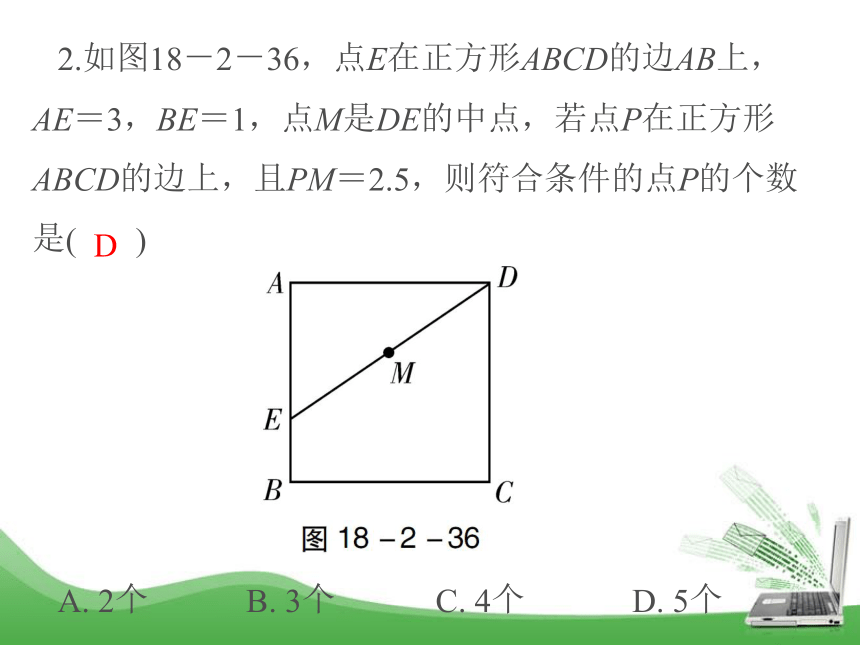
A. 35° B. 45° C. 55° D. 60°B2.如图18-2-36,点E在正方形ABCD的边AB上,AE=3,BE=1,点M是DE的中点,若点P在正方形ABCD的边上,且PM=2.5,则符合条件的点P的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个D新知 3 正方形的判定
判定一个四边形为正方形的主要依据是定义. 主要方法有两条:(1)先证它是矩形,再证有一组邻边相等;(2)先证它是菱形,再证有一个角是直角.
拓展:判定一个四边形为正方形的一般顺序:(1)先证明它是平行四边形;(2)再证有一组邻边相等(或有一个角是直角);(3)最后证有一个角是直角(或有一组邻边相等).例题精讲
【例3】如图18-2-37,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O,连接EF,FG,GH,HE,求证:四边形EFGH是正方形. 解析 先证明△AEH≌△BFE≌△CGF≌△DHG,可得出四边形GHEF是菱形,再根据全等三角形角之间的关系,又可得出菱形的一个角是直角,那么就可得出四边形GHEF是正方形.
证明 ∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
∵HA=EB=FC=GD,
∴AE=BF=CG=DH.
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE.∴四边形EFGH是菱形.
∵△DHG≌△AEH,∴∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°.
∴∠GHE=90°.
∴四边形EFGH是正方形.
点评 本题考查正方形的判定与性质,全等三角形的判定和性质,利用正方形的性质,掌握正方形的判定方法是解决问题的关键.举一反三
1. 如图18-2-38,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
A. 正方形 B. 菱形
C. 矩形 D. 无法确定A2. 已知在四边形ABCD中,AC与BD相交于点O,那么下列条件中能判定这个四边形是正方形的是( )
A. AC=BD,AB∥CD,AB=CD
B. AD∥BC,∠A=∠C
C. AO=BO=CO=DO,AC⊥BD
D. AO=CO,BO=DO,AB=BCC3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图18-2-39),现有下列四种选法,你认为其中错误的是( )
A. ①②
B. ②③
C. ①③
D. ②④B新知4 正方形的面积
正方形的面积的计算方法:
(1)正方形的面积等于其边长的平方;
(2)正方形的面积等于其两条对角线乘积的一半(因为正方形是特殊的菱形,故可以用菱形面积的计算方法来计算).
拓展:周长相等的四边形中,正方形的面积最大【例4】如图18-2-40所示,正方形ABCD的周长为16 cm,顺次连接正方形ABCD各边中点,得到四边形EFGH,则四边形EFGH的周长等于 cm,面积等于 cm2. 解析 由题意可知,四边形EFGH也是正方形,
∵ 正方形ABCD的周长为16 cm,
∴ AB=BC=CD=DA=4 cm.
∴ AH=AE=2 cm.
在Rt△AEH中,EH2=AE2+AH2,
∴ EH2=22+22=8.
∴ EH= cm.
∴ 四边形EFGH的周长为 ×4= (cm),
面积为( )2=8 cm2.
答案 8 1. 如图18-2-41,由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”,其中阴影部分面积为 .12.如图18-2-42,正方形的边长为4 cm,则图中阴影部分的面积为 cm2.( )
A. 8 B. 16 C. 4 D. 无法确定A1. 如图18-2-43,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A. 76 B. 70 C. 48 D. 24A7. (6分)如图KT18-2-17,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.8. (6分)如图KT18-2-18,已知正方形ABCD中,边长为10 cm,点E在AB边上,BE=6 cm.
(1)如果点P在线段BC上以4 cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过1 s后,△BPE与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?解:(1)①∵t=1 s,∴BP=CQ=4×1=4 cm,
∵正方形ABCD中,边长为10 cm,∴PC=BE=6 cm.
又∵正方形ABCD,∴∠B=∠C. △BPE≌△CQP;
②∵vP≠vQ,∴BP≠CQ.
又∵△BPE≌△CQP,∠B=∠C,则BP=PC, 而BP=4t,CP=10-4t,∴4t=10-4t.∴点P,Q运动的时间 ,
∴ (2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动,经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
(2)设经过x s后点P与点Q第一次相遇,由题意,得
4.8x-4x=30,
解得 ∴点P共运动了
∴点P,Q在A点相遇.∴经过 点P与点Q第一次在A点相遇.
定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形. (1)正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形;(2)既是矩形又是菱形的四边形是正方形;(3)正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形. 正方形、矩形、菱形都是特殊的平行四边形,它们的包含关系如图18-2-31. 拓展:正方形定义的巧记方法:四条边都相等,四个角都是直角. 例题精讲
【例1】如图18-2-32所示是4×4个小正方形,则该图形中共有多少个大大小小的正方形?
解 设最小的正方形边长为1,则边长为1的正方形共有16个,边长为2的正方形共有9个,边长为3的正方形共有4个,边长为4的正方形共有1个,总共有16+9+4+1=30(个).
点拨 最小的正方形边长为1,则正方形共有四种情况:1×1,2×2,3×3,4×4.举一反三
1.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分
B. 对角线相等且互相垂直平分
C. 对角线互相平分
D. 四条边相等,四个角相等
2.下列说法正确的是( )
A.对角线相等的四边形是矩形
B. 对角线互相垂直的四边形是正方形
CDC. 平行四边形的对角线平分一组对角
D. 矩形的对角线相等且互相平分
3.正方形具备而菱形不具备的性质是( )
A.四条边都相等
B. 四个角都是直角
C. 对角线互相垂直平分
D. 每条对角线平分一组对角B新知 2 正方形的性质
(1)拓展:一组邻边相等的矩形叫做正方形;
(2)性质:正方形具有平行四边形、矩形、菱形的所有性质;
(3)对称性:正方形是轴对称图形,有四条对称轴.正方形也是中心对称图形.例题精讲
【例2】如图18-2-33,正方形ABCD的对角线BD长为 ,若直线l满足:①点D到直线l的距离为 ;②A,C两点到直线l的距离相等.则符合题意的直线l的条数为( )
A.1条 B.2条 C.3条 D.4条解析 如图18-2-34,连接AC与BD相交于O,
∵正方形ABCD的对角线BD长为2 ,
∴OD= .
∴直线l∥AC并且到D的距离为.
同理,在点D的另一侧还有一条直线满足条件,
故共有2条直线l.
答案 B举一反三
1.如图18-2-35,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF等于( )
A. 35° B. 45° C. 55° D. 60°B2.如图18-2-36,点E在正方形ABCD的边AB上,AE=3,BE=1,点M是DE的中点,若点P在正方形ABCD的边上,且PM=2.5,则符合条件的点P的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个D新知 3 正方形的判定
判定一个四边形为正方形的主要依据是定义. 主要方法有两条:(1)先证它是矩形,再证有一组邻边相等;(2)先证它是菱形,再证有一个角是直角.
拓展:判定一个四边形为正方形的一般顺序:(1)先证明它是平行四边形;(2)再证有一组邻边相等(或有一个角是直角);(3)最后证有一个角是直角(或有一组邻边相等).例题精讲
【例3】如图18-2-37,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O,连接EF,FG,GH,HE,求证:四边形EFGH是正方形. 解析 先证明△AEH≌△BFE≌△CGF≌△DHG,可得出四边形GHEF是菱形,再根据全等三角形角之间的关系,又可得出菱形的一个角是直角,那么就可得出四边形GHEF是正方形.
证明 ∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
∵HA=EB=FC=GD,
∴AE=BF=CG=DH.
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE.∴四边形EFGH是菱形.
∵△DHG≌△AEH,∴∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°.
∴∠GHE=90°.
∴四边形EFGH是正方形.
点评 本题考查正方形的判定与性质,全等三角形的判定和性质,利用正方形的性质,掌握正方形的判定方法是解决问题的关键.举一反三
1. 如图18-2-38,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
A. 正方形 B. 菱形
C. 矩形 D. 无法确定A2. 已知在四边形ABCD中,AC与BD相交于点O,那么下列条件中能判定这个四边形是正方形的是( )
A. AC=BD,AB∥CD,AB=CD
B. AD∥BC,∠A=∠C
C. AO=BO=CO=DO,AC⊥BD
D. AO=CO,BO=DO,AB=BCC3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图18-2-39),现有下列四种选法,你认为其中错误的是( )
A. ①②
B. ②③
C. ①③
D. ②④B新知4 正方形的面积
正方形的面积的计算方法:
(1)正方形的面积等于其边长的平方;
(2)正方形的面积等于其两条对角线乘积的一半(因为正方形是特殊的菱形,故可以用菱形面积的计算方法来计算).
拓展:周长相等的四边形中,正方形的面积最大【例4】如图18-2-40所示,正方形ABCD的周长为16 cm,顺次连接正方形ABCD各边中点,得到四边形EFGH,则四边形EFGH的周长等于 cm,面积等于 cm2. 解析 由题意可知,四边形EFGH也是正方形,
∵ 正方形ABCD的周长为16 cm,
∴ AB=BC=CD=DA=4 cm.
∴ AH=AE=2 cm.
在Rt△AEH中,EH2=AE2+AH2,
∴ EH2=22+22=8.
∴ EH= cm.
∴ 四边形EFGH的周长为 ×4= (cm),
面积为( )2=8 cm2.
答案 8 1. 如图18-2-41,由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”,其中阴影部分面积为 .12.如图18-2-42,正方形的边长为4 cm,则图中阴影部分的面积为 cm2.( )
A. 8 B. 16 C. 4 D. 无法确定A1. 如图18-2-43,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A. 76 B. 70 C. 48 D. 24A7. (6分)如图KT18-2-17,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.8. (6分)如图KT18-2-18,已知正方形ABCD中,边长为10 cm,点E在AB边上,BE=6 cm.
(1)如果点P在线段BC上以4 cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过1 s后,△BPE与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?解:(1)①∵t=1 s,∴BP=CQ=4×1=4 cm,
∵正方形ABCD中,边长为10 cm,∴PC=BE=6 cm.
又∵正方形ABCD,∴∠B=∠C. △BPE≌△CQP;
②∵vP≠vQ,∴BP≠CQ.
又∵△BPE≌△CQP,∠B=∠C,则BP=PC, 而BP=4t,CP=10-4t,∴4t=10-4t.∴点P,Q运动的时间 ,
∴ (2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动,经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
(2)设经过x s后点P与点Q第一次相遇,由题意,得
4.8x-4x=30,
解得 ∴点P共运动了
∴点P,Q在A点相遇.∴经过 点P与点Q第一次在A点相遇.
