人教版高中数学课标教材A版 课件 (96张PPT)选修1-2,2-3
文档属性
| 名称 | 人教版高中数学课标教材A版 课件 (96张PPT)选修1-2,2-3 |  | |
| 格式 | zip | ||
| 文件大小 | 573.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 09:01:12 | ||
图片预览










文档简介
(共96张PPT)
人教版高中数学课标教材(A版)
普通高中课程标准实验教科书选修1-2,2-3
统计案例
简 介
天津八中 陈健
欢迎光临,请多指导 2020年4月21日11时23分
两种统计方法:回归分析和独立性检验都是常用的,在统计学中占有很重要的地位。
统计方法解决问题的过程:
确定总体、选择合适变量、收集数据、分析整理数据、进行决策或预测。
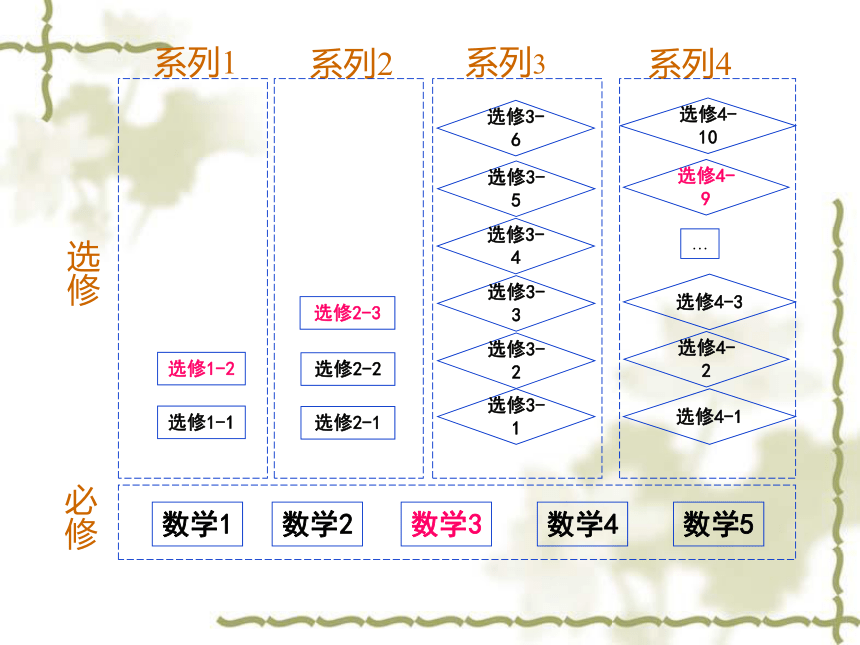
数学1
数学3
数学4
数学2
数学5
选修2-3
选修2-2
选修2-1
选修1-2
选修1-1
选修3-5
选修3-4
选修3-3
选修3-2
选修3-1
选修3-6
选修4-10
选修4-9
…
选修4-3
选修4-2
选修4-1
系列1
系列2
系列3
系列4
选修
必修
数学3:
统计:随机抽样、用样本估计总体、变量间的相关关系
概率:随机事件的概率、古典概型、几何概型
选修2-3(选修1-2):
概率:离散型随机变量及其分布列、二项分布及其应用、离散型随机变量的均值与方差、正态分布
回归分析的基本思想及其初步应用、独立性检验的基本思想及其初步应用
选修4-9 风险与决策
统计学关注的是如何探知由观察数据获取的知识中的不确定性的度量,以及如何明确在最小损失下的最优决策。
教学目标
结构设置与课时分配
回归分析
独立性检验
1.教学目标
通过典型案例的探究,进一步了解线性回归模型的有关知识,包括残差变量的来源、模型诊断的初步知识、应用回归模型解决非线性相关关系问题,进一步了解回归分析的基本思想、方法及其初步应用。
b.通过典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及其初步应用。
1.教学目标
教学目标
结构设置与课时分配
回归分析
独立性检验
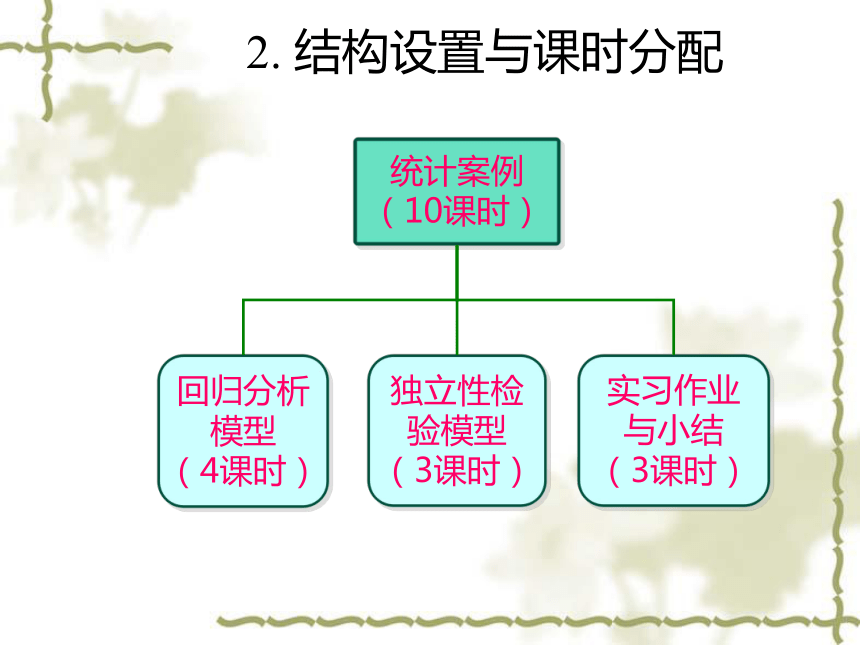
2. 结构设置与课时分配
统计案例
(10课时)
独立性检验模型
(3课时)
回归分析模型
(4课时)
实习作业
与小结
(3课时)
教学目标
结构设置与课时分配
回归分析
独立性检验
3. 回归分析
比《数学3》中“回归”增加的内容
回归分析知识结构图
回归分析教学建议
比《数学3》中“回归”增加的内容
必修《数学3》已学回归内容
画散点图
了解最小二乘法的思想,最小二乘估计计算公式
求回归直线方程
y=bx+a
用回归直线方程解决应用问题(进行预报)
选修《数学2-3》新增内容
引入一元线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用(异常数据识别方法、模型改进)
利用线性回归模型解决一类非线性回归问题
正确理解统计分析方法与结果
3. 回归分析
比《数学3》中“回归”增加的内容
回归分析知识结构图
回归分析教学建议
问题背景分析
线性回归模型
两个变量线性相关
最小二乘法
两个变量非线性相关
非线性回归模型
残差分析
相关指数
散点图
线性相关系数
应用
3. 回归分析
比《数学3》中“回归”增加的内容
回归分析知识结构图
回归分析教学建议
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关系数、相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
函数模型与“回归模型”的关系
函数模型:
回归模型:
样本点在函数曲线上
样本点不在回归函数曲线上
y=f(x)
y=f(x)+e
1993—2019年中国GDP散点图
函数模型与“回归模型”的关系
函数模型:
回归模型:
确定性关系
y=f(x)
y=f(x)+e
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
1):相关关系是一种不确定性关系;
对具有相关关系的两个变量进行统计分析的方法叫回归分析。
2):
注
不确定性关系
函数模型与“回归模型”的关系
函数模型:因变量y完全由自变量x确定
回归模型:预报变量y完全由解释变量x
和随机误差e确定
解释变量x(身高)
随机误差e
(其他所有变量)
预报变量y(体重)
无法得到残差变量的值,但却可以估计它,对它进行分析。
线性回归模型 见选修2-3 P83
y=bx+a+e
y=bx+a+e其中a和b为模型的未知参数,e是y与 之间的误差,通常e称为随机误差。
函数模型与“回归模型”的关系
采用最小二乘法估计模型参数:
(文科不涉及)
这样的方法叫做最小二乘法.(数学3 P92)
问题归结为:a,b取什么值时Q最小,即总体和最小.下面是计算回归方程的斜率和截距的一般公式.
根据最小二乘法和上述公式可以求回归方程.
推导过程见选修2-3 P80
为了衡量预报的精度,需要估计σ2的值?
公式中的分母取n-2是为了达到更好的估计效果。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关系数、相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
1993—2019年中国GDP散点图
散点图与模型的选择
样本点呈条状且散布在某一直线附近(线性)
在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
散点图与模型的选择
散点图帮助确定可供选择模型的范围,而模型的比较则基于残差分析
案例2:红铃虫的产卵数与温度
这些散点更像是集中在一条
指数曲线或二次曲线的附近。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
残差变量与模型选择
残差图帮助确定异常点,以及模型的改进方向。
残差图的制作及作用
在残差图中寻找异常点
可能由错误数据引起
残差图的趋势性分析
趋势性的残差图说明模型有改进的余地
?残差图的制作及作用。(选修2-3P85及教参P97)
?坐标纵轴为残差变量,横轴可以有不同的选择。
?横轴为编号,可以考察残差与编号次序之 间的关系,常用于调查数据错误。
?横轴为解释变量,可以考察残差与解释变量的关系,常用于研究模型是否有改进的余地。
?若模型选择的正确,残差图中的点应该分布在以横轴为中心的带形区域。
在残差图中寻找异常点(远离横轴)
可能由错误数据引起的异常点
异常点
异常点
身高与体重残差图
残差图的趋势性分析
残差图具有趋势性,模型有改进的余地,模型中应该添加二次项
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
残差变量的来源:
?其它因素的影响。如影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素。
?选用的回归模型近似真实模型所引起的误差。
?预报变量的观测误差。身高 y 的测量有误差。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
正确理解相关系数的含义
总偏差平方和
( , )为样本点的中心
x
y
表明两个变量之间的线性相关关系的强弱
?相关指数是度量模型拟合效果的一种指标。
?在线性模型中,它代表解释变量刻画预报变量的能力。
正确理解相关指数的含义
?相关指数是度量模型拟合效果的一种指标。
相关指数越大,模型拟合效果越好。
残差(êi)
平方和
总偏差
平方和
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
注意提炼案例所蕴含的统计思想
在例1结尾提到“用身高预报体重时,需要注意
下列问题:……”,这些论述适用于所有的回归模型。
1.模型的适用性;
2.模型的时间性;
3.样本的取值范围对模型的影响;
4.模型预报结果的正确理解。
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
1.对研究对象的背景分析;
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
某大学8名女大学生的身高与体重
确定变量:
解释变量—x(身高)
预报变量—y(体重)
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
2.利用散点图判断模型类别;
样本点呈条状分布:
身高与体重有比较好的线性相关关系,
因此可以用线性回归方程来近似刻画。
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
3.估计模型参数;
设线性回归模型:y=bx+a+e
采用最小二乘法估计模型参数:
?
=
y
-
?
b
x
(xi-
)(yi-
i=1
∑
n
)
y
x
(xi-
i=1
∑
n
x
)2
?
b
=
=0.849
=-85.712
?
y
=0.849x-85.712
x
=
1
n
i=1
∑
n
xi
y
=
1
n
i=1
∑
n
yi
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
(1)根据散点图来粗略判断它们是否线性相关。
(2)是否可以用线性回归模型来拟合数据
(3)通过残差 来判断模型拟合的效果
这种分析工作称为残差分析
4.残差分析,模型诊断。
4.残差分析,模型诊断。
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差ê -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
4.残差分析,模型诊断。
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差ê -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
总偏差平方和:预报变量的变化程度
回归平方和:解释变量引起的变化程度
残差平方和:残差变量的变化程度
预报变量变化的变化之中能由解释变量引起的比例
R2越大,模型拟合效果越好。
4.残差分析,模型诊断。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
应用统计方法解决实际问题需要注意的问题
通过例2,说明如下结论:
对于同样的数据,有不同的统计方法进行分析,要用最有效的方法分析数据。(残差平方和与R2)
案例2:红铃虫的产卵数与温度(残差分析)
指数模型
二次模型
残差平方和:
相关系数R2 :
1550.538
15448.431
0.98
0.80
应用统计方法解决实际问题需要注意的问题
在讲完例2通过引导学生们讨论“是不是还有其它的效果更好的模型来拟合例2中的数据?”,获得上述结论。
教学目标
结构设置与课时分配
回归分析
独立性检验
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
a. 假设检验问题
假设检验问题由两个互斥的假设构成:
原假设,用H0表示;备择假设,用H1表示。
表达式为: H0:←→ H1:
如:在“吸烟与患肺癌是否有关系”的例子中。
原假设为: H0:吸烟与患肺癌没关系
备择假设为:H1:吸烟与患肺癌有关系
这个假设检验问题可以表示为:
H0:吸烟与患肺癌没关系←→ H1:吸烟与患肺癌有关系
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
b.求解假设检验问题
考虑假设检验问题:H0←→ H1
在H0成立的条件下,构造与H0矛盾的小概率事件;
如果样本使得这个小概率事件发生,就能以一定把握断言H1成立;否则,就说从数据中没有发现充分的证据支持H1成立。
求解思路:
检验问题的解:一个规则,用以判断是H0 还是H1正确。
规则要在获取观测数据之前确定
显著性水平
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
1、提出假设问题
如:在“吸烟与患肺癌是否有关系”的例子中。
提出假设问题:
原假设 为:H0:吸烟与患肺癌没关系
备择假设为:H1:吸烟与患肺癌有关系
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
2、构造随机变量
如:在“吸烟与患肺癌是否有关系”的例子中。
构造随机变量:
K2=
(a+b)(c+d)(a+c)(b+d)
n(ad-bc)2
注:⑴不含任何未知参数
⑵K2越小,原假设H0成立的可能性越大
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
3、确定拒绝域
如:在“吸烟与患肺癌是否有关系”的例子中。
确定拒绝域: [k0,+∞)
[6.635,+∞)
注:⑴ 6.635经统计获得
⑵若原假设H0成立,则P(K2≥6.635)≈0.01
其中0.01即为显著性水平
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
4、考察临界值
如:在“吸烟与患肺癌是否有关系”的例子中。
考察临界值: k0
根据K2公式及实际数据计算K2的观测值k
k≈56.632﹥6.635= k0
不患肺癌 患肺癌 总计
不吸烟 7775(a) 42(b) 7817(a+b)
吸烟 2099(c) 49(d) 2148(c+d)
总计 9874(a+c) 91(b+d) 9965(a+b+c+d)
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
5、推断结果及解释
如:在“吸烟与患肺癌是否有关系”的例子中。
推断及解释: P(K2≥6.635)≈0.01,k≈56.632﹥6.635
观察值k落在拒绝域中,拒绝原假设,即有1-?的把握认为备择假设成立;否则接受原假设,即没有发现样本数据与原假设矛盾。(教参P108)
根据k≈56.632﹥6.635,
断定原假设:(H0:吸烟与患肺癌没关系)不成立,
即认为“吸烟与患肺癌有关系”
或者解释为:备择假设:(H1:吸烟与患肺癌有关系)成立
有99%的把握认为:吸烟与患肺癌有关系
只有1%成立的可能
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
反证法原理:
在假设一个论述不成立的前提下,如果推出一个矛盾,就证明了这个论述成立。
假设检验原理:
在假设一个论述不成立的前提下,如果一个与该假设矛盾的小概率事件发生,就推断这个论述成立。
c.反证法原理与假设检验原理
c.反证法原理与假设检验原理
反证法 假设检验
要证明的结论A 备择假设H1
在A不成立的条件下进行推理 在H1不成立的条件下,即H0成立的条件下进行推理
推出矛盾,即
结论A成立 推出有利于H1成立的小概率事件(概率不超过?的事件)发生,即H1成立的可能性(可能性为1-?)很大
没有找到矛盾,
不能对A下结论
即反证法不成功 推出有利于H1成立的小概率事件不发生,
即接受原假设
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
d. 独立性检验(假设检验的一个特例)
检验两个分类变量 x 和 y 之间是否有关系:
H0:x 和 y 之间没有关系 ←→ H1:x 和 y 之间有关系
两个分类变量 x 和 y的可能取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
e. 独立性检验知识结构图
分类变量之间关系
条形图
柱形图
列联表
独立性检验
背景分析
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
f. 教学建议
关于探究吸烟与患肺癌关系的教学建议
关于例1的教学建议
关于例2的教学建议
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
2×2列联表
关于探究吸烟与患肺癌关系的教学建议
关于探究吸烟与患肺癌关系的教学建议
通过图形直观判断,只能得到定性的结论,无法知道所得结论的可信程度及含义,因此需要用列联表检验。
关于探究吸烟与患肺癌关系的教学建议
通过图形直观判断,只能得到定性的结论,无法知道所得结论的可信程度及含义,因此需要用列联表检验。
不吸烟
吸烟
患肺癌
比例
不患肺癌
比例
推导统计量K2 用意是建立判定吸烟与患肺癌是否有关系的指标(用于构造有利于H1成立的小概率事件的指标) ,使同学了解: K2越大, H1成立的可能性就越大。
关于探究吸烟与患肺癌关系的教学建议
这种可能性的计算基于K2的分布
K2=
(a+b)(c+d)(a+c)(b+d)
n(ad-bc)2
在教学过程中强调:只有在此条件下,才能得到这个近似公式。
在教学过程中可以指出估算需要很多的概率统计知识。
在“吸烟与患肺癌没有关系”成立的条件下,可以估算出:
关于探究吸烟与患肺癌关系的教学建议
当 n→∞ 时,变为等号。在实际应用中,当
近似的效果才可接受。
结果的解释:k≈54.721>6.635解释为有99%的把握断定“吸烟与患肺癌有关” 。
若按如下规则进行判断,则把“吸烟与患肺癌没有关系”错判断成“吸烟与患肺癌有关系”的可能性不超过0.01 。
规则:若K2≥6.635,就断定“吸烟与患肺癌有关”
关于探究吸烟与患肺癌关系的教学建议
关于探究吸烟与患肺癌关系的教学建议
总结“两个分类变量独立性检验”的本质
问题:建立判断结论
H0:分类变量X与Y之间有关系
是否成立的规则。
判别指标:
规则k0:如果k>k0,判定H0成立;否则认为H0不成立。
确定规则k0判定“H0成立”犯错误的概率。
选修2-3P95表3-10给出了一些规则的犯错误的概率。
归纳两个分类变量独立性检验的基本思想:
当 很大时,就认为两个变量有关系;否则就认为没有充分的证据显示两个变量有关系。
关于探究吸烟与患肺癌关系的教学建议
在前面案例中,由 k≈54.721>6.635 可得结论:
有99%的把握断定“吸烟与患肺癌有关”。
另一方面,由 k≈54.721>10.828 还可得结论:
有99.9%的把握断定“吸烟与患肺癌有关”。
问题:二个结论矛盾吗?
关于探究吸烟与患肺癌关系的教学建议
可引导学生讨论下面问题,加深对假设检验问题的正确理解。
两个结论不矛盾,它们是对两个不同评判规则的结论。
结论“有99%的把握断定‘吸烟与患肺癌有关’”是相对于规则一:
如果随机变量的观测值大于或等于6.635就认为“吸烟与患肺癌有关系” 。
结论“有99.9%的把握断定‘吸烟与患肺癌有关’”是相对于规则二:
如果随机变量的观测值大于或等于10.828就认为“吸烟与患肺癌有关系” 。
阀值的设定
阀值的设定并无客观的标准,但目前统计学上的习惯是将其规范化到几个常用的值:最常用的是0.05,其次是0.01,0.10,更小或更大的值也可以根据情况的需要去采用。
阀值的人为性是一个常见现象,往往是为了将事务分类而不得已而做出的一种选择。
f. 教学建议
关于探究吸烟与患肺癌关系的教学建议
关于例1的教学建议
关于例2的教学建议
关于例1的教学建议
例1.秃头与患心脏病
在解决实际问题时,可以直接计算K2的观测值k进行独立检验,而不必写出K2的推导过程 。
提醒学生们注意统计结果的适用范围(这由样本的代表性所决定)。
因为这组数据来自住院的病人,因此所得到的结论适合住院的病人群体.
f. 教学建议
关于探究吸烟与患肺癌关系的教学建议
关于例1的教学建议
关于例2的教学建议
例2.性别与喜欢数学课
本例主要是使学生理解独立性检验的原理。
在教学过程中向同学们说明:在掌握了两个分类变量的独立性检验方法之后,就可以模仿例1中的计算解决实际问题,而没有必要画相应的图形。
图形可帮助向非专业人士解释所得结果;
也可以帮助我们判断所得结果是否合理
关于例2的教学建议
2020年4月21日11时23分
人教版高中数学课标教材(A版)
普通高中课程标准实验教科书选修1-2,2-3
统计案例
简 介
天津八中 陈健
欢迎光临,请多指导 2020年4月21日11时23分
两种统计方法:回归分析和独立性检验都是常用的,在统计学中占有很重要的地位。
统计方法解决问题的过程:
确定总体、选择合适变量、收集数据、分析整理数据、进行决策或预测。
数学1
数学3
数学4
数学2
数学5
选修2-3
选修2-2
选修2-1
选修1-2
选修1-1
选修3-5
选修3-4
选修3-3
选修3-2
选修3-1
选修3-6
选修4-10
选修4-9
…
选修4-3
选修4-2
选修4-1
系列1
系列2
系列3
系列4
选修
必修
数学3:
统计:随机抽样、用样本估计总体、变量间的相关关系
概率:随机事件的概率、古典概型、几何概型
选修2-3(选修1-2):
概率:离散型随机变量及其分布列、二项分布及其应用、离散型随机变量的均值与方差、正态分布
回归分析的基本思想及其初步应用、独立性检验的基本思想及其初步应用
选修4-9 风险与决策
统计学关注的是如何探知由观察数据获取的知识中的不确定性的度量,以及如何明确在最小损失下的最优决策。
教学目标
结构设置与课时分配
回归分析
独立性检验
1.教学目标
通过典型案例的探究,进一步了解线性回归模型的有关知识,包括残差变量的来源、模型诊断的初步知识、应用回归模型解决非线性相关关系问题,进一步了解回归分析的基本思想、方法及其初步应用。
b.通过典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及其初步应用。
1.教学目标
教学目标
结构设置与课时分配
回归分析
独立性检验
2. 结构设置与课时分配
统计案例
(10课时)
独立性检验模型
(3课时)
回归分析模型
(4课时)
实习作业
与小结
(3课时)
教学目标
结构设置与课时分配
回归分析
独立性检验
3. 回归分析
比《数学3》中“回归”增加的内容
回归分析知识结构图
回归分析教学建议
比《数学3》中“回归”增加的内容
必修《数学3》已学回归内容
画散点图
了解最小二乘法的思想,最小二乘估计计算公式
求回归直线方程
y=bx+a
用回归直线方程解决应用问题(进行预报)
选修《数学2-3》新增内容
引入一元线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用(异常数据识别方法、模型改进)
利用线性回归模型解决一类非线性回归问题
正确理解统计分析方法与结果
3. 回归分析
比《数学3》中“回归”增加的内容
回归分析知识结构图
回归分析教学建议
问题背景分析
线性回归模型
两个变量线性相关
最小二乘法
两个变量非线性相关
非线性回归模型
残差分析
相关指数
散点图
线性相关系数
应用
3. 回归分析
比《数学3》中“回归”增加的内容
回归分析知识结构图
回归分析教学建议
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关系数、相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
函数模型与“回归模型”的关系
函数模型:
回归模型:
样本点在函数曲线上
样本点不在回归函数曲线上
y=f(x)
y=f(x)+e
1993—2019年中国GDP散点图
函数模型与“回归模型”的关系
函数模型:
回归模型:
确定性关系
y=f(x)
y=f(x)+e
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
1):相关关系是一种不确定性关系;
对具有相关关系的两个变量进行统计分析的方法叫回归分析。
2):
注
不确定性关系
函数模型与“回归模型”的关系
函数模型:因变量y完全由自变量x确定
回归模型:预报变量y完全由解释变量x
和随机误差e确定
解释变量x(身高)
随机误差e
(其他所有变量)
预报变量y(体重)
无法得到残差变量的值,但却可以估计它,对它进行分析。
线性回归模型 见选修2-3 P83
y=bx+a+e
y=bx+a+e其中a和b为模型的未知参数,e是y与 之间的误差,通常e称为随机误差。
函数模型与“回归模型”的关系
采用最小二乘法估计模型参数:
(文科不涉及)
这样的方法叫做最小二乘法.(数学3 P92)
问题归结为:a,b取什么值时Q最小,即总体和最小.下面是计算回归方程的斜率和截距的一般公式.
根据最小二乘法和上述公式可以求回归方程.
推导过程见选修2-3 P80
为了衡量预报的精度,需要估计σ2的值?
公式中的分母取n-2是为了达到更好的估计效果。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关系数、相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
1993—2019年中国GDP散点图
散点图与模型的选择
样本点呈条状且散布在某一直线附近(线性)
在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
散点图与模型的选择
散点图帮助确定可供选择模型的范围,而模型的比较则基于残差分析
案例2:红铃虫的产卵数与温度
这些散点更像是集中在一条
指数曲线或二次曲线的附近。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
残差变量与模型选择
残差图帮助确定异常点,以及模型的改进方向。
残差图的制作及作用
在残差图中寻找异常点
可能由错误数据引起
残差图的趋势性分析
趋势性的残差图说明模型有改进的余地
?残差图的制作及作用。(选修2-3P85及教参P97)
?坐标纵轴为残差变量,横轴可以有不同的选择。
?横轴为编号,可以考察残差与编号次序之 间的关系,常用于调查数据错误。
?横轴为解释变量,可以考察残差与解释变量的关系,常用于研究模型是否有改进的余地。
?若模型选择的正确,残差图中的点应该分布在以横轴为中心的带形区域。
在残差图中寻找异常点(远离横轴)
可能由错误数据引起的异常点
异常点
异常点
身高与体重残差图
残差图的趋势性分析
残差图具有趋势性,模型有改进的余地,模型中应该添加二次项
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
残差变量的来源:
?其它因素的影响。如影响身高 y 的因素不只是体重 x,可能还包括遗传基因、饮食习惯、生长环境等因素。
?选用的回归模型近似真实模型所引起的误差。
?预报变量的观测误差。身高 y 的测量有误差。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
正确理解相关系数的含义
总偏差平方和
( , )为样本点的中心
x
y
表明两个变量之间的线性相关关系的强弱
?相关指数是度量模型拟合效果的一种指标。
?在线性模型中,它代表解释变量刻画预报变量的能力。
正确理解相关指数的含义
?相关指数是度量模型拟合效果的一种指标。
相关指数越大,模型拟合效果越好。
残差(êi)
平方和
总偏差
平方和
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
注意提炼案例所蕴含的统计思想
在例1结尾提到“用身高预报体重时,需要注意
下列问题:……”,这些论述适用于所有的回归模型。
1.模型的适用性;
2.模型的时间性;
3.样本的取值范围对模型的影响;
4.模型预报结果的正确理解。
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
1.对研究对象的背景分析;
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
某大学8名女大学生的身高与体重
确定变量:
解释变量—x(身高)
预报变量—y(体重)
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
2.利用散点图判断模型类别;
样本点呈条状分布:
身高与体重有比较好的线性相关关系,
因此可以用线性回归方程来近似刻画。
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
3.估计模型参数;
设线性回归模型:y=bx+a+e
采用最小二乘法估计模型参数:
?
=
y
-
?
b
x
(xi-
)(yi-
i=1
∑
n
)
y
x
(xi-
i=1
∑
n
x
)2
?
b
=
=0.849
=-85.712
?
y
=0.849x-85.712
x
=
1
n
i=1
∑
n
xi
y
=
1
n
i=1
∑
n
yi
注意提炼案例所蕴含的统计思想
又如教科书上所列“建立回归模型的基本步骤”,
不仅适用于线性回归模型,也适用于所有的回归模型。
1.对研究对象的背景分析;
2.利用散点图判断模型类别;
3.估计模型参数;
4.残差分析,模型诊断。
(1)根据散点图来粗略判断它们是否线性相关。
(2)是否可以用线性回归模型来拟合数据
(3)通过残差 来判断模型拟合的效果
这种分析工作称为残差分析
4.残差分析,模型诊断。
4.残差分析,模型诊断。
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差ê -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
4.残差分析,模型诊断。
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差ê -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
总偏差平方和:预报变量的变化程度
回归平方和:解释变量引起的变化程度
残差平方和:残差变量的变化程度
预报变量变化的变化之中能由解释变量引起的比例
R2越大,模型拟合效果越好。
4.残差分析,模型诊断。
回归分析教学建议
函数模型与“回归模型”的关系
散点图与模型的选择
残差变量与模型选择
解释残差变量的来源
正确理解相关指数的含义
注意提炼案例所蕴含的统计思想
应用统计方法解决实际问题需要注意的问题
应用统计方法解决实际问题需要注意的问题
通过例2,说明如下结论:
对于同样的数据,有不同的统计方法进行分析,要用最有效的方法分析数据。(残差平方和与R2)
案例2:红铃虫的产卵数与温度(残差分析)
指数模型
二次模型
残差平方和:
相关系数R2 :
1550.538
15448.431
0.98
0.80
应用统计方法解决实际问题需要注意的问题
在讲完例2通过引导学生们讨论“是不是还有其它的效果更好的模型来拟合例2中的数据?”,获得上述结论。
教学目标
结构设置与课时分配
回归分析
独立性检验
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
a. 假设检验问题
假设检验问题由两个互斥的假设构成:
原假设,用H0表示;备择假设,用H1表示。
表达式为: H0:←→ H1:
如:在“吸烟与患肺癌是否有关系”的例子中。
原假设为: H0:吸烟与患肺癌没关系
备择假设为:H1:吸烟与患肺癌有关系
这个假设检验问题可以表示为:
H0:吸烟与患肺癌没关系←→ H1:吸烟与患肺癌有关系
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
b.求解假设检验问题
考虑假设检验问题:H0←→ H1
在H0成立的条件下,构造与H0矛盾的小概率事件;
如果样本使得这个小概率事件发生,就能以一定把握断言H1成立;否则,就说从数据中没有发现充分的证据支持H1成立。
求解思路:
检验问题的解:一个规则,用以判断是H0 还是H1正确。
规则要在获取观测数据之前确定
显著性水平
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
1、提出假设问题
如:在“吸烟与患肺癌是否有关系”的例子中。
提出假设问题:
原假设 为:H0:吸烟与患肺癌没关系
备择假设为:H1:吸烟与患肺癌有关系
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
2、构造随机变量
如:在“吸烟与患肺癌是否有关系”的例子中。
构造随机变量:
K2=
(a+b)(c+d)(a+c)(b+d)
n(ad-bc)2
注:⑴不含任何未知参数
⑵K2越小,原假设H0成立的可能性越大
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
3、确定拒绝域
如:在“吸烟与患肺癌是否有关系”的例子中。
确定拒绝域: [k0,+∞)
[6.635,+∞)
注:⑴ 6.635经统计获得
⑵若原假设H0成立,则P(K2≥6.635)≈0.01
其中0.01即为显著性水平
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
4、考察临界值
如:在“吸烟与患肺癌是否有关系”的例子中。
考察临界值: k0
根据K2公式及实际数据计算K2的观测值k
k≈56.632﹥6.635= k0
不患肺癌 患肺癌 总计
不吸烟 7775(a) 42(b) 7817(a+b)
吸烟 2099(c) 49(d) 2148(c+d)
总计 9874(a+c) 91(b+d) 9965(a+b+c+d)
b.求解假设检验问题
求解过程:
1、提出假设问题
2、构造随机变量
3、确定拒绝域
4、考察临界值
5、推断结果及解释
b.求解假设检验问题
求解过程:
5、推断结果及解释
如:在“吸烟与患肺癌是否有关系”的例子中。
推断及解释: P(K2≥6.635)≈0.01,k≈56.632﹥6.635
观察值k落在拒绝域中,拒绝原假设,即有1-?的把握认为备择假设成立;否则接受原假设,即没有发现样本数据与原假设矛盾。(教参P108)
根据k≈56.632﹥6.635,
断定原假设:(H0:吸烟与患肺癌没关系)不成立,
即认为“吸烟与患肺癌有关系”
或者解释为:备择假设:(H1:吸烟与患肺癌有关系)成立
有99%的把握认为:吸烟与患肺癌有关系
只有1%成立的可能
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
反证法原理:
在假设一个论述不成立的前提下,如果推出一个矛盾,就证明了这个论述成立。
假设检验原理:
在假设一个论述不成立的前提下,如果一个与该假设矛盾的小概率事件发生,就推断这个论述成立。
c.反证法原理与假设检验原理
c.反证法原理与假设检验原理
反证法 假设检验
要证明的结论A 备择假设H1
在A不成立的条件下进行推理 在H1不成立的条件下,即H0成立的条件下进行推理
推出矛盾,即
结论A成立 推出有利于H1成立的小概率事件(概率不超过?的事件)发生,即H1成立的可能性(可能性为1-?)很大
没有找到矛盾,
不能对A下结论
即反证法不成功 推出有利于H1成立的小概率事件不发生,
即接受原假设
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
d. 独立性检验(假设检验的一个特例)
检验两个分类变量 x 和 y 之间是否有关系:
H0:x 和 y 之间没有关系 ←→ H1:x 和 y 之间有关系
两个分类变量 x 和 y的可能取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
e. 独立性检验知识结构图
分类变量之间关系
条形图
柱形图
列联表
独立性检验
背景分析
独立性检验
假设检验问题
求解假设检验问题
反证法原理与假设检验原理
独立性检验
独立性检验知识结构图
教学建议
f. 教学建议
关于探究吸烟与患肺癌关系的教学建议
关于例1的教学建议
关于例2的教学建议
不患肺癌 患肺癌 总计
不吸烟 7775 42 7817
吸烟 2099 49 2148
总计 9874 91 9965
不患肺癌 患肺癌 总计
不吸烟 a b a+b
吸烟 c d c+d
总计 a+c b+d a+b+c+d
2×2列联表
关于探究吸烟与患肺癌关系的教学建议
关于探究吸烟与患肺癌关系的教学建议
通过图形直观判断,只能得到定性的结论,无法知道所得结论的可信程度及含义,因此需要用列联表检验。
关于探究吸烟与患肺癌关系的教学建议
通过图形直观判断,只能得到定性的结论,无法知道所得结论的可信程度及含义,因此需要用列联表检验。
不吸烟
吸烟
患肺癌
比例
不患肺癌
比例
推导统计量K2 用意是建立判定吸烟与患肺癌是否有关系的指标(用于构造有利于H1成立的小概率事件的指标) ,使同学了解: K2越大, H1成立的可能性就越大。
关于探究吸烟与患肺癌关系的教学建议
这种可能性的计算基于K2的分布
K2=
(a+b)(c+d)(a+c)(b+d)
n(ad-bc)2
在教学过程中强调:只有在此条件下,才能得到这个近似公式。
在教学过程中可以指出估算需要很多的概率统计知识。
在“吸烟与患肺癌没有关系”成立的条件下,可以估算出:
关于探究吸烟与患肺癌关系的教学建议
当 n→∞ 时,变为等号。在实际应用中,当
近似的效果才可接受。
结果的解释:k≈54.721>6.635解释为有99%的把握断定“吸烟与患肺癌有关” 。
若按如下规则进行判断,则把“吸烟与患肺癌没有关系”错判断成“吸烟与患肺癌有关系”的可能性不超过0.01 。
规则:若K2≥6.635,就断定“吸烟与患肺癌有关”
关于探究吸烟与患肺癌关系的教学建议
关于探究吸烟与患肺癌关系的教学建议
总结“两个分类变量独立性检验”的本质
问题:建立判断结论
H0:分类变量X与Y之间有关系
是否成立的规则。
判别指标:
规则k0:如果k>k0,判定H0成立;否则认为H0不成立。
确定规则k0判定“H0成立”犯错误的概率。
选修2-3P95表3-10给出了一些规则的犯错误的概率。
归纳两个分类变量独立性检验的基本思想:
当 很大时,就认为两个变量有关系;否则就认为没有充分的证据显示两个变量有关系。
关于探究吸烟与患肺癌关系的教学建议
在前面案例中,由 k≈54.721>6.635 可得结论:
有99%的把握断定“吸烟与患肺癌有关”。
另一方面,由 k≈54.721>10.828 还可得结论:
有99.9%的把握断定“吸烟与患肺癌有关”。
问题:二个结论矛盾吗?
关于探究吸烟与患肺癌关系的教学建议
可引导学生讨论下面问题,加深对假设检验问题的正确理解。
两个结论不矛盾,它们是对两个不同评判规则的结论。
结论“有99%的把握断定‘吸烟与患肺癌有关’”是相对于规则一:
如果随机变量的观测值大于或等于6.635就认为“吸烟与患肺癌有关系” 。
结论“有99.9%的把握断定‘吸烟与患肺癌有关’”是相对于规则二:
如果随机变量的观测值大于或等于10.828就认为“吸烟与患肺癌有关系” 。
阀值的设定
阀值的设定并无客观的标准,但目前统计学上的习惯是将其规范化到几个常用的值:最常用的是0.05,其次是0.01,0.10,更小或更大的值也可以根据情况的需要去采用。
阀值的人为性是一个常见现象,往往是为了将事务分类而不得已而做出的一种选择。
f. 教学建议
关于探究吸烟与患肺癌关系的教学建议
关于例1的教学建议
关于例2的教学建议
关于例1的教学建议
例1.秃头与患心脏病
在解决实际问题时,可以直接计算K2的观测值k进行独立检验,而不必写出K2的推导过程 。
提醒学生们注意统计结果的适用范围(这由样本的代表性所决定)。
因为这组数据来自住院的病人,因此所得到的结论适合住院的病人群体.
f. 教学建议
关于探究吸烟与患肺癌关系的教学建议
关于例1的教学建议
关于例2的教学建议
例2.性别与喜欢数学课
本例主要是使学生理解独立性检验的原理。
在教学过程中向同学们说明:在掌握了两个分类变量的独立性检验方法之后,就可以模仿例1中的计算解决实际问题,而没有必要画相应的图形。
图形可帮助向非专业人士解释所得结果;
也可以帮助我们判断所得结果是否合理
关于例2的教学建议
2020年4月21日11时23分
